含有调和数的无穷级数恒等式

王晓元,贾利琴

(大连交通大学 理学院，辽宁 大连 116028)

0 引言

调和数的研究可以追溯到中世纪后期，它们在经典分析、数论、组合数学和计算机科学等领域中发挥着重要作用.著名的经典调和数定义如下：

其中n=1,2,…

关于调和数的一些重要性质和相关研究内容可以参看《离散数学》[1]的第六章第三节和第四节.

随着调和数研究的不断发展，数学家们给出多种广义调和数的定义形式.在过去的二十年里，含有调和数和广义调和数的无穷级数封闭求和公式不断引起人们的关注和兴趣.证明这些求和公式的方法有很多，比如：将导数算子应用于已知的二项式恒等式和终止的超几何级数等式中，Chu和De Donno证明了大量含有调和数的求和公式[2]；Boyadzhiev利用Euler变换计算了几个有限和公式[3]；Wang通过Riordan阵发现了更多新的含有调和数的恒等式[4]；De Doelder则是通过计算双伽玛函数得到大量组合公式[5].

本文设参数a和b是两个任意的正实数，定义广义调和数为

将参数a和b特殊化，得到两个重要的调和类型数

在数学文献中有很多含有上面两类数的封闭求和公式.例如欧拉在1775年发现与欧拉和有关的两个重要公式

De Doelder文献中给出下面的求和表达式[5]

最近，Chu利用Abel分部求和引理推导出几个含有调和数及变换形式的无穷级数封闭求和公式[6].本文将在此基础上，继续利用Abel方法证明几个广义调和数的无穷级数恒等式，同时得到含有经典调和数的求和公式，其中几个有趣的求和公式主要是以π2，ln2和卡塔兰常数作为结果建立的.

1 Abel分部求和引理

对于任意的复数序列{τk}，分别定义向后和向前差分算子▽和Δ为

▽τk=τk-τk-1与Δτk=τk-τk+1

(需要指出的是，在本文中的Δ与通常的向前差分算子仅相差一个负号).那么，Abel分部求和引理可表达为如下等价形式.

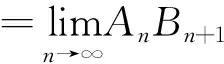
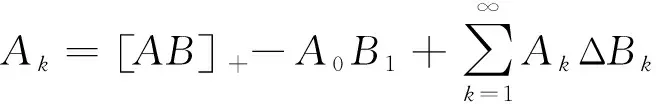
证明：根据向后差分公式的定义，我们有

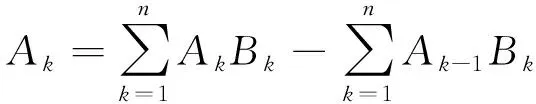
将上式中的最后一个求和指标k换成k+1，得到如下表达式

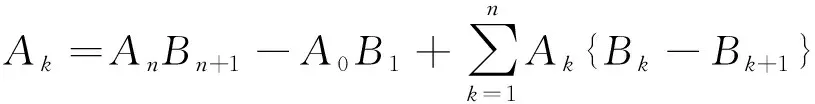
令n→∞，Abel分部求和引理得证.

2 含有调和数的无穷级数恒等式

在这一节中，我们将利用Abel分部求和引理推导涉及广义调和数的求和定理，进一步得到含有经典调和数的封闭求和恒等式.我们事先指出，本节所有的无穷级数公式中，序列{Bk}和它的向前差分取作

为了保证准确度，文中的所有公式均通过适当设计的Mathematica命令进行了数值检查.

2.1 定义如下序列{Ak}，并计算它的向后差分和极限关系

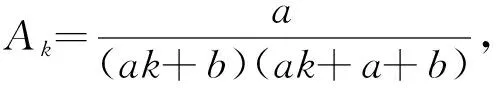
根据Abel分部求和引理，得到下述表达式

▽Ak

定理1(无穷级数求和公式)

推论1在定理1中，令a=b=1，则有

上述公式是文献[7] 中的公式(4).

推论2在定理1中，令a=2和b=1，则有

2.2 定义序列{Ak}，并计算向后差分和极限关系

根据Abel分部求和引理，得到下面表达式

用部分分式分解法计算上式右端求和式，立即可得

定理2(无穷级数求和公式)

推论3在定理2中，令a=b=1，则有

推论4在定理2中，令a=2和b=1，则有

2.3 定义序列{Ak}，同时验证向后差分和极限关系

根据Abel分部求和引理，得到下述表达式

利用部分分式法计算上式右端求和式，于是推得

定理3(无穷级数求和公式)

注意到该定理在a=b=1时，可以通过等式右端项减去左端求和第一项再取极限的方法得到下面含有调和数的求和公式.

推论5在定理3中，令a=b=1，则有

推论6在定理3中，令a=2和b=1，则有

2.4 定义序列{Ak}，并计算向后差分和极限关系

根据Abel分部求和引理，于是有表达式

利用部分分式分解法计算上式右端求和式，即得

定理4(无穷级数求和公式)

推论7在定理4中，令a=b=1，则有

推论8在定理4中，令a=2和b=1，则有

2.5 定义序列{Ak}，计算向后差分和极限关系

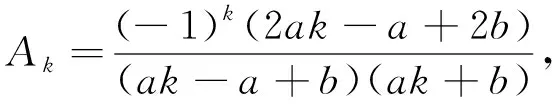
根据Abel分部求和引理，可求下面表达式

从而得到

定理5(无穷级数求和公式)

推论9在定理5中，令a=b=1，则有

推论10在定理5中，令a=2和b=1，则有

这里卡塔兰常数