转向架盖板辊弯成型工艺研究与应用

赵亚夫，李正光，郑萌，杨鑫华

(1.中车长春轨道客车股份有限公司 工程技术部，吉林 长春 130062； 2.大连交通大学 材料科学与工程学院，辽宁 大连 116028； 3.大连市轨道交通装备焊接结构与智能制造技术重点实验室，辽宁 大连 116028)*

0 引言

转向架是轨道车辆结构中最为重要的部件之一，在车辆运行中起到支撑与减震的作用.下盖板是转向架结构组成中的关键部分，是由碳钢厚板通过模具压弯或绕弯、辊弯等工艺成型.其中，模具压弯对模具精度要求极高，未解决成型工件回弹大的问题，往往需要多次模具修正才能满足工件质量要求.辊弯成型无需制作专用模具，生产成本相对其他板材成型工艺，生产成本较低，可以通过编制不同数控程序即可实现多种制件生产，节约模具制造费用；生产准备周期短，只需调试好程序即可投入正式生产，大幅缩短准备周期[1- 2].特别适合多品种、小批量、周期短制件生产[3- 4].转向架盖板具有为典型的大尺寸、超厚度工件，通用式辊弯机或滚板机均无法满足生产需求.研究中采用的辊弯成型设备为非标专用设备，其辊轮布局和通用三辊或四辊辊弯设备不同，从动辊轮的间距是固定的，传统的工艺设计计算方法不能适用于该设备[5].首件试制时，往往需要进行多次试验，才能确定出较为合理的成型工艺[6].

本文针对理论计算与有限元仿真手段，确定了S355碳钢厚板成型中的关键工艺参数，建立了实现辊弯成型工艺设计的数学模型.基于有限元仿真手段，考虑了辊弯成型中回弹对尺寸精度的影响，确定了常见尺寸下的辊弯工艺的修正参数.采用修正后的辊弯成型参数进行了典型工件试制.试验结果表明了理论公式和基于数值仿真的工艺参数修改结果的可靠性.

1 辊弯成型工艺的参数建模

长客公司目前采用的辊弯设备如图1所示，该设备包含2个主动轮和4个从动轮.在实际成型中，先由主动轮送料至一定位置，然后下压，下压完成后转到对称位置；从对称位置向上次下压方向转动，至工艺要求位置后，再实行后续下压，直至完成成型过程. 制定辊弯成型的工艺参数，主要是确定工件主动轮的下压量和工件的进给量之间的合理关系.

图1 辊弯成型设备结构图

1.1 下压量计算

如图2所示，当成型工件圆弧与两从动轮相切时，设主动轮的半径为r1，从动轮的半径为r2，成型工件的半径为R.两从动轮之间的间距为2L，板厚为t.成型完成后，主动轮圆心和从动轮的圆心距为H，主动轮的下压量为X.由于成型件与主动、从动轮均相切，根据几何关系，可以推出主动轮和从动轮的相对位置关系如式3、4所示.

图2 成型工件的圆弧与两个从动轮相切时的辊弯示意图

(1)

假设初始状态时(板材为平面)板材分别与主动轮和从动轮相切，则根据式(1)可以得到，主动轮的下压量为：

X=r1+r2+t-H

(2)

当成型工件圆弧与两从动轮不相切，而未变形部分与从动轮相切时，若辊弯区域较小，辊弯后板件的圆弧部分并不与左右辊轮相切，如图3所示.

图3 非全部圆弧时辊弯示意图

由图3可以得到：

H=(R+t+a×sinα)×cosα-(R-r1)

(3)

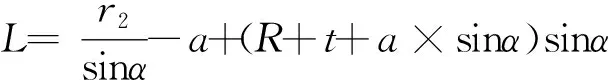
(4)

从而求得：

(5)

将式(5)代入式(3)得：

设主动轮与从动轮的初始距离为H0，则：

H0=r1+r2+t

(7)

故下压量为：X=H0-H

(8)

1.2 进给量参数的计算

辊弯时的进给量，是在主动轮的带动下板材进给量.由于板料在成型过程中，会由于弯曲成型使未成型的部分发生转动，此时以长度为度量进行进给量确定，会存在一定的困难.

假设在板料进给的过程中，主动轮和板料之间没有相对滑动，则可以用主动轮的旋转角度为度量，实现进给量的设计.在设备参数的设置时，根据角度和主动轮的半径，再推出长度方向的进给量.

设辊弯成型工件的圆弧部分的弧度角度为a，则从成型工件的一个切点到另外一个切点，主动轮的转角弧度S则为：

(9)

由于r1为定值，即100 mm，则上式可以写成：

(10)

设初始下压量为x，为保证辊弯圆弧切点为工件设计的切点位置，需要的主动轮辊弯弧度为a1，则

其中，r1=100，r2=75，L=200，则上式可化简为

(12)

上式图像如图4所示.

图4 初始下压量与主动轮转角之间的关系

因为x>0，且其值通常小于100，则式(12)可以化为：

(13)

解上式可得：

(14)

设辊弯过程经过n次下压完成，取平均每次下压量为x，则：

(15)

则主动轮第i次转角为：

(16)

2 有限元模型

2.1 材料力学性能参数

S355 钢是按照欧洲标准EN 10025生产的一种低合金高强度的结构钢.它被广泛应用于建筑、桥梁、压力容器、铁路、车辆等各个方面.特别是，随着高速铁路装备制造技术的快速发展，S355钢被大量应用于轨道客车转向架构架的制造，其屈服强度为355 MPa，抗拉强度为575 MPa，延伸率为20%， 冲击功大于20 J.

2.2 几何模型

钢板辊弯过程的几何模型如图5所示，其主要结构包括前后辊轮和两个侧辊轮.板材的几何尺寸为1 000 mm*200 mm*12 mm.主动和从动辊轮的半径分别为100 mm和75 mm，辊轮高为800 mm.

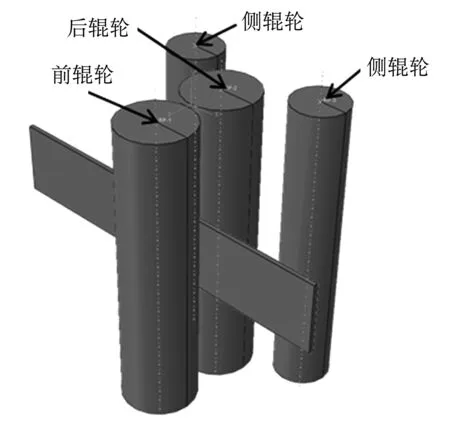
图5 辊弯成型的几何模型

3 辊弯成型工艺参数修正

第1.2章节中确定的辊弯下压量和进给量理论计算公式，并没有考虑到成型过程中板料的回弹，以及辊轮与板料之间的相对滑动问题.按照理论计算公式所确定的成型参数实现材料的辊弯成型，会由于回弹、滑动等因素，使实际成型尺寸与工件的要求成型尺寸存在差异.因此，需要对理论计算的下压量、进给量等成型工艺参数进行修正.

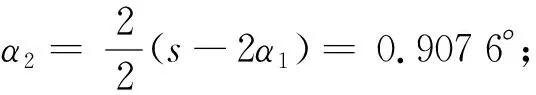
图6 成型后辊轮的相对位置

在调整前工件成型后的等效塑形应变和拟合后的成型半径如图7(a)所示.可以看出：调整前工件成型后半径为239.3 mm；基于Matlab计算得到角度150.89 mm.调整后工件成型后的等效塑形应变和拟合后的成型半径如图7(b)所示.可以看出：调整后工件成型后半径为200.01 mm；基于Matlab计算得到角度为147.09 mm.

(a)调整前

(b)调整后

图7调整前、后的工件成型效果

4 实验验证

试验在长客公司的辊弯成型机上进行.为节约试验成本，仅对直板进行辊弯成型，未按上盖板实际尺寸要求加工试件.为了验证所推导的理论公式及工艺参数修正结果的的正确性，选择T=16 mm,R=200 mm，a=147°的辊弯成型件进行辊弯试验，试验过程和成型件如图8所示.采用形状检测样板对工件进行形状测量，成形件形状误差小于0.1 mm，与仿真结果相吻合.上述验证了在转向架盖板辊弯成形中，在理论计算基础上，结合仿真对成型工艺参数进行修正的可行性与适用性.

(a)辊弯成型实验(b)成型件

图8辊弯成型实验和成型件图

5 结论

本文在系统分析辊弯成型设备和工艺特点的基础上，对其板材数控辊弯成型工艺及仿真技术开展了研究，并取得下列主要研究成果：

(1)建立了实现辊弯成型工艺设计的数学模型，推导出辊弯参数设计的理论计算公式，为实现辊弯参数设计奠定了理论基础；

(2)基于有限元数值仿真方法，考虑回弹等因素对成型尺寸的影响，在理论计算相关成型参数的基础上，对辊弯成型情况进行了仿真计算，确定了常见成型尺寸下的辊弯工艺的修正参数.