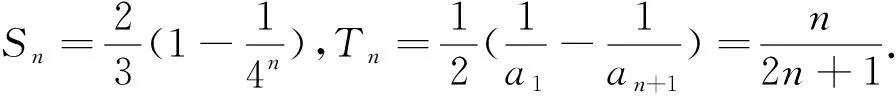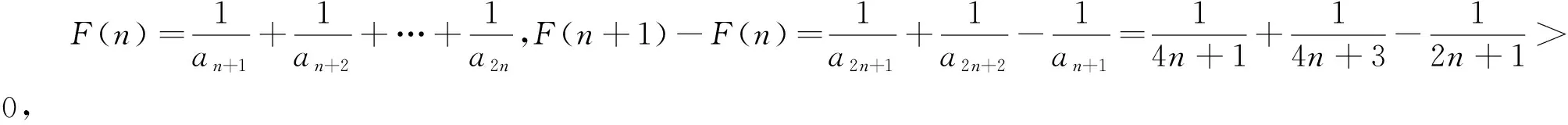抽象函数在中学数学问题解决的探讨

上海市城市建设工程学校(上海市园林学校) (200232)

章幸辛 张火明

函数是高中数学中的重要知识，抽象函数是函数知识中的一个难点，在近几年的高考上海卷、全国卷以及高中奥赛题中都高频率的出现.一般抽象函数题融函数单调性、周期性、奇偶性、定义域、值域、图像以及不等式、方程等知识于一体.通过赋值整体思考，找出一个具体函数原型等方法去探究该函数的性质，并运用相关性质去解决有关问题.在近几年高考中加大了对学生数学探究能力与创新能力的考查.

1.抽象函数的定义：那些没有给出函数的具体解析式，只给出一些特殊条件或特征的函数称为抽象函数.

2.抽象函数的背景函数：抽象函数往往都是以中学阶段所学的基本函数为背景抽象所得,解题时,若能从研究抽象函数的背景入手,由题设中抽象函数的性质,通过类比、猜想出它可能为某种基本函数，常常可以找到解题思路.当然，也有的时候并没有我们比较熟悉的函数模型，而是新定义的一种函数.抽象函数所对应的背景函数模型通常有以下几种：

抽象函数性质对应的背景函数模型f(x+y)=f(x)+f(y)-b一次函数y=ax+bf(m-x)=f(m+x)二次函数f(xy)=f(x)f(y)幂函数f(x+y)=f(x)f(y)指数函数f(xy)=f(x)+f(y)对数函数

3.一般抽象函数也可以与我们熟悉的函数，如指数函数、对数函数等一样，有自己的性质，如奇偶性、周期性、单调性等.有自己的特殊点，有自己的对称性，能画出大致图像.

4.抽象函数的解题方法一般有哪些？解题思路一般不外乎①合理赋值，化抽象为具体；②作恒等变形，找出该函数规律性、特征性特点；③分类讨论，归纳出抽象函数的实质问题.

5.典型范例

例1 已知函数f(x)在R上有定义，且满足f(x)+xf(1-x)=x.(1)试求f(x)的解析式；(2)求f(x)的值域.

例2 定义在R上的单调函数f(x)满足f(3)=log23且对任意x，y∈R,都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数；(2)若f(k·3x)+f(3x-9x-2)<0对任意x∈R恒成立，求实数k的取值范围.

证明：(1)已知f(x+y)=f(x)+f(y)(x，y∈R)①,令x=y=0，代入①式,得f(0+0)=f(0)+f(0)，即f(0)=0．令y=-x，代入①式得f(x-x)=f(x)+f(-x)，又f(0)=0，则0=f(x)+f(-x)，即f(-x)=-f(x)对任意x∈R成立，则f(x)是奇函数.

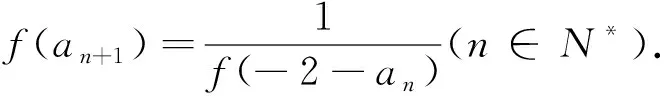
(1)求f(0)的值；

(2)求数列{an}的通项公式；

解:(1)令x=-1,y=0，得f(-1)=f(-1)·f(0)，得f(0)=1.

(2)当x>0时，-x<0，∴f(0)=f(x)·f(-x)=1，∴00，∴f(x2-x1)<1，∴1-f(x2-x1)>0，而f(x1)>0，∴f(x1)-f(x2)>0，即f(x1)>f(x2)．∴函数y=f(x)在R上是减函数．

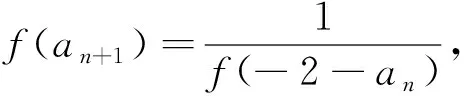
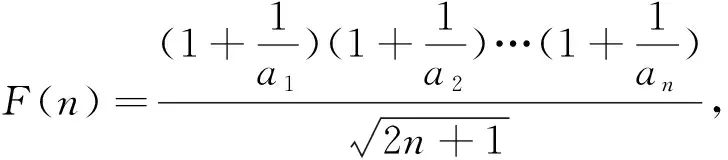
评注：从例2、例3不难看出，对抽象函数的合理赋值，对确立抽象函数的特性起着关键的作用.

解：(1)在f(a·b)=af(b)+bf(a)中,令a=b=0,得f(0)=f(0·0)=0·f(0)+0·f(0)=0.在f(a·b)=af(b)+bf(a)中,令a=b=1,f(1)=f(1·1)=1·f(1)+1·f(1),∴f(1)=0.

(2)∵f(1)=f[(-1)2]=-f(-1)-f(-1)=0,∴f(-1)=0.∴f(-x)=f(-1·x)=-f(x)+xf(-1)=-f(x),∴f(x)为奇函数.

(3)由f(a2)=af(a)+af(a)=2af(a),f(a3)=a2f(a)+af(a2)=3a2f(a),……

猜测f(an)=nan-1f(a).下用数学归纳法证明.

1°当n=1时f(a1)=1·a0·f(a)，原命题成立；

2°假设当n=k时，原命题成立，即f(ak)=kak-1f(a)，那么当n=k+1时，f(ak+1)=akf(a)+af(ak)=akf(a)+kakf(a)=(k+1)akf(a)，原命题成立.

评注：上例中，由抽象函数的关系式，找到f(an)的通项表达式，为求和奠定了基础.

例5 设y=f(x)是定义在区间[-1,1]上的函数，且满足条件：(ⅰ)f(-1)=f(1)=0;(ⅱ)对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.

(1)证明：对任意的x∈[-1,1],都有x-1≤f(x)≤1-x;

(2)证明：对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1;

(3)在区间[-1，1]上是否存在满足题设条件的奇函数y=f(x)，且使得

若存在，请举一例；若不存在，请说明理由.

证明：(1)由题设条件可知，当x∈[-1,1]时，有|f(x)|=|f(x)-f(1)|≤|x-1|=1-x,即x-1≤f(x)≤1-x.

(2)证法一：对任意的u,v∈[-1,1],当|u-v|≤1时,有|f(u)-f(v)|≤|u-v|≤1.

当|u-v|>1时,u·v<0,不妨设u<0,则v>0且v-u>1,所以|f(u)-f(v)|≤|f(u)-f(-1)|+|f(v)-f(1)|≤|u+1|+|v-1|=1+u+1-v=2-(v-u)<1.综上可知，对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1.

证法二：由(1)可得，当x∈[0,1]时,f(x)≤1-x,当x∈[-1,0]时,|f(x)|=|f(x)-f(-1)≤1+x=1-|x|.所以，当x∈[-1,1]时,|f(x)|≤1-|x|.因此，对任意的u,v∈[-1,1],当|u-v|≤1时，|f(u)-f(v)|≤|u-v|≤1.当|u-v|>1时，有u·v<0,且1<|u-v|=|u|+|v|≤2.所以|f(u)-f(v)|≤|f(u)|+|f(v)|≤1-|u|+1-|v|=2-(|u|+|v|)≤1.综上，对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤1.

(3)答：满足所述条件的函数不存在.

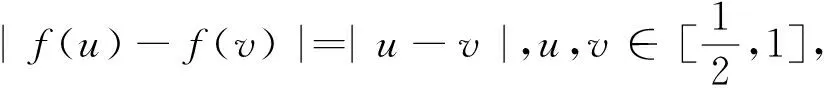
分析：这是一道利用抽象函数特性构建的数列与不等式的综合性问题.显见第(1)小问是基础，只要有了函数的解析式，后面各问均迎刃而解.

(2)①由递推关系知f(an+1)·f(-2-an)=1,即f(an+1-2-an)=f(0),从而an+1-an=2(n∈N+)，又a1=1,故an=2n-1.