巧用位置关系解决多元函数求范围问题

浙江省宁波市镇海区骆驼中学 (315202)

丁林蓬

例1 已知函数f(x)=x2+ax+b的两个零点分别在区间(0,1)和(1，2)内，求3a+2b的范围.

通常采用“线性规划”的方式解决这一问题，过程如下：

解法1:依题意可得如下可行域，

笔者认为借助直线与曲线位置关系这一观点，可以对这一问题进行这样优化的解答：

图1

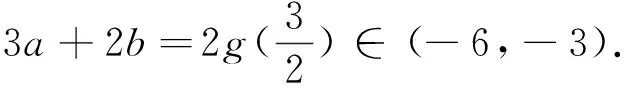
评析：解决数学问题的关键点是问题的转化——面对新的问题，通过自己的思考将其转化为某些已经解决过的数学问题.显然，这两种方法都是建立在转化的基础上展开的.

除此之外，笔者认为，解法2的“巧”体现在以下方面.

1.更加有效地避免“重复劳动”，更加方便快捷

例2 (2015浙江高考文科卷)设函数f(x)=x2+ax+b(其中a,b∈R).

(1)略；(2)已知函数f(x)在[-1,1]上存在零点，0≤b-2a≤1，求b的取值范围.

参考文献[1]中，利用“线性规划”手段给出了两种解法，现呈现一种如下：

解法1[1]：f(x)在[-1,1]上存在零点，即函数图像与x轴有交点，分有一个或两个交点进行讨论：

评析：正如原作者的点评，这一解法容易入手，想法比较自然，列出式子之后可以画出可行域，但是对作图的要求较高.

笔者认为，不仅如此，重复的绘制可行域，多次计算目标函数值，复杂的多项式都是繁琐所在.由此，笔者给出法2如下，

解法2:这一问题可以变形为-x2=ax+b，直线与二次函数所表示的抛物线分别在区间[-1,1]内有交点(条件一).令g(x)=ax+b，根据0≤b-2a≤1，得0≤g(-2)≤1(条件二)，且有g(0)=b.由此，原问题转换为：在条件一、二的前提下，计算g(0)的取值范围.

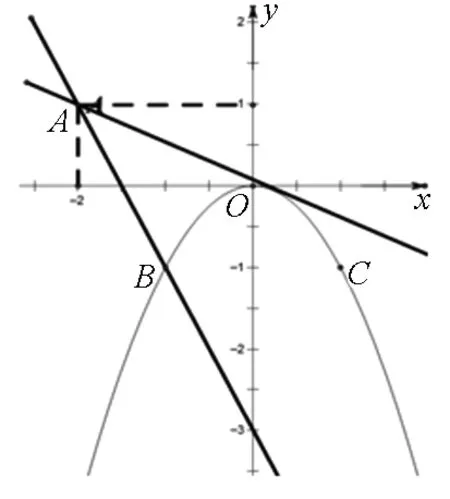
图2

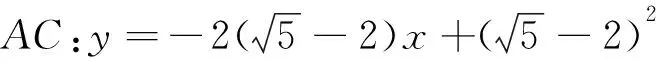
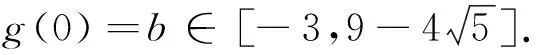
评析：这一过程更加注重思维，一定程度上使得重复、繁琐的可行域绘制过程与目标函数的求解过程得到精简，学生能够更好地触碰问题背后所蕴含的数学本质.

事实上，为了避免重复的计算过程，许多命题专家也会回避不必要的讨论，如在这一问题的条件下，2017浙江省高考数学模拟卷(考试院测试卷)，将条件强化为“在区间(0,1)内有两个零点”，解法这里不再赘述.

2.更加广泛的使用范围，更直观的视觉呈现

波利亚在《怎样解题》表中提出了“弄清问题、拟定计划、实现计划和问题解决”4个思维流程.关于计划的拟定这一过程，解题方法适用的范围越广，越容易优先被选到.下面笔者谈谈解法2相对于解法1更广泛的使用范围.

图3

例3f(x)=2ax2+2bx(其中a,b∈R).若存在x0∈(0,t)对任意不为0的a,b均有f(x0)=a+b，则求t的取值范围.

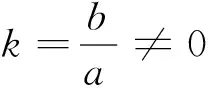
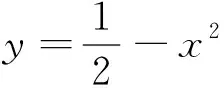
评析：显然这里运用了直线与曲线位置关系这一视角，对原始一个复杂的数学问题进行了解答.“线性规划”的手段是不能够很好地解决这一问题的，因此，这一过程充分体现了优化之后方法的使用范围之广.下面笔者再举一例.

例4 已知ex-x≥ax+b恒成立(其中a,b∈R)，试求a+b的最大值.

对这一问题，可令g(x)=ax+b，则原问题转化为ex-x≥g(x)的条件下，计算g(1).可作图4.

解法1:如图4，由于ex-x≥g(x)，因此g(x)=ax+b的“临界状态”是g(x)为y=ex-x的切线.(x0,ex0-x0)为曲线上的点，由此可得该点处的切线方程为y=(ex0-1)x-x0ex0+ex0，也即g(x)=(ex0-1)x-x0ex0+ex0，x0∈R.由此得g(1)=-x0ex0+2ex0-1=h(x0)，由导函数可得g(1)≤h(1)=e-1.

解法2:如图4，由于ex-x≥g(x)，因此g(x)=ax+b使得g(1)取最大值的“临界状态”，g(x)为y=ex-x在x=1处的切线.即g(1)=e-1.

评析：这一问题显然与线性规划问题相去甚远，其原始考查内容是导函数与函数单调性之间的关系，难度较大.显然，引入了直线与曲线的位置关系这一视角之后，原始的问题得到了直观的呈现，得以更好地认识与解决.

在一个数学问题解决之后，作为在教学活动扮演者引导者角色的教师，可以在快节奏中停下来，悟一悟.优化一些已有的数学解题方法，透过问题表面探索数学本质，这样才能更好地助力学生跨越一个又一个学习难关，不断提升逻辑推理素养.