远海风电场经VSC-HVDC联接弱受端系统的临界运行特性

边晓燕，杜中浩，魏本刚，李东东

(1.上海电力学院电气工程学院，上海 200090；2.上海市电力公司电力科学研究院，上海 200437)

0 引 言

近年来海上风电由于具有风速高且稳定、距离负荷区域近、节地环保等优势，受到各国的广泛关注[1]。按照“先近海、后远海”的风电发展原则，结合近海风电资源开发趋于饱和的现状，海上风电走向远海将是必然趋势[2]。文献[3]指出风电场距离岸边超过50km即可被定义为远海风电场，其通常选用双馈风机，经电压源变流器型的高压直流输电(VSC-HVDC)并网。远距离输电时VSC-HVDC在技术和经济上都有一定的优势，同时VSC变流器的自换相能力也使得向弱交流系统供电成为可能[4]。

目前已有风电场经VSC-HVDC并网的实际工程，如德国北海的Bard Offshore项目已于2012年投运，2016年上海也已规划了深远海风电场并入崇明弱受端电网项目。然而，双馈风机作为发电装置可以联接受端系统的强弱程度以及接入后的运行特性还有待深入研究。

现有文献大多关注两个问题：①VSC-HVDC联接弱受端系统的运行特性；②VSC变流器控制方式的不断改进。关于问题1，文献[5-6]以短路比(SCR)作为划分受端系统强弱的依据以及影响VSC-HVDC运行特性的技术指标且指出直流输电方式不能联接极弱交流系统。文献[7]从VSC接入弱受端系统的小扰动特性出发，指出接入低于临界短路比(CSCR)的极弱交流系统时，VSC变流器无法运行在整流模式。文献[8]明确了临界运行特性为交流系统同时处于临界运行状态和额定工作状态。且当直流输电系统受端是极弱交流系统时，其中设备的切换会产生很高的动态过电压，受到干扰的时候，极易发生失稳，产生诸多问题。但以上文献只是给出了临界短路比的大致范围，没有给出具体的临界值。文献[9]考虑了VSC在两种控制方式下接入弱受端系统的潮流稳定范围，并得出对应的临界短路比。文献[10]采用图解法深度分析了受端系统强度对变流器稳定运行的影响，同时检验了变流器在不同控制方式下的暂态特性，但这些结论能否运用在工程中还有待考量。关于问题②，文献[11-12]指出VSC经典电流矢量控制不适用于受端系统很弱的工况，即VSC的dq轴无法解耦，无法维持稳定运行状态。文献[13-14]分别提出了改进电流矢量控制法和功率同步控制法，可在原来的基础上有更好的控制特性。上述文献都是采用传统发电机模型来讨论VSC控制，还没有以双馈风机经VSC-HVDC联接弱受端系统的相关文献。由于双馈风机与传统发电机在运行特性和控制方式上有很多不同，需要讨论双馈风机联接弱受端系统的临界运行特性。

本文首先在DIgSILENT/ PowerFactory下建立了经VSC-HVDC的远海风电场联接弱受端系统模型，距海岸距离设为60km，通过选取双馈风机和VSC变流器控制方式，基于安全稳定运行方程，提出不断降低短路比以到达临界值的方法，同时考虑了在实际工况中阻抗角的影响。最后仿真得到不同风电场出力下的等效电抗和临界短路比，采用风速波动小干扰和暂态稳定性对其检验，为远海风电场并网工程提供理论技术依据。

1 远海风电经VSC-HVDC联接弱受端系统的数学模型

1.1 远海风电场经VSC-HVDC联接弱受端系统结构

本节研究的结构模型包括变流站、变流变压器、直流滤波器和电容器等。VSC-HVDC系统的变流站采用电压源变流器，分为风电场侧变流站(WFVSC)和电网侧变流站(GSVSC)，其简化结构图如图1所示。

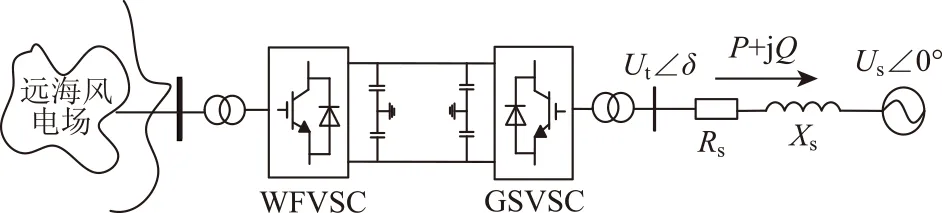
图1 基于VSC-HVDC联接弱受端系统的风电场并网结构图Fig.1 The structure diagram of the weak receiving system connected with the wind farm based on VSC-HVDC

其中，弱受端系统采用理想电压源Us与等效电阻Rs和等效电抗Xs的串联模型，以此来模拟弱受端系统的高阻抗特性；Ut∠δ为变流站和受端系统联接点处的电压(δ为Ut相对于Us的功角差)；P和Q分别表示VSC的有功和无功功率。

1.2 弱受端系统的特点

受端交流系统的强度直接关系到系统的稳定性，多数情况指对电压的支撑程度。判断指标通常用接入变流器的受端系统等值阻抗：其阻抗越小，系统结构的联系越紧密，电压波动越小，表明受端系统越强。

在模拟仿真时，常采用短路比表示系统的强弱，式(1)为其常用表达式：

(1)

式中：Sac为VSC的三相短路容量；PN为VSC-HVDC的额定传输功率；UN为直流母线的额定电压；Zs为受端系统的等效阻抗。

由于在理论计算中，交流线路的电阻相对于电抗可忽略，即当受端系统的等效阻抗角φ=90°时，若取UN为交流系统的基准电压，PN为额定直流功率的基准功率，再进一步将电抗标幺化，可得到SCR的简化表达式，如式(2)所示。

(2)

式中：XB为基准电抗；Xs.pu为受端系统等值电抗标幺值。

由(2)式可知，短路比SCR即为受端交流系统等值电抗标幺值的倒数。从广义上说，将SCR>3的系统定义为强交流系统，SCR<2定义为极弱交流系统[15]。

文献[10]借用功率圆图，阐述了受端交流系统对变流器的影响。由图2可以看出，弱受端系统需要更大范围的无功功率调节能力才能使系统稳定。

1.3 双馈风机系统数学模型

图3为双馈风力发电系统(DFIG)，和定速风机相比，其转子侧多加了一个背靠背的变流器控制，从而实现风机在不同风速下，和不同的转速下正常运行[16]。

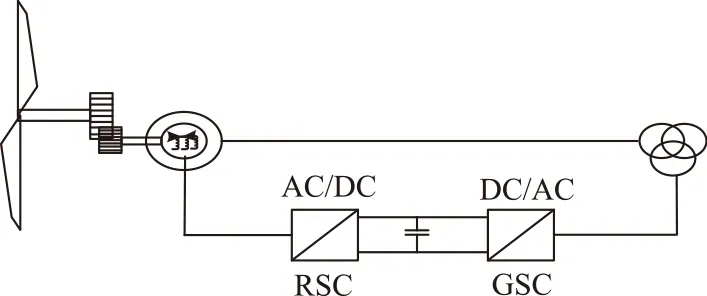
图3 双馈风机示意图Fig.3 Schematic diagram of DFIG

RSC和GSC的控制方式相似，都采用基于矢量的经典控制方式，本文通过控制定子磁链守恒来实现转子侧变流器的功率解耦，在dq轴坐标下定子侧的输出功率和定子磁链的关系式为

(3)

式中：Ps和Qs分别表示定子侧的有功和无功功率；us为定子电压；ψs为定子磁链；Lm为激磁电抗；Ls为定子自感；idr和iqr为转子的dq轴电流分量。

由式(3)可得，保持定子参数不变，通过控制idr和iqr进而实现DFIG输出功率的解耦，其简化控制框图如图4所示。

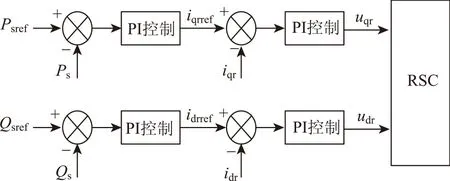
图4 转子侧变流器控制框图Fig.4 Control schematic block diagram of RSC

GSC采用电压矢量定向控制方法，其控制目标是保持直流系统电压和输出无功功率的恒定。即定义d轴方向与电网侧电压方向一致，即ed=E，eq=0，ed、eq为d轴和q轴电势，E为电网电压。则

(4)

式中：Pe和Qe分别GSC输出的有功和无功功率，其简化控制框图如图5所示。

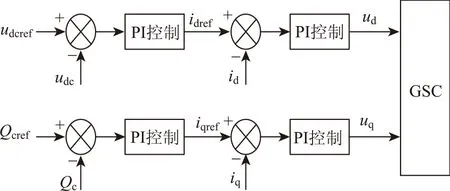
图5 网侧变流器控制框图Fig.5 Control schematic block diagram of GSC

由此可知，RSC和GSC均包含无功功率控制，使得DFIG的输出无功功率有限，相对于传统发电机，其并网后也会产生较大的无功缺额。结合在1.2小节中提到弱受端系统需要较大的无功调节范围，本文在不考虑系统无功缺额的情况下，对VSC控制和弱受端系统的临界运行特性进行研究。

2 VSC联接弱受端系统的理论分析

2.1 VSC采用定功率控制的稳定运行

在实际受端系统中，功率的频繁切换会产生损耗和系统不稳定的问题，结合双馈风机变流器控制，选用定功率控制方式使VSC的传输功率尽量保证不变。本文使用PWM控制的电压源变流器，对VSC-HVDC岸上所输出的有功功率和无功功率实现独立解耦控制，其基础控制系统图如图6所示。

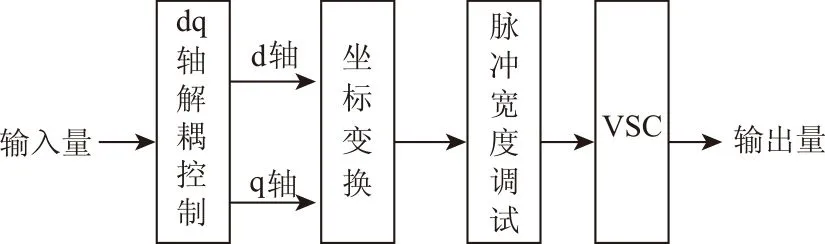
图6 VSC-HVDC 的控制系统图Fig.6 Control system diagram of the VSC-HVDC system

为简化分析过程，首先以阻抗角φ=90°的理想情况为基础，其数学模型由式(5)、(6)表示：

(5)

(6)

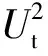
(7)

为保证受端交流系统存在潮流实数解，需要满足下列条件：

(8)

(9)

由此即可得出Ut的实数解为

(10)

同时，为保证受端系统能够稳定运行并处于安全稳定运行区域，则需要满足稳定性约束条件(11)和安全约束条件(12)，即

(11)

Ut,min≤Ut≤Ut,max

(12)

式(11)为静态电压稳定运行判据，需满足小于零的限制条件，求出零点Xsmax=0，需满足01时，VSC-HVDC的并网才不会影响到受端系统的稳定性。

式(12)中的Ut,min通常取0.95pu，Ut,max取1.05pu。

2.2 弱受端系统的临界短路比

VSC-HVDC联接弱受端系统是由电压、有功和无功判定其稳定运行点，计算临界短路比即视为不断减小VSC的短路比。由式(1)可看出，在保持额定电压一定的情况下，有两种降低SCR的方法。方法一是保持VSC-HVDC的传输功率不变，增大受端系统的等效阻抗，这也符合受端系统用户多，负荷大的特性；方法二是保证受端系统的等值阻抗一定，通过增加远海风电场的出力来提高VSC-HVDC的传输功率，这也符合远海风电机组发电的实际工况，在后文中会在仿真中验证两种方法下得到的临界短路比。

2.3 φ对CSCR影响的计算值

本小节主要是在理论计算上，分析在理想工况和实际工况下的阻抗角对临界运行状态的影响，主要是观察有功和无功的参数变化[17-18]。

当阻抗角φ=90°以及风机联接VSC-HVDC传输功率不变的理想工况下，联立与SCR的关系式为

(13)

(14)

由于sinδ<1，则若要保证VSC处于额定工作状态，需要SCR>1.5。

当阻抗角φ≠90°，即考虑阻抗角的非理想工况时，受端交流系统P和Q的函数式为

(15)

(16)

由式(15)、(16)可知，VSC-HVDC的最大传输功率Pmax和可提供的最大无功功率Qmax分别为

(17)

(18)

将最大值标幺化，并结合电压降落公式：

(19)

Us.pu=1-cosφ-sinφ

(20)

可得到Pmax.pu、Qmax.pu与SCR、φ相关的表达式(21)、(22)：

(21)

(22)

由此可得

① 取SCR=2时的广义临界短路比时，在不同阻抗角的工况下所对应的最大传输功率Pmax和所需无功功率Qmax的计算值见表1。

由表中数据可知：当无功充足时，VSC传输的最大功率随着电阻的比重加大而减小。所以对于受端系统来说，若提高VSC传输功率可以增大系统阻抗角。

② 实际工况中，当变流器不能提供足够的无功功率时，可通过加入无功补偿装置，使CSCR达到理论值。

表1 不同阻抗角下的最大传输功率与无功功率Tab.1 Maximum power and reactive power for the different impedance angles

3 VSC联接弱受端系统的仿真分析

本文通过DIgSILENT/Power Factory软件搭建了远海风电场经VSC-HVDC联接弱受端系统的模型进行仿真，模型的具体参数见表2。根据2.2小节提出的降低CSCR的两种方法，得出在不同情况下的CSCR和对应变量的关系图，并通过观察风速波动和三相短路故障对并网(PCC)点电压的仿真结果，得出结论。

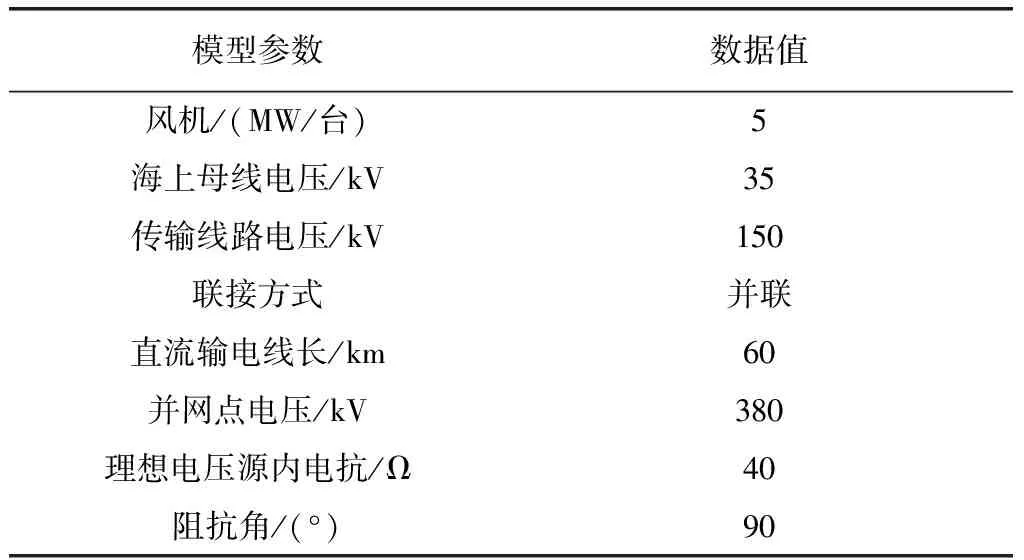
表2 模型参数Tab.2 The simulated system parameters

3.1 不同风电场出力并网的临界短路比

本小节针对提出的方法，以远海风电的接入为基础，采用递增受端系统的等效电抗控制变量法，以潮流计算存在实数解以及交流母线电压在稳定区域内波动为判断依据，得出在不同风电场出力下对应的最大等效电抗和临界短路比见表3所示，三者的图示变化情况如图7。

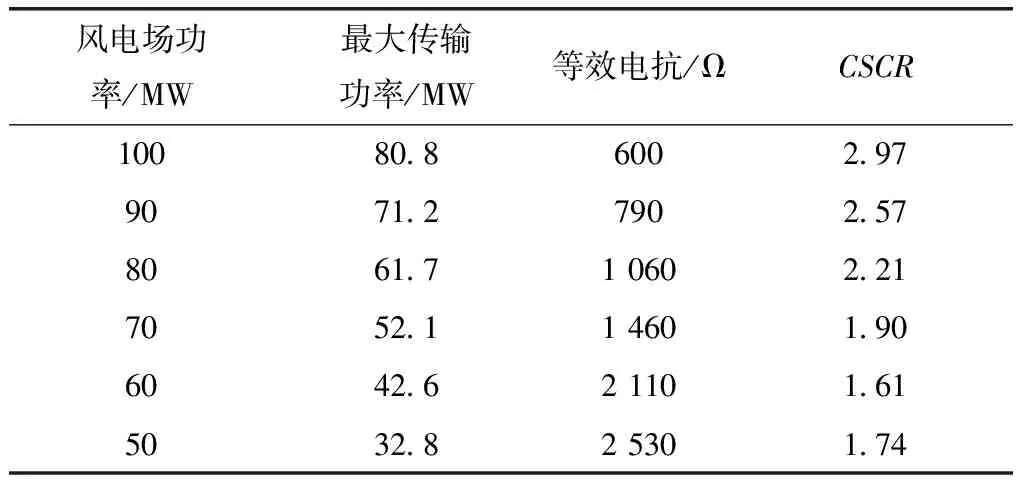
表3 不同风电出力情况下的最大传输功率和等效电抗及临界短路比Tab.3 Parameter change table maximum transferred power, equivalent reactance and CSCR under different wind power output

图7 风电场出力参数变化图Fig.7 Variations of the equivalent reactance and CSCR under different wind power output

通过仿真的结果可以看出，随着风电场出力的增多，CSCR值也随之增大，即可以接入的受端系统的强度也需要增强。其原因主要是风电场的参与会造成无功不足的情况，导致无法达到系统所能承受的最小短路比。而当风电场出力较小时，会出现母线过电压的情况，影响到受端系统的稳定性。因此图7中风电场出力和CSCR存在极值点，受端系统短路比最好大于1.6。

在实际工程中，可采取加串补电容、增加接地无功调相机和动态无功补偿装置来降低联接弱受端系统的最小临界短路比。

3.2 风速波动稳定性校验

风速波动是远海风电场运行过程中的普遍现象，当初始风速10 m/s在1s～2s内下降到7 m/s，短路比分别取1.5、1.6和1.7时，PCC点的电压波动情况如图8所示。

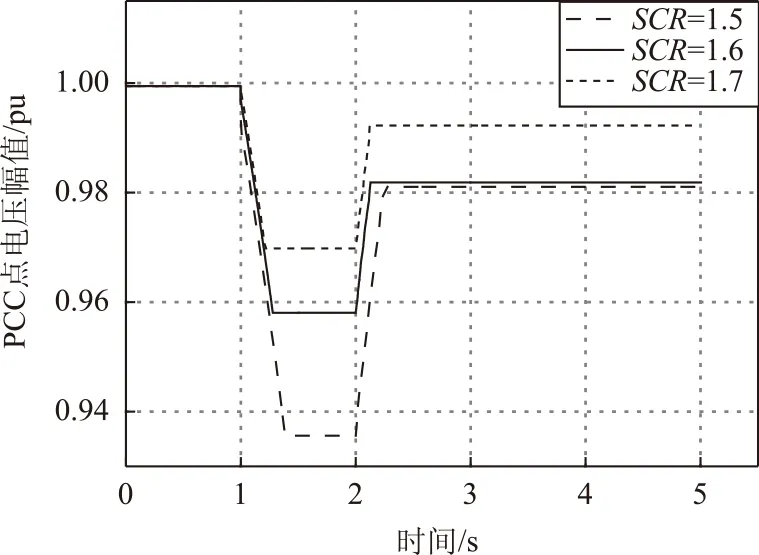
图8 不同短路比下的并网点电压Fig.8 PCC voltage of different SCR

由图8可看出，受端系统的短路比相对较大时，电压的波动较小，稳定性较好。当受端系统很弱，如图中SCR=1.5时，电压降落已低于0.95pu，系统稳定性受风速波动的影响很大。

3.3 暂态稳定性校验

在整流变流器侧母线设置三相接地短路，并在0.15s后切除故障，不同短路比对应的PCC点母线的电压变化如图9所示。

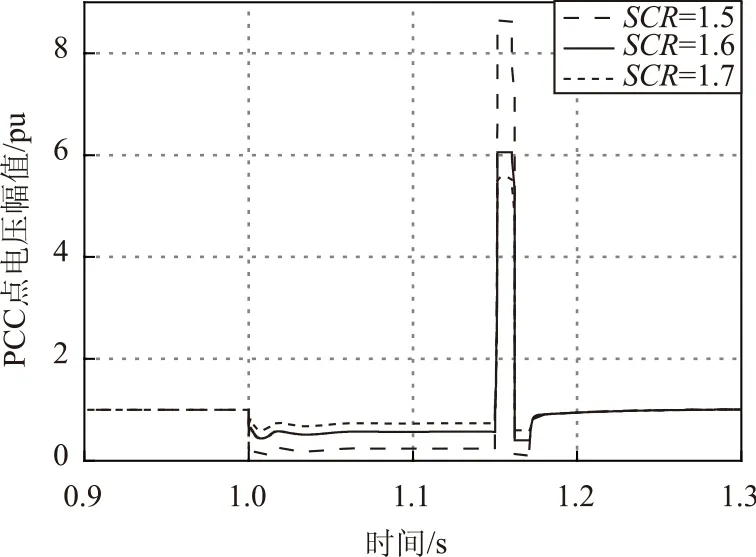
图9 不同短路比下的母线电压Fig.9 Bus voltage curves under different SCRs

当受端系统SCR为1.5时，短路故障后的暂态电压过大，恢复到稳定状态经历了较大的电压波动,而越强的受端系统暂态稳定性相对越好。

4 结论与展望

本文建立了远海风电场经VSC-HVDC联接弱受端系统的结构模型，以变流器定功率控制方式为前提，理论上分析了降低短路比的方法和阻抗角的影响。并通过仿真得到不同风电场出力下的等效电抗和临界短路比。具体如下：

① VSC-HVDC不能稳定运行在SCR低于临界短路比的极弱受端系统，而且短路比越小，则联接的受端系统越弱，对系统的稳定性威胁越大。

② 考虑到远海风电场双馈风机和弱受端系统需要更强的无功调节能力，且由于无功不足无法达到VSC-HVDC可联接的受端系统的CSCR理论值，同时考虑接入后的安全稳定运行判据，建议远海风电场经VSC-HVDC联接的弱受端系统的短路比要大于1.6。

③ 随着风电并网规模的增大，也会产生更大的无功缺额，使得系统不能提供充足的无功功率来满足弱受端系统的要求。在实际工况中，应采用无功补偿措施使该系统能够达到理论的临界短路比。