交直流混合微电网源储协同优化配置

班国邦，徐玉韬，谢百明，谈竹奎，赵武智，齐雪雯，吴家宏，吴 恒

(1. 贵州电网有限责任公司电力科学研究院，贵州贵阳 550002；2.贵州电网有限公司电力调度控制中心，贵州贵阳 550002；3.北京四方继保自动化股份有限公司，北京 100085)

0 引 言

微电网集成风电、光伏、生物质能等可再生能源与石油、天然气等化石能源以及电池、超级电容器等储能系统(energy storage system, ESS)，具有多源惯性供能、多模式协调运行特点[1-2]，可充分发挥分布式电源技术优势，有效提高电力系统可再生能源接纳比例，从而缓解由化石能源日益消耗所带来的环境污染和能源短缺问题[3-6]。

微电网的组网方式包括交流微电网、直流微电 网和交直流混合微电网[7]。其中，交直流混合微电网兼顾交流与直流微电网的特点与优势，既可降低多重AC/DC或DC/AC变换所产生的功率损耗与谐波电流，也为各种类型的可再生能源与用电设备提供多样的接入方式选择。其主要特征如下：①交直流混合微电网包含交流子系统、直流子系统以及交直流子系统间的双向AC/DC变换器，交直流子系统间功率可双向流动；②交直流混合电网可直接供应交流负荷和直流负荷，减少电能转换中间环节；③相比于单纯的交流微电网或直流微电网，交直流混合微电网可更好地接纳不同类型的分布式电源、储能单元，提升系统电能质量和经济性。

为充分利用具有间歇性出力特性的分布式电源，同时保证电网稳定性与用户用电可靠性，需要在微电网内合理配置储能系统[8-9]。与此同时，微电网内用户负荷增长又促使微电网内须不断增加新的分布式电源以满足用电需求。文献[10]从能量管理策略的角度，对交直流混合微电网中分布式电源进行优化配置，以降低系统运行成本，但是文中仅考虑了微电网独立运行模式。文献[11]针对并网型交直流混合微电网提出了多目标优化配置方法，采用第二代非支配排序遗传算法求解，求取在不同直流负荷水平下交直流混合微电网的最优配置。文献[12]以经济成本最小和联络线利用率最大为综合目标对并网型微电网中的蓄电池和超级电容混合储能系统进行储能容量优化。文献[13]针对并网型交直流混合微电网中的分布式电源提出了选址定容方法。

然而，分开配置电源与储能系统无法协同考虑电源与储能系统的时序动态特性，从而无法达到电源与储能系统的最优配置。另一方面，交流微电网与直流微电网混联后，可相互作为备用，相互支撑，同时需要考虑交直流联络线传输功率极限与功率损耗。为此，本文提出交直流混合微电网源储协同优化配置模型，以实现更经济的源储配置方案。

1 交直流混合微电网

1.1 交直流混合微电网结构

如图1所示，交直流混合微电网由交流子系统与直流子系统组成，包含双向AC/DC变换器、集中控制器、并网接口单元、常规电源、风电、光伏等可再生电源、储能单元和交/直流负荷。

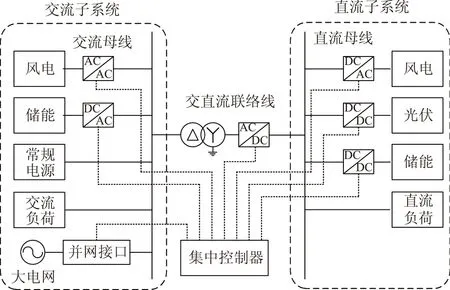
图1 交直流混合微电网结构图Fig.1 The structure of hybrid AC/DC microgrid

微电网与大电网功率传输pm(t)与交直流子系统功率传输pl(t)方向定义如下：

1.2 交直流混合微电网运行策略

针对上述交直流混合微电网，本文采用如下运行策略：可再生能源(如风电和光伏)优先向系统供电。控制光伏电池板和风力发电机实现最大功率点跟踪(maximum power point tracking, MPPT)。当直/交流子系统可再生能源出力超过直/交流子系统负荷时，优先将剩余功率转移到交/直流子系统，保证可再生能源优先消纳。当可再生能源仍无法全部消纳时，通过储能系统储存剩余电量。

储能运行策略则相应为：在储能荷电状态(state of charge, SOC)满足上下限值要求的前提下，当整个系统内剩余可再生能源时，储能充电，对剩余的可再生能源进行存储，以满足可再生能源最大出力要求。当整个系统内可再生能源出力不足或者常规电源爬坡能力不足时，储能放电，配合常规电源一起满足负荷需求。

当采用上述策略仍无法使网内源储荷达到平衡时，则向大电网购电或售电，以平抑不平衡功率。

2 源储协同优化配置模型

在交直流混合微电网中，交流子系统通过并网接口单元与大电网相连，交直流子系统通过交直流联络线与双向AC/DC变换器互连。在计及交直流联络线功率的情况下，综合考虑储能电池动态时序特性、常规电源动态时序特性、负荷动态时序特性、微电网内交流子系统功率平衡、直流子系统功率平衡和交直流联络线功率约束，构建如下源储协同优化配置模型。

2.1 目标函数

2.1.1 投资成本最小

微电网源储投资成本包括电源投资成本与储能投资成本，可表示为

mincgx+csy

(1)

式中：x为整数，表示常规电源建设数量;cg为电源单位建设成本；y为整数，表示储能电池建设数量;cs为储能电池单位建设成本。

2.1.2 运行成本最小

微电网运行成本包括发电成本与购售电费用，可表示为

(2)

式中：pg(t)为t时刻常规电源出力;f(pg)为常规电源发电成本函数，其通常为二次函数，可转化为分段线性函数;pres(t)为t时刻可再生能源出力;g(pres)为可再生能源发电成本函数;pm(t)为t时刻大电网与微电网交换功率;cm(t)为t时刻微电网向大电网购/售电电价。

2.2 储能时序动态特性

本文分别使用充电功率和放电功率两个变量来描述储能充放电过程，由于充放电过程存在损耗，所以优化模型可保证储能电池充电与放电不会同时发生。储能电池充放电过程如图2所示。

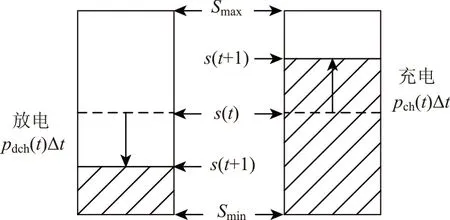
图2 储能充放电过程Fig.2 The charging/discharging process of storage

考虑储能电池充放电效率，其充放电过程可表示为

s(t+1)=s(t)+pch(t)Δtβch-pdch(t)Δt/βdch

(3)

式中：s(t)与s(t+1)分别为t时刻与t+1时刻储能电池的荷电状态;pch(t)、pdch(t)分别为t时刻储能电池的充电功率与放电功率;βch、βdch分别为储能电池的充电效率与放电效率;Δt为单位时间间隔，通常设定为1h。

储能电池在充放电时不应超过其最大充放电功率

pch(t)≤Pch,max

(4)

pdch(t)≤Pdch,max

(5)

在运行过程中，为避免损伤储能电池，其荷电状态须保持在上下限范围内：

y×Smin≤s(t)≤y×Smax

(6)

式中：y为储能投资决策;Smax、Smin分别为储能电池所能储存电量的上下限。

经过一个完整的时间周期(如一天)，储能电池荷电状态应回到初始值，如图3所示。

s((n+1)T)=s(nT)

(7)

式中：T表示一个完整周期;n为自然数。

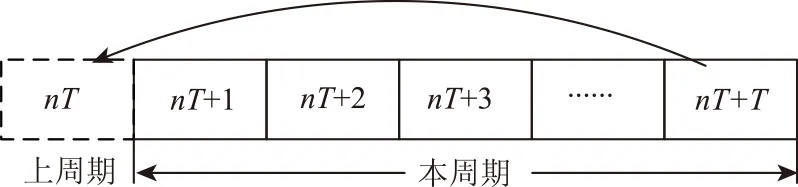
图3 储能电池周期Fig.3 The charging cycle of storage

2.3 电源时序动态特性

对于常规电源，其出力上下限约束为

x×Pmin≤pg(t)≤x×Pmax

(8)

式中：x为常规电源投资决策;Pmax、Pmin分别为常规电源出力上下限。

为适应可再生能源间歇性出力并满足负荷峰谷要求，其爬坡速率需要满足一定范围

Pdown≤pg(t+1)-pg(t)≤Pup

(9)

式中：pg(t)与pg(t+1)分别为t时刻与t+1时刻储能电池的荷电状态;Pup、Pdown分别为爬坡速率上下限。

2.4 功率平衡约束

令pl为交直流联络线功率(以交流侧为基准)，其正方向为交流子系统流向直流子系统。图4为交直流子系统功率传输示意图。

图4 交直流子系统功率传输示意图
Fig.4 The sketch of power transfer between AC and
DC subsystem

考虑交直流联络线功率传输效率

α

，则交流侧功率传输、直流侧功率传输可分别表示为

(10)

式中：δ(·)为阶跃函数，输入变量大于等于0时函数值为1，输入变量小于0时函数值为0。

对于交流子系统，其功率平衡方程为

pg(t)+pres(t)+pdch(t)+pm(t)=

pch(t)+pd(t)+pac(t)

(11)

对于直流子系统，其功率平衡方程为

pg(t)+pres(t)+pdch(t)+pdc(t)=pch(t)+pd(t)

(12)

式中：pg(t)为t时刻常规电源出力;pres(t)为t时刻可再生能源出力;pch(t)、pdch(t)分别为t时刻储能电池充电功率与放电功率;pm(t)为t时刻大电网流入交流子系统功率;pd(t)为t时刻负荷。

2.5 联络线功率约束

大电网向微电网输送功率应满足上下限约束

|pm(t)|≤Pm,max

(13)

式中：pm(t)为t时刻大电网向微电网输送的功率;pm,max为传输功率上限。

交直流联络线传输功率应满足上下限约束

|pl(t)|≤Pl,max

(14)

式中：pl(t)为t时刻交直流联络线功率;pl,max为联络线功率上限。

3 求解算法

式(1)至式(14)可以归结为一个混合整数线性规划(mixed integer linear programming, MILP)问题，其矩阵形式如式(13)至(15)所示

(15)

Ax+By+Cz≥d

(16)

Gx+Hy+Mz=h

(17)

式中：z为所有运行变量所构成的列向量，包括常规电源出力pg(t)、储能电池荷电状态s(t)、充电功率pch(t)、放电功率pdch(t)、大电网注入功率pm(t)、交直流联络线功率pl(t)。

其中，目标函数式(15)由式(1)和(2)构成，式(16)表示不等式约束(4)～(6)、(8)～(9)、(13)～(14)，式(17)表示等式约束(3)、(7)、(11)和(12)。为提高MILP求解速度，通常可采用Benders分解[14]算法分层迭代求解。本文基于Benders分解算法求解上述MILP，在保证全局最优解的条件下获得更快的求解速度。

基于Benders分解算法的分层计算思路，可将整数问题分为上层问题，连续变量问题分为下层问题。其中上层问题为

(18)

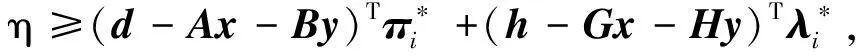
(19)

基于对偶理论，下层问题可表示为

max(d-Ax*-By*)Tπ+(h-Gx*-Hy*)Tλ

(20)

CTπ+MTλ=b

(21)

π≥0

(22)

式中：η为上层问题松弛变量;λ和π分别为约束(16)和(17)所对应的对偶变量。

求解步骤如下：

① 令迭代次数k=0，上边界UB=+∞，下边界LB=-∞。

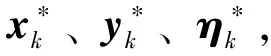
④ 如果UB-LB≤ε，算法终止，否则继续下一步。

⑤ 在主问题的松弛问题中加入如下约束，返回步骤②。

(23)

式(23)即为Benders分解算法的最优割。在实际计算中，在下层问题加入罚项，从而可以保证下层问题存在最优解，因此可以省略可行割[15]。

4 算例分析

4.1 算例系统

在图1所示交直流混合微电网结构下，各电源和储能根据其出力性质分别接至相应母线，向交直流负荷供电。燃气轮机作为常规电源接入交流子系统，风机接入交流子系统，光伏与储能电池接入直流子系统。交流、直流负荷分别接入交流、直流子系统。取单位时段Δt为1h，电池运行周期为1天。本文研究的电池储能采用的是GEFC公司生产的125V200A-VRB型全钒液流电池堆，单台储能容量为50kWh。表1给出了系统各参数，表2给出了大电网与微电网交易的分时电价。

本文选取4组典型日场景以考虑风电、光伏、交直流负荷的随机特性。风电日出力曲线、光伏日出力曲线、交直流日负荷曲线如图5所示。4组典型日数据均从实际运行数据中抽取，其幅值经过适当处理以适应本文算例系统。场景1中，风电出力低且平稳，光伏出力高且波动性最大；场景2中，风电出力高、波动性较小，光伏出力较高，可再生能源出力充裕；场景3中，风电出力具有明显反调峰特性，即负荷低谷期风电出力高，负荷高峰期风电出力低，光伏出力较低；场景4中，风电出力昼高夜低，波动性最大，光伏出力最低。图5(c)为上述4个场景所对应的交直流负荷曲线，其中实线代表交流负荷，虚线代表直流负荷。

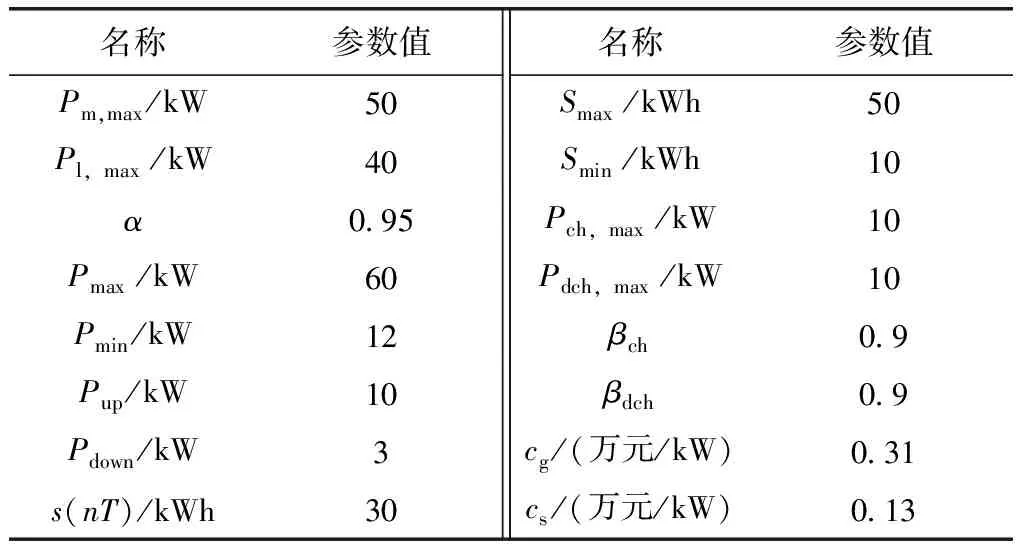
表1 系统参数

表2 电网分时电价 元/kWh

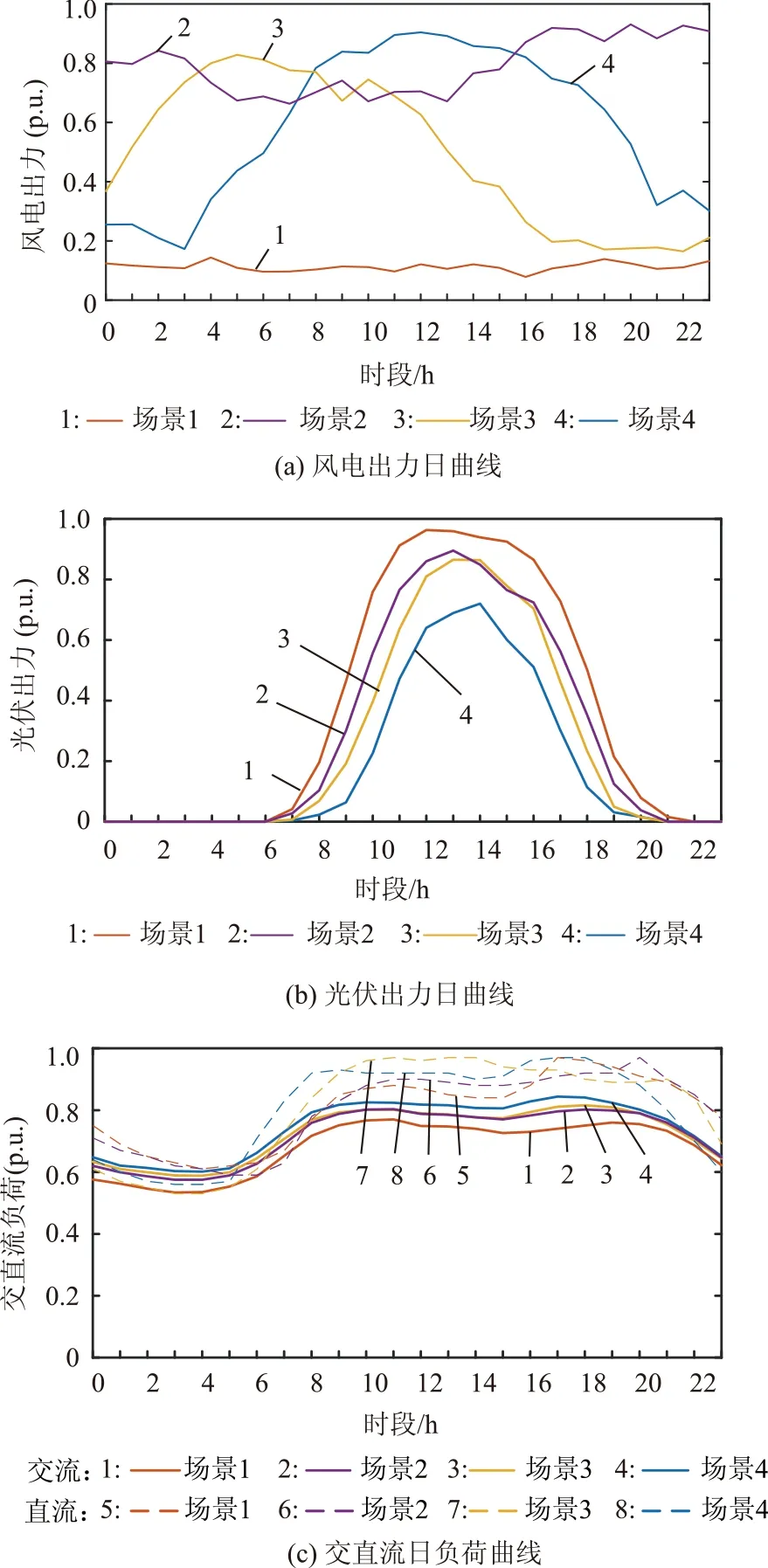
图5 可再生能源出力与负荷曲线Fig.5 The profile of renewable energy resources and load

4.2 算例结果

表3给出了3类方案下的交直流混合微电网优化配置结果，方案1和方案2分别为电源与储能分开配置，方案3为电源储能协同优化配置。

表3 交直流混合微电网优化配置结果

由表3可知，当仅考虑电源投资或者储能投资时，其投资成本分别为74.4万元和58.5万元，运行成本为102.9万元和137.1万元。当电源与储能协同配置时，其投资成本为69.7万元，运行成本为93.8万元。显然，在3个方案中，方案2的投资成本最低，但是加上运行成本后，方案2总成本达到195.6万元，成为经济性最差的方案。这表明仅考虑储能投资建设虽然可有效接纳可再生能源、满足负荷峰谷要求，但是过度依赖于向大电网购电，使得运行成本过高。对比方案3和方案1，方案3投资成本较方案1节省了4.7万元，运行成本较方案1节省了9.1万元，因此，源储协同配置可有效节省电源投资建设费用，并提升交直流混合微电网运行经济性。

图6给出了在方案3下单台电源出力与单台储能荷电状态的时序曲线。图5与图6是时序对应关系，结合图5与图6可以进一步观察4个典型日场景中电源出力与储能充放电的运行情况。

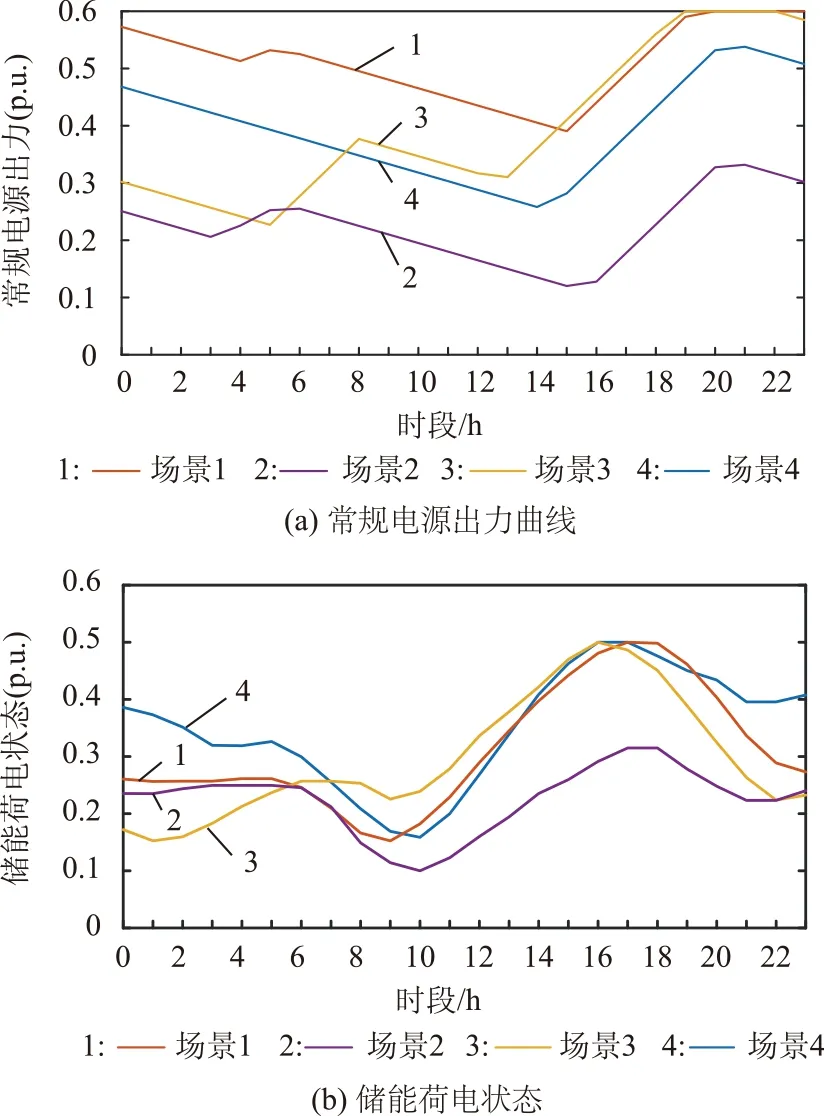
图6 电源及储能运行特性曲线Fig.6 The profile of generation and storage operation

风电出力全天波动性较大，光伏出力集中在白天，呈单峰特性，负荷则呈现双峰特性。在0:00-6:00时段，风电出力波动较大，且各场景间无明显规律，光伏无出力，系统内负荷较低随时间呈递减趋势，此时由常规电源与储能联合调节以满足风电消纳和负荷需求。6:00—10:00时段，负荷上升明显，尽管此时光伏出力也在上升，但仍无法满足负荷需求，需要储能放电。10:00—16:00时段，光伏出力达到峰值，常规机组下调出力，在满足负荷需求时，同时给储能充电。在16:00—20:00时段，负荷仍较高，但此时光伏出力快速下降，风电出力也有不同程度下降。可以看出，该时段是系统调峰最困难的时段，需要常规电源迅速上调出力同时储能放电才能满足负荷需求。此外，从4组储能荷电状态曲线中可以看出，荷电状态都回到了初始值。在4组典型日中，可再生能源全部消纳，子系统间实现了能源互补，常规电源与储能平抑了系统不平衡功率，满足了系统调峰需求。

5 结束语

针对交直流混合微电网，本文综合考虑电源储能的时序动态特性与交直流联络线功率传输极限与损耗，建立了交直流混合微电网源储协同优化配置模型，得到以下结论：

① 本文提出的交直流混联微电网源储协同配置模型，考虑了电源与储能的时序动态特性，并计及交直流联络线功率传输损耗，可以得到有效的源储配置方案。

② 通过本文算例分析，与单独规划电源与单独规划储能相比，源储协同配置方案可以节省总成本约13.8～32.1万元，可有效提升系统经济性。

③ 本文构建了交直流混合微电网的混合整数线性规划模型，并基于Benders分解算法的数学优化方法求解，可保证得到全局最优解。

需要指出的是，本文未能计及储能电池容量随充放电循环次数增多而递减的特性。另外，所研究的交直流混合微电网仅为两个微电网互联。下一步可考虑将多交直流微电网混联作为研究对象，同时计及储能系统的衰减特性。