配电网故障时空特征及形成机理分析

王建雄，肖麟祥，唐海国，刘海峰，马 瑞

(1.国网湖南省电力公司，湖南长沙 410007；2.长沙理工大学电气与信息工程学院，湖南长沙 410114;3.国网湖南省电力公司电力科学研究院，湖南长沙 410007)

0 引 言

随着国民经济的飞速发展，全社会对电能的需求量不断增长。与此同时，电网规模也不断扩大，复杂程度不断提升[1]，配电网作为电力网络中与用户直接相连的部分，其安全可靠性影响着人们的日常生活和工作。对配电网的故障统计分析是电网可靠性分析的重要组成部分。

许多学者对电网故障分布特性及其形成机制进行了研究：文献[2-3]通过统计我国东北、西北、华中、南方电网发生的重大停电事故，得出大停电事故的自组织临界特性是客观存在的；其中文献[3] 加入小棍机制、减少故障传递和主动解列3种控制规则发现新的幂律函数在双对数坐标下斜率有所增加，降低了大型事故发生的概率。进一步地，文献[4]对输电网故障进行分析研究，表明电网故障和大停电事故一样，在时间上近似满足幂律分布且具有比较强的长程正相关性,其Hurst指数约为1；同时，文献[5]从空间层面统计了H省500kV输电线路故障次数与其发生频次和累计概率的关系，为电网的风险管控提供了辅助决策的依据。上述研究表明，处于临界状态下的输电网故障后线路潮流的大规模转移和继电保护的不恰当动作是触发连锁故障[6-8]，使输电网故障具有幂律特征的直接原因。而配电网中一般采用开环运行方式，线路故障后首先进行定位，再执行倒闸操作，最后恢复供电，由潮流转移导致的连锁故障概率较低。因此，文献[9-11]分别对濮阳、南昌和张家界等地的配电网故障展开研究，发现其在时间序列上也具有类似输电网的幂律分布特性，并给出了极端天气所致的合理解释。文献[12]应用数据分析方法对配网停电时户数和停电持续时间两个可靠性指标进行统计分析，初步验证了配电网停电事故的自组织临界特性。以上文献均未从空间上对配电网故障的分布特性及其形成机理展开研究，同时由于配电网网架结构复杂，对其进行多时间尺度和多空间尺度的对比分析，能够更好地反映出配电网的敏感时期和薄弱环节。

为此，本文以H省各地级市配电网为例，收集了2016年7月～2017年6月的配电网故障数据，首先在时间上以日故障次数为单位，在空间上以配电网故障所在线路为单位分析统计其分布特性；然后从多时空角度出发统计其周故障次数、月故障次数，并从客观角度分析了其在时间和空间上所服从分布的形成机理；最后将各地级市配网故障分布特性在同一坐标下进行了对比分析验证。

1 配电网故障特征及其分析方法

1.1 配电网故障特征

H省属大陆性亚热带季风湿润气候，气候年内变化较大。冬寒冷而夏酷热，夏秋少雨，秋冬干旱，夏季年平均气温大都在27℃～29℃，日最高气温≥35℃的酷热天数达到一个月以上，电网故障多发生在夏冬两季。

本文基于H省配网抢修指挥应用平台统计了H省配电网2016年7月～2017年6月所有归档后的故障停电抢修工单信息，原始数据中记录了市公司、供电所、主线名称、支线名称、台区名称、台区编号、故障原因、故障时间和故障修复时间等。本文共统计了近64 000条抢修工单信息，覆盖面达到14个地市公司，656个供电所，28 694个台区。

全省不同的停电事故所占比例如图1所示。

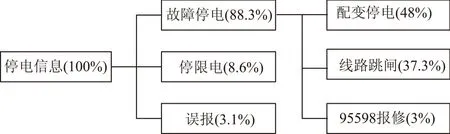
图1 停电事故原因统计Fig.1 Power supply blackout causes statistics

从图1中可以看出，计划停电和误报占到了总停电事故的11.7%，由于其并非真正意义上的故障停电，不在本文统计范围之内。配电网故障停电可以分为主线跳闸、支线跳闸和配变停电，线路跳闸和配变停电共占到了配电网总故障停电的88.3%，所以本文主要考虑线路跳闸和配变停电在多时间尺度和多空间尺度上的分布特征。

1.2 配电网故障数据的研究方法

一方面，经典可靠性理论认为：输配电线路、变压器等一次设备元件的故障失灵事件可以用泊松分布描述，元件失效事件之间相互独立，由这样的多个元件组成的电网在单位时间内发生的故障次数具有指数分布规律[11-13]。

指数分布的累积概率函数可表示为

P(X≤x)=1-e-λx

(1)

移项后两边取双对数，得

lg[P(X>x)]=-λx

(2)

可见指数分布在单对数坐标下呈斜率为λ的直线状。

另一方面，根据分形理论，如果某客体的标度r和标度的频度或概率P满足关系式(3)，则可以说该客体具有分形结构(服从幂律分布)，即

P=cr-D

(3)

式中：c为待定参数；D为分形维值，即幂律值。

将式(3)两边取常用对数进行双对数变换，得

lgP=lgc-Dlgr

(4)

利用上式对配电网故障时空特征进行分析时，标度r为日、周、月故障次数或者台区、线路的故障次数；P为出现的频度或者概率。

2 配电网故障时空特征分析

2.1 配电网故障时间特性分析

本文所用数据来源于用电信息采集系统归档后的抢修工单，考虑到个别城市配电自动化程度不高，运行数据尚未全部接入配网抢修指挥平台，本节以A市为例分析配电网故障时空特征。

表1列出了A市日故障次数的标度-频率统计结果。根据分形理论的无标度特性，表1中仅列出了部分标度及其频率。

表1 A市2016～2017年配网日故障次数Tab.1 Daily failure number statistics of the distribution network in A city

利用CFtool拟合工具箱在双对数坐标下对日故障次数的标度和概率进行拟合，结果如图2所示。

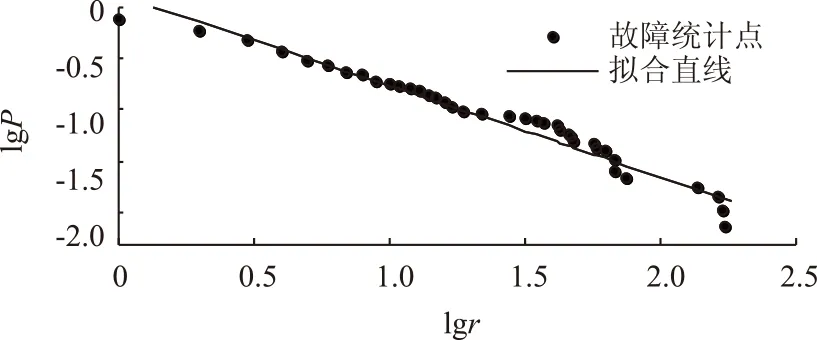
图2 双对数坐标下日故障次数的累积概率密度Fig.2 Cumulative probability density distribution of daily failure number on the double logarithmic coordinates

拟合得到的线性相关关系为

lgP=0.485 2-1.027lgr

(5)

式中：r为选定的标度;P为日故障次数的累积概率。

可见日故障次数及其累积概率密度在双对数坐标下呈直线。对拟合结果进行检验，决定系数R2为0.941 4，标准误差RMSE为0.133 6，拟合效果较好，认为lgP和lgr线性关系显著。因此配电网日故障次数在时间上近似服从幂律分布。

2.2 配电网故障空间特性分析

对A市配电网2016年7月～2017年6月内的配变故障和主线跳闸以其所在主线为分类标准进行统计，记录该主线跳闸或该主线下台区发生的配变停电。表2中列出了以主线为统计单位的线路跳闸和配变停电故障次数及其频率的部分数据。

在双对数坐标下绘制的配电网故障空间统计特性及其拟合直线如图3所示。分布关系近似为

lgP=0.498 8-1.716lgr

(6)

式中:决定系数为0.963 8;标准误差为0.149 7。

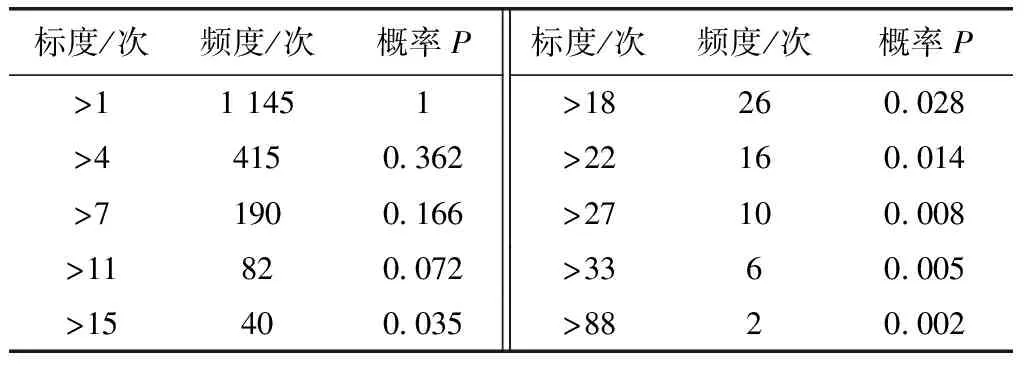
表2 A市2016～2017年配网主线下故障频率统计Tab.2 Fault frequency statistics under bus from 2016 to

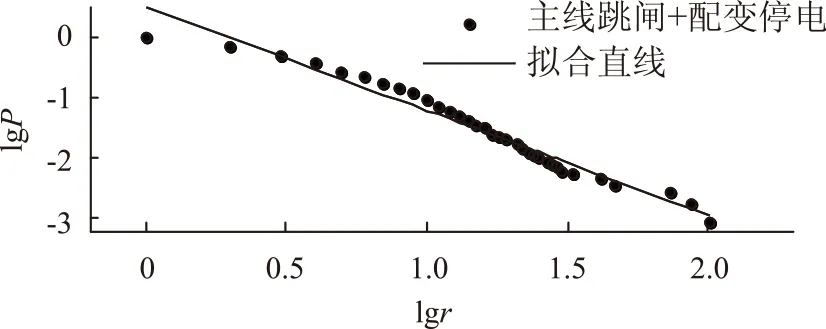
图3 双对数坐标下故障所属主线故障次数的累积概率密度Fig.3 Cumulative probability density distribution of key buses failure number on the double logarithmic coordinates

由图3可知，A市配电网故障所属主线及其累积概率在双对数坐标下呈直线，且拟合效果较好，因此配网故障在空间上也近似满足幂律分布。从表2中可得线路下辖台区年故障次数在22次及以上的仅为1.4%，大部分的线路下辖台区年故障次数为3次以下，整个配网相对来说较坚强。

2.3 多时空尺度下故障特性分析

根据分形理论可知，分形具有任意尺度意义下的自相似性和标度不变性。在上述表1—图2，表2—图3的转换过程中，标度不变性已经得到了验证。下面将分析其自相似性。

在不同的时间尺度下对A市的故障次数进行时间特性分析，分别以周故障次数和月故障次数r的常用对数为横坐标，以累积概率密度P的常用对数为纵坐标得到的拟合图如图4所示。

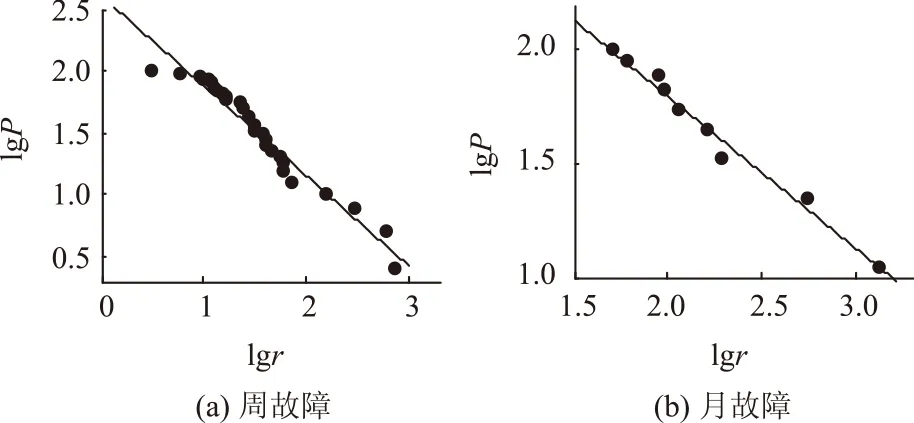
图4 双对数坐标下多时间尺度故障次数累积概率密度Fig.4 Multi-time cumulative probability density distributions of failure number on the double logarithmic coordinates

以故障所属台区和故障所属线路两个不同的空间尺度为统计单位统计配变停电的停电次数及其累积概率(以台区为统计单位时，无法统计线路跳闸故障，所以只统计配变停电故障)，在双对数坐标下的拟合图如图5所示。

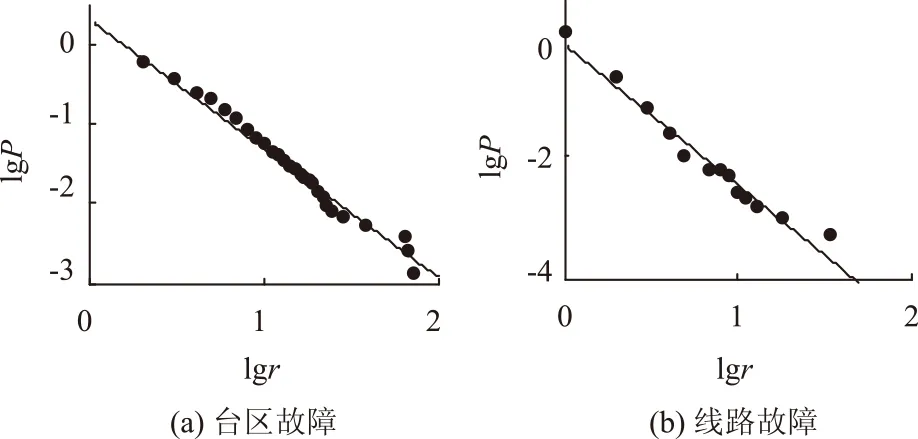
图5 双对数坐标下多空间尺度故障次数累积概率密度Fig.5 Multi-space cumulative probability density distributions of failure number on the double logarithmic coordinates

由图4、图5可得，在不同的时间和空间尺度下，配电网停电故障次数在双对数坐标下呈直线，近似服从幂律分布。从分形的特性来看，配电网故障次数具有自相似性。

3 形成机理分析

图6 A市配电网日故障时序图Fig.6 Time sequence diagram of daily fault in distributionnetwork of A city

文献[13]中提及输电网在冰灾期间故障率数倍于其他时间段使输电网故障的概率分布具有幂律特征，文献[5]通过对H省500kV输电线路故障的统计分析，得出在恶劣条件下短时间内的多次故障爆发使其具有幂律特征，而其中并没有包括冰灾等恶劣条件。文献[10]指出城市配网具有环岛效应使其受冰灾影响小，而暴雨等极端天气才是使其具有幂律分布特征的始因。本文在对H省停电事故进行统计分析时，故障原因为冰灾、雷雨的情况较少，且并不密集。由于幂律分布表现出明显的尖峰厚尾特性[5]，所以本文首先从最直观的角度出发将配网停电性质细分为主线故障和配变停电分析其直接原因。图6所示为配网总停电故障、线路跳闸和配变停电的时序图。

总的来说，配网总停电故障时序图呈现出尖峰厚尾特性。但其中线路跳闸时序图分布较均匀，而配变停电时序图依然呈现出尖峰厚尾的特性。因此，本文将总停电故障分为线路跳闸和配变停电两部分分开讨论其时空分布特性。配变停电和线路跳闸的拟合结果如图7所示。

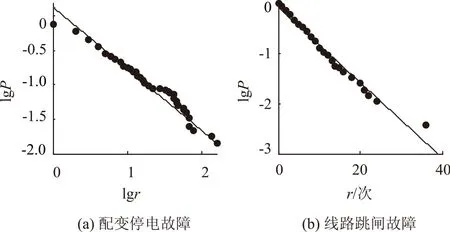
图7 单-双对数坐标下日故障次数对比分析图Fig.7 Comparative analysis of daily failure number on the single and double logarithmic coordinates

在图7中可以看出，配变停电的日故障次数在双对数坐标下呈直线状，而线路跳闸日故障次数在单对数坐标下呈直线状，服从指数分布。因此，导致A市配电网故障次数具有幂律特征的直接原因是配变停电。接下来从时间和空间上分别讨论配变停电在双对数坐标下呈直线的形成机理。

首先从时间角度来分析其形成机理。从图8中可见，在单对数坐标下配变停电拟合曲线尾部明显后翘，将使得曲线尾部后翘的故障多发日期提取出来，如表3所示。

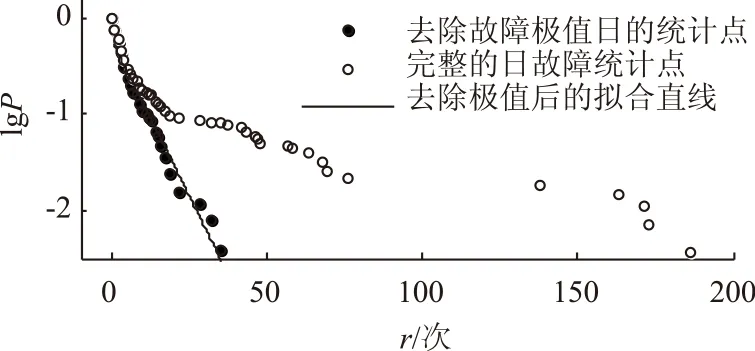
图8 单对数坐标下配变停电去除多发日前后累积概率分布Fig.8 Transformer outage cumulative probability distribution contrast on the single logarithmic coordinates before and after removal of the fault-prone days

从表中可以看出，配变停电次数最多的前3%故障多发日基本处在7月下旬至8月上旬，故障多发日故障次数占到了总停电次数的47.37%。

表3 A市前3%配变停电极值日Tab.3 The top 3% date of transformer outage in A city

同时，这1 259次故障中，由于过负荷、设备老化导致的配变故障占比达到了83.88%。究其原因主要由于夏季持续高温，用电负荷不断增加导致配电变压器容量超出限制，从而出现配变停电故障；设备老化等问题使设备容量达不到最初设计安装时的标准，这种情况在夏季负荷高峰期表现的尤为明显。

图8所示为配变停电故障在单对数坐标下去除前3%故障多发日的前后对比图。去除极值日后，配变停电在单对数坐标下呈直线，服从指数分布。

接下来从空间角度来分析其形成机理。将A、B、C、D这4个城市的配变停电以台区为单位进行统计，横坐标为台区的配变停电次数，纵坐标为台区配变停电次数的累积概率密度，在单对数坐标下进行拟合，可见拟合曲线尾部同样明显上翘，在此基础上去除停电次数较多的极值台区后，在同一个坐标下进行拟合，与未去除极值台区的对比图如图9所示。可以发现，去掉极值点后的台区配变停电次数在单对数坐标下呈直线，服从指数分布。

将A、B、C、D这4个城市故障停电次数较多的前0.5%的台区提取出来，统计结果见表4。

通过分析极值部分故障原因，发现人口较为密集、经济较发达的A、B、C这3个城市其极值部分故障原因多为过负荷、设备老化和运行不当等综合因素影响所致，且在夏季高温时期数日内多次发生故障情况较多；而经济较为落后的D市其极值部分故障原因为过负荷的情况较少，大多为雷雨天气导致。

本节从时间和空间两个角度分析配变停电幂律分布形成的物理本质，对配电网的安全稳定运行具有以下指导意义：年配变停电次数较多的台区由于设备老化等原因，尤其在夏季用电负荷高峰期间，对配电网供电可靠性的影响较大。因此，在迎峰度夏期间应注意生产及生活用电，及时发现超报装容量用电事件，避免超负荷情况发生；对于故障频发台区及时进行规划和技术改造，改善配网薄弱环节，从而提高配电网供电可靠性。

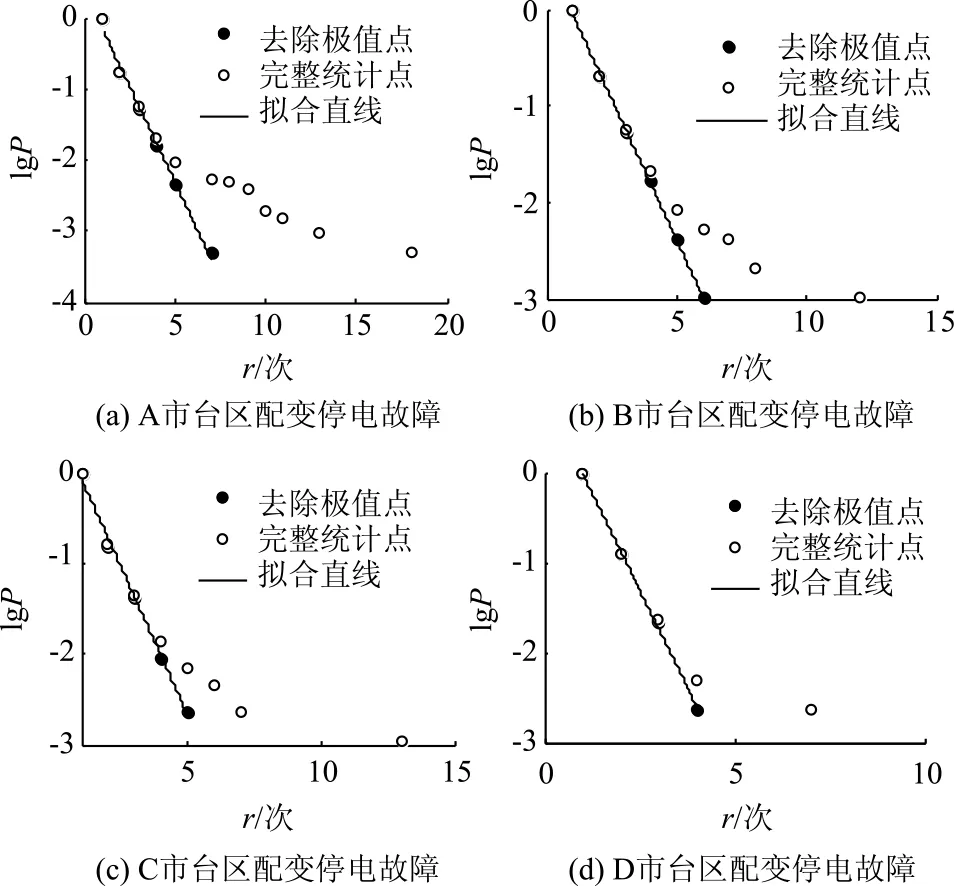
图9 单对数坐标下配变停电次数的累积概率密度分布Fig.9 Cumulative probability density of distribution transformer outage times in single logarithmic coordinates

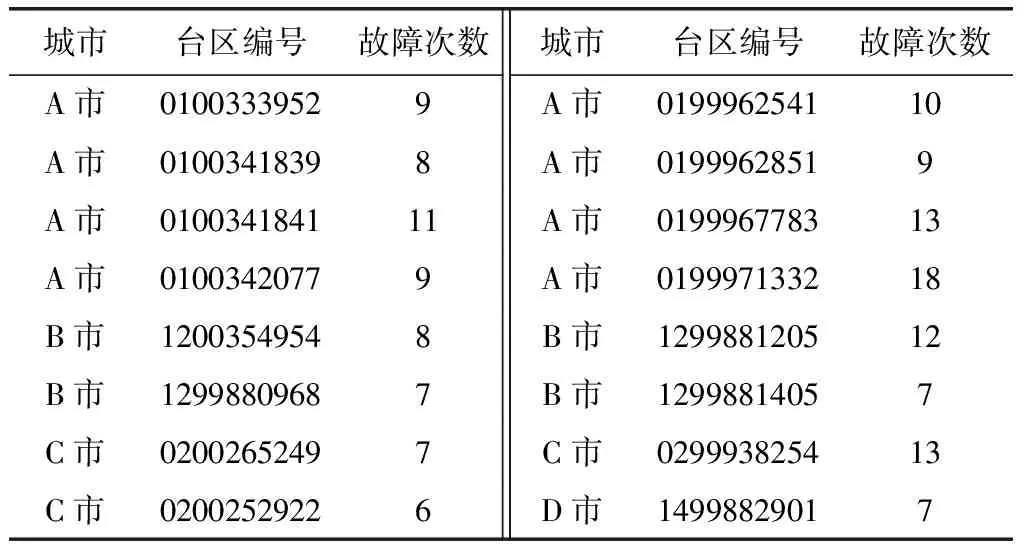
城市台区编号故障次数城市台区编号故障次数A市01003339529A市019996254110A市01003418398A市01999628519A市010034184111A市019996778313A市01003420779A市019997133218B市12003549548B市129988120512B市12998809687B市12998814057C市02002652497C市029993825413C市02002529226D市14998829017

4 各地市故障时空特性对比分析

为了探究各地市之间配变停电故障在时空上的演变过程是否具有相似性，将各地级市配变停电故障次数及其累积概率在同一双对数坐标下拟合进行对比分析。由于数据来源于配网抢修指挥平台，某些地级市由于平台投入时间短、覆盖度不够全面等原因，本文只分析数据完善的地级市。

首先从时间上对各地市进行对比分析。配变停电日故障次数及其累计概率的拟合结果如表5所示。从表5的数据可知，各地级市配变停电日故障次数拟合效果较好。同时，D、E两市，B、C、F、G这4个城市在双对数坐标下的拟合直线近似平行，如图10所示。

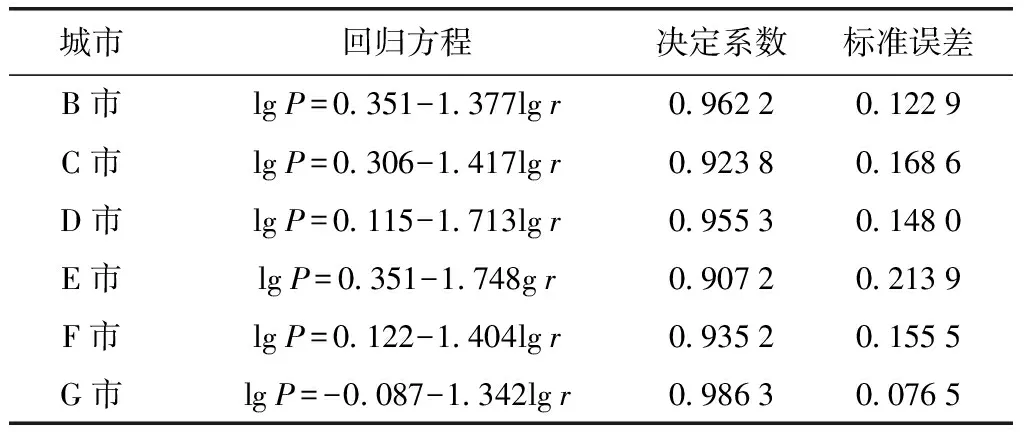
表5 不同地市日故障次数统计特性拟合直线Tab.5 The fitted functions of daily fault number statistics in different cities

图10 双对数坐标下不同地区日故障次数的概率分布图Fig.10 Daily fault number probability distribution contrast in different cities on the double logarithmic coordinates

从上节形成机理分析，由于各地市均隶属H省，各地市间纬度相近，天气温度也具有相似性，夏季负荷高峰期、故障多发日基本属于同一时期。因此，纬度接近、气候相近的各地级市在时间分布特征的形成过程中具有相似性。

类似的，从空间上对各地市进行对比分析。以台区为单位的配变停电台区年故障次数及其累计概率的拟合结果如表6、图11所示。

从空间分布特征的形成机理分析，以台区为单位的配变停电年故障次数和各配电变压器的投入运行时间、运行状况息息相关。由于各地级市台区配变投入运营时间不同，老化程度不同，因此各地级市故障特征在空间上的演变过程不具备相似性。

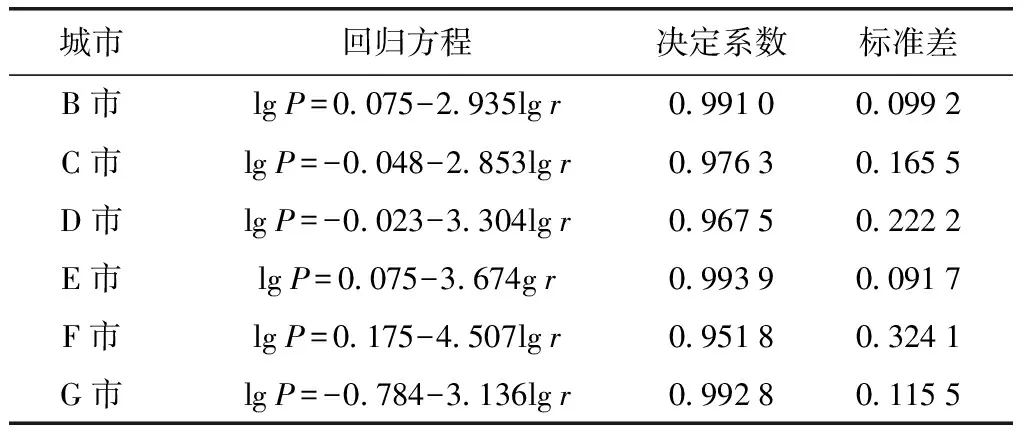
表6 不同地市故障空间统计特性拟合直线Tab.6 Fitted functions of transformer faults number statistics in different cities

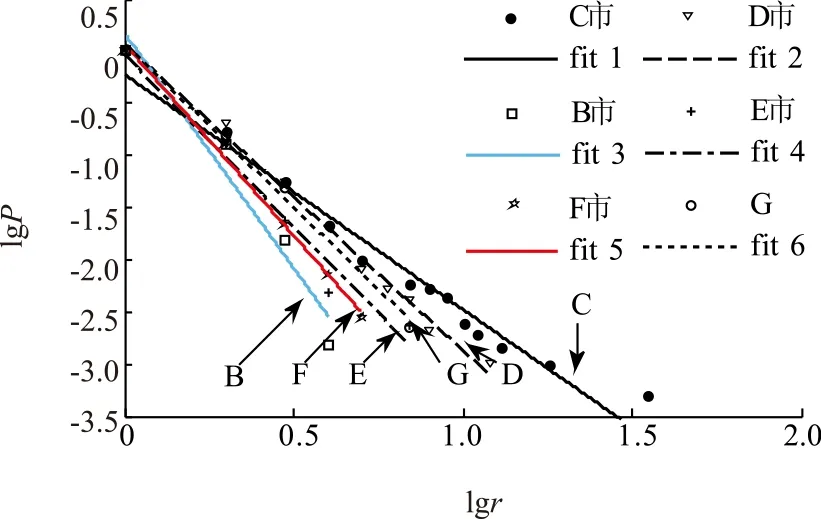
图11 双对数坐标下不同地市空间特征分布图Fig.11 Spatial characteristic diagram of different cities under double logarithmic coordinates

5 结 论

本文通过对2016—2017年期间H省各地市配网停电事件在多时间和多空间尺度进行对比统计分析，得出以下结论：

① H省各地市配网停电事件出现的频次及其累积概率在多时空的双对数坐标下呈直线，近似服从幂律分布，具有自相似性。

② 导致H省配电网故障次数具有幂律特征的直接原因是配变停电，根本原因是连续高温下的过负荷和设备老化等原因。针对各台区变压器之间发生故障的频次有明显的差异，某些台区在天气恶劣的条件下故障频发，某些台区从未发生过故障，可以通过数据分析找到配电网的薄弱环节，从而提出针对性的措施以提高配电网供电可靠性。

③ 通过对各地市时空分布特征在同一标度-频度下对比发现，由于地市间纬度、气候相近，各地市故障特征的演变在时间上具有相似性；在空间上由于地市间配变投入运行情况不同，其演变过程不具有相似性。