基于两阶段线性模型的微电网实时优化调度方法
陈卫东,梁 朔,肖园园,郭 敏
(广西电网有限责任公司电力科学研究院,广西南宁 530023)
0 引 言
近年来,随着化石能源的日益枯竭和人们环保意识的不断增强,以微型燃气轮机、光伏电池和风力发电为代表的分布式发电(distributed generation, DG)技术得到了广泛关注。微电网作为在此基础上发展起来的新技术,成为分布式发电综合利用的一种有效手段。它既能够充分发挥 DG 的作用,同时也能改善用户电能质量、提高供电可靠性,因而得到了广泛的应用[1]。
微电网系统惯性小,对负载功率波动承受能力差[2];离/并网运行方式的不同和储能单元的存在又增加了微电网内部能量传输路径和方向的多样性、复杂性[3]。因此,微电网安全经济的运行都必须以完善的能量优化调度系统为支撑,最终实现对各发电单元和储能单元的合理调度控制。微电网的能量调度从时间尺度上可以分为日前(短期)能量调度和实时(超短期)能量调度两大类[4-5]。微电网的日前能量调度是在日前预测的基础上制定未来一天各可控微电源的开停机计划和各发电单元的整点出力计划;而微电网实时能量调度则是在满足能量平衡和各电源出力限值约束的条件下制定各电源未来超短期出力计划[6]。所以微电网实时能量调度对微电网的安全高效运行发挥着至关重要的作用。
关于微电网实时能量调度,国内开展了很多研究工作。文献[7]建立了一种基于信息物理系统的微电网孤岛模式下有功功率实时调度模型,用一致性协同算法进行求解,但没有考虑微电网并网模式的调度问题。文献[8]提出了一种基于滑动平均滤波法对微电网实时波动功率在混合储能中合理分配的方法,但所提方法要求微电网需配置混合储能设备,对一般微电网不具有普遍适用性。文献[9]提出了一种采用改进粒子群算法的双层优化调度方法,解决微电网并网实时能量优化调度问题,但需要多次迭代计算才能取得理想解,计算耗时较长。文献[10]提出了将蓄电池充放电成本以罚函数形式计入目标函数的微电网实时能量调度模型,但缺乏与日前调度计划相结合对全天运行情况的整体调度,具有一定的局限性。文献[11]基于文献[12]提出的储能SOC日前调度计划,利用最小费用最大流网流方法将非线性约束条件线性化,加快了模型的求解速度,但处理过程比较复杂。
本文同样基于文献[12]提出的储能SOC日前调度计划,首先分析微电网实时状态空间下的调度策略,随后建立基于储能系统充放电引导系数的“等效供电成本最小”和实际供电成本最小的两阶段线性模型,最后通过微电网各实时状态下优化调度仿真和有/无储能SOC日前计划情况下的实时调度仿真实验验证模型和方法的有效性。
1 微电网实时优化调度策略分析
微电网实时调度是对下一个调度周期分布式电源出力的静态优化问题。本文根据微电网的负荷状态、储能单元的荷电状态、下一调度周期所处的运行时段,在并网和孤岛两种模式下对微电网运行状态空间进行划分,研究相应的实时调度策略。
为便于介绍实时调度策略,定义SOC0为当前时刻储能单元的荷电状态,SOCb为根据日前计划得到的下一个调度周期(5 min)的最佳荷电状态计划。
(1)
式中:SOCh、SOCh+1为根据储能SOC日前计划得到的储能单元每小时整点的最佳荷电状态。
1.1 微电网运行状态空间划分
为了便于描述微电网的运行状态,需要对微电网的不同运行状态进行划分,用状态空间向量表示微电网的运行状态。
定义1:等效净负荷(微电网负荷与可再生能源发电功率之差)状态变量E用来描述微电网当前可再生能源总发电功率与总负荷的供求关系。E的表达式为
(2)
式中:PNetLOAD,t为t时段等效净负荷的预测值。
(3)
式中:PLOAD,t为t时段总负荷预测值;M为不可控可再生能源电源总数;PUCi,t为第i台可再生能源电源t时段发电功率预测值;PLOSS,t为t时段微电网网损。
定义2:储能水平状态变量L用来描述微电网当前储能荷电状态SOC0与下一个5 min时段最佳荷电状态SOCb比较的关系,将表征下一调度周期储能应有的充/放电状态。L的表达式为
(4)
定义3:峰平谷状态变量T用来描述微电网下一调度周期所处的运行时段。设下一调度周期为t,则T的表达式为
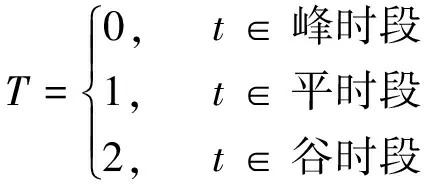
(5)
由上述3个状态变量构成的系统状态向量Z为
Z=[T,E,L]
(6)
根据各状态变量取值不同的组合,可以将微电网运行的状态空间划分为12种状态,如真值表1所示。
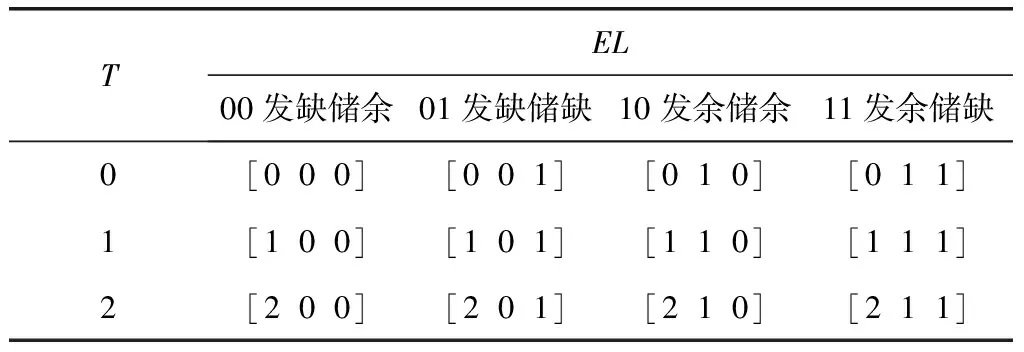
表1 微电网实时状态空间真值表
1.2 并网模式下实时调度策略分析
当微电网处于表1所示不同状态时调度模型应对电网交互功率和储能系统充放电采取不同的控制策略。在本文第一阶段“等效成本”最小建模中假定系统不足功率全部由电网“购入”,统称为“购电”功率,也就是不区分购电功率和可控微电源出力。
表1第1列和第2列所示系统状态为等效净负荷大于0的情况,也就是风光发电不足以满足微网内部负荷需求。具体调度控制策略如下:
策略A:第1列“发电不足储能有余”状态([000]、[100]、[200])控制策略是优先放电供给网内负载;若放电功率不足以满足负载则“购电”供载,若放电功率供载有余则在峰时段([000])时“放电售电”,在平和谷时段([101]、[201])不允许“放电售电”。
策略B:第2列“发电不足储能缺额”状态控制策略是首先“购电”供载;在平和谷时段([101]、[201])应“购电”对储能单元进行充电,在峰时段([001])则不允许进行“购电”充电。
表1第3列和第4列所示系统状态为等效净负荷小于0的情况,也就是风光发电满足微网内部负荷有余。具体调度控制策略如下:
策略C:第3列“发电有余储能有余”状态([010]、[110]、[210])控制策略是优先“发电售电”,若售电功率未达上限则“放电售电”;若售电功率已达上限,发电有余则“发电充电至最高储能SOC”,若发电仍余则“减少发电功率”。
策略D:第4列“发电有余储能缺额”状态控制策略是首先“余电充电”;若充电有余则在峰时段([011])“余电售电”,在平和谷时段([111]、[211])“继续充电直至最高储能SOC”仍有余则“余电售电”;若充电不足在平和谷时段([111]、[211])则““购电”充电”,峰时段([011])则不允许“购电”充电。
1.3 孤岛模式下实时调度策略分析
孤岛运行模式下,微电网内负荷需求完全由系统内微电源和储能装置来满足。状态向量第一个元素没有意义。系统状态空间由4种状态组成:
{[×00], [×01], [×10],[×11]}
注意在孤岛情况下,供电策略分析时所谓“购电”仅限于网内可调度微电源出力,4种状态下的控制策略如下:
策略E:孤岛“发电不足储能有余”([×00])状态控制策略是“优先放电供给负载;若放电功率不足以满足负载则‘购电’供载”。
策略F:孤岛“发电不足储能缺额”([×01])状态控制策略是“优先‘购电’供载”;若“购电”功率未达上限,则“购电充电”;若“购电”功率不足以满足负荷需求,则“按类别减载”。
策略G:孤岛“发电有余”([×10],[×11])状态控制策略是“余电充电直至上限”,若仍有余则“减发电功率”。
2 微电网实时优化调度两阶段线性模型
微电网实时优化调度要求寻优过程快速、收敛可靠。为此,本文将实时优化问题分两阶段进行优化,分别建立基于储能系统充放电引导系数的“等效供电成本最小”的线性模型和基于实际供电成本最小的线性模型。在第一阶段模型中,将可再生能源小于电网负荷的不足功率统称为“购电”功率,不区分是来源于从电网购电还是依靠可调度型微电源供电;第二阶段模型以实际供电成本最小为目标,确定可调度型微电源出力和电网买入功率之间的最佳分配方案。
2.1 “等效供电成本最小”实时优化调度模型
模型中“等效成本”包括:储能系统充放电等效成本、“购电”功率等效成本和实际售电成本。储能系统充放电成本称之为等效成本是因为,在线性规划模型中,欲调节储能设备与其他电源的出力,需将储能设备的充放电引导系数作为成本系数出现在目标函数中,参与和其它电源出力的竞争。“购电”功率成本系数称之为等效成本系数是因为,其一是“购电”功率包括电网购电功率和可调度型微电源的输出功率,二者成本不同;其二是其值的大小作为充放电等效成本系数的相对值以权衡与储能单元的出力系数。向电网售电成本采用实际运行时段的售电电价作为成本系数,为两个等效成本系数提供一个实际的标尺。
第一阶段优化决策问题可以描述为:在满足各变量输出限值约束和全网功率平衡约束的前提下,求微电网在下个实时调度周期的储能单元充放电功率、售电功率、“购电”功率的最佳控制方案,使等效供电成本最小。
该问题的控制变量为
K=[PBAT,PGRsell,t,Pbuy,t,PUC,t]
(7)
式中:t为实时调度周期(本文取5min);PBAT为储能单元的充放电功率,为正表示放电,为负表示充电;PGRsell,t为向电网售电功率;Pbuy,t为“购电”功率;PUC,t为可再生能源电源总的发电功率。
2.1.1 目标函数
minCEQ=cbuy,tPbuy,t+cBAT,tPBAT-SGRcGRsell,tPGRsell,t
(8)
式中:cbuy,t为下一调度周期的等效“购电”成本系数;cBAT,t为储能单元“充放电引导系数”;SGR表示微网的运行方式,孤岛运行为0,并网运行为1;cGRsell,t为下一调度周期的实际售电电价。
2.1.2 约束条件
①功率平衡约束
Pbuy,t-SGRPGRsell,t+PBAT=PLOAD,t-PUC,t
(9)
式中:PLOAD,t为下一调度周期负荷的预测值。
②“购电”和售电功率约束
0≤PGRsell,t≤PGRsellmax,t
0≤Pbuy,t≤Pbuymax,t
(10)
式中:PGRsellmax,t和Pbuymax,t分别为下一调度周期微电网向上级电网售电功率上限和“购电”功率上限。“购电”上限值在并网模式下取电网购电和可调度型微电源输出总功率之和,孤岛模式下取后者。微电网向上级电网购电和售电功率为互斥约束,即:
PGRsell,tPbuy,t=0
(11)
虽然对于这两个控制变量的互斥约束是非线性的,但是这类问题在数学上通常可以用简单枚举加线性规划求解方法解决,所以可以认为是准线性规划问题。
③ 储能单元充放电功率约束
-PminBT(ΔSOCmin,t)≤PBAT≤PmaxBT(ΔSOCmax,t)
(12)
式中:PminBT(ΔSOCmin,t)和PmaxBT(ΔSOCmax,t)分别为由ΔSOCt上下限确定的放电和充电功率最大限值。
④可再生能源功率输出约束
0≤PUC,t≤PmaxUC,t
(13)
式中:PmaxUC,t为下一调度周期可再生能源预测总的输出功率。
2.2 充放电引导系数模型
在优化调度模型式(8)的目标函数中有3项成本系数,其中只有售电成本系数为给定该时段的售电电价,该项总金额为盈利以负号计入成本。另外两个系数均称为等效成本系数,是因为需要对表1给定的状态空间中所有状态确定这两个系数的相对大小以及相对售电成本系数的大小才能实现预期的调度策略,它们并没有实际价格意义。其中储能系统充放电等效成本系数即为充放电引导系数。
2.2.1 并网模式下充放电引导系数模型
目标函数的3个成本系数中,等效购电成本系数cbuy,t大于售电电价cGRsell,t的关系总是成立的,下面主要讨论cBAT,t与它们的相对关系。
首先讨论“发电不足”的状态,即在表1第1列和第2列所示系统状态为等效净负荷大于0的情况,也就是风光发电不足以满足微网内部负荷需求状态。
当电网处于第1列“发电不足储能有余”状态时,采用策略A。此时发电不足储能有余,因此由储能放电和“购电”共同承担剩余负荷,由购电与售电互斥约束,售电功率为0。此时应该优先放电,所以充放电引导系数应小于购电成本系数。也就是,当SOC0≥SOCb时,cBAT,t取小于cbuy,t的数值。
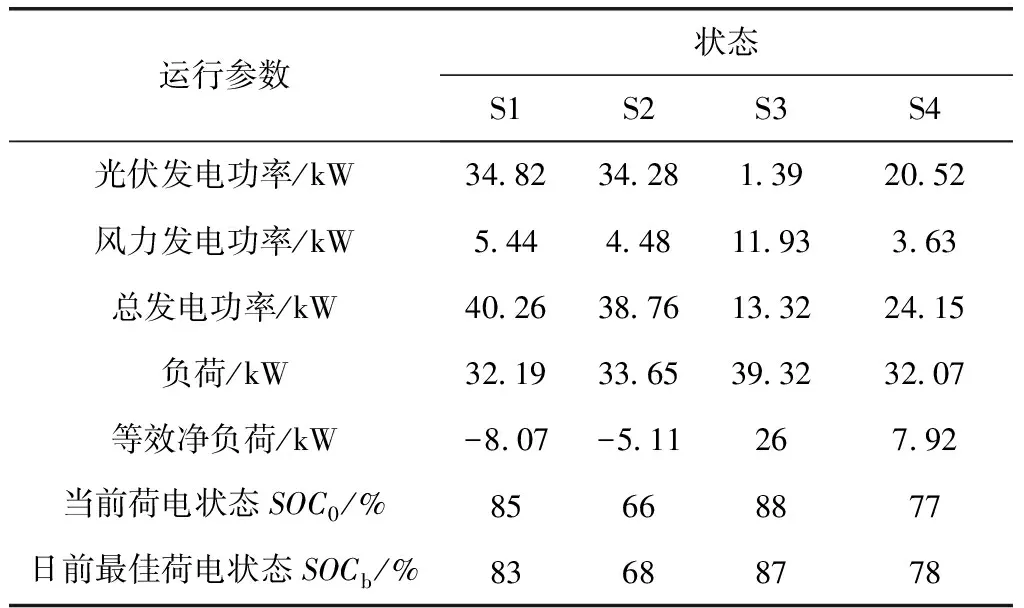
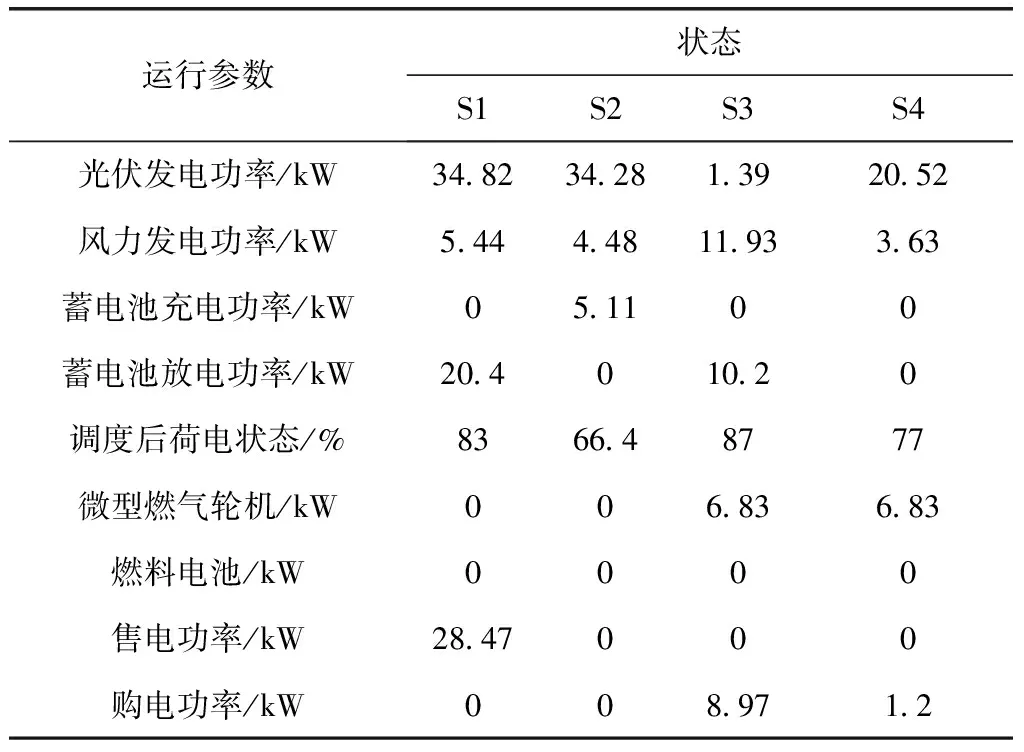
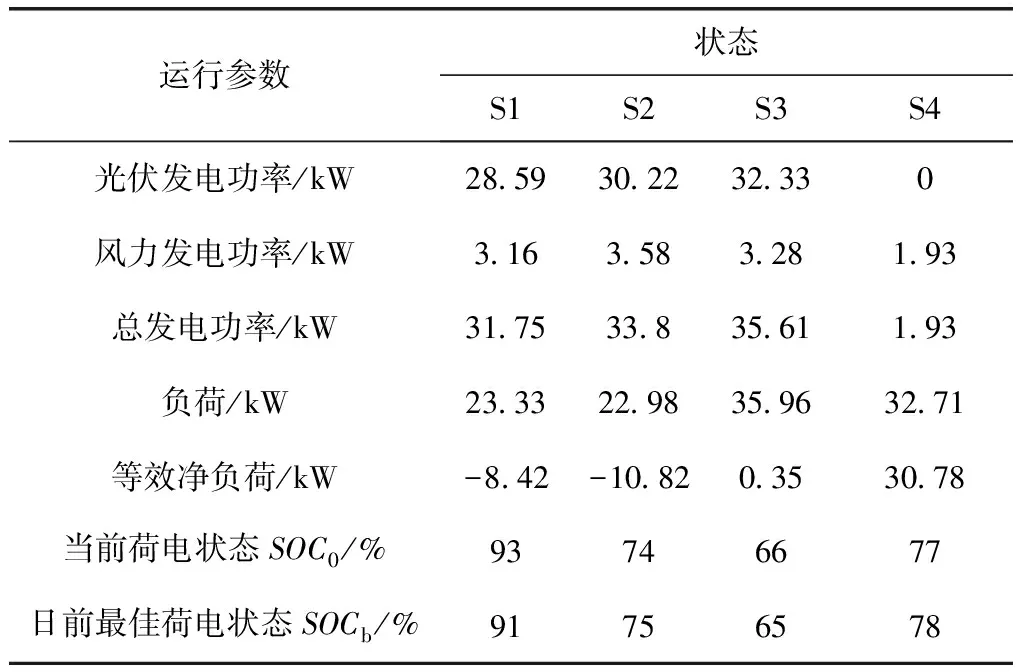
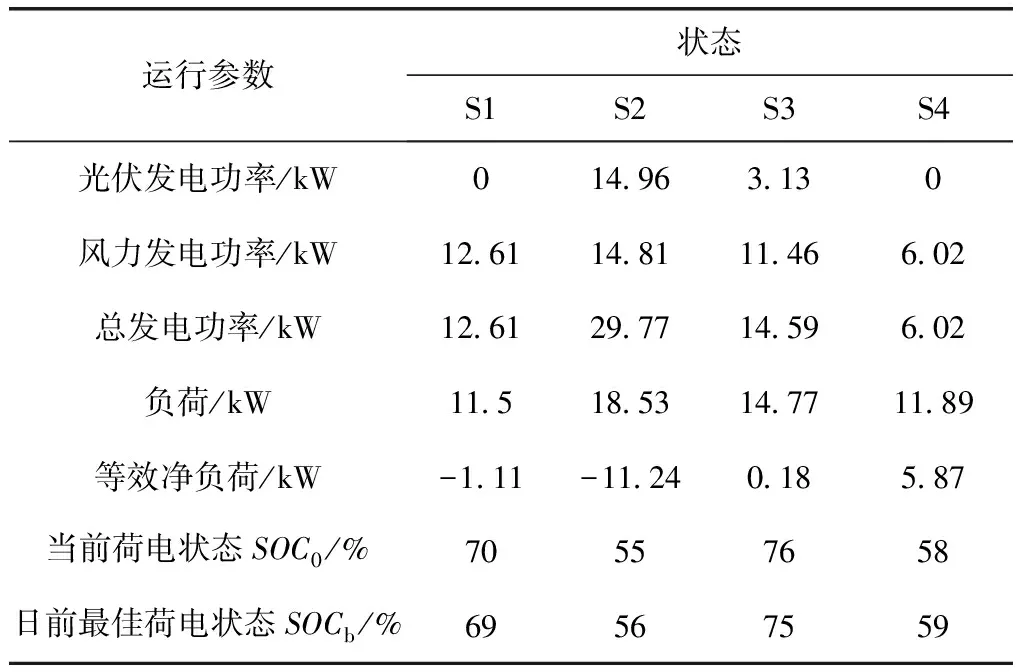
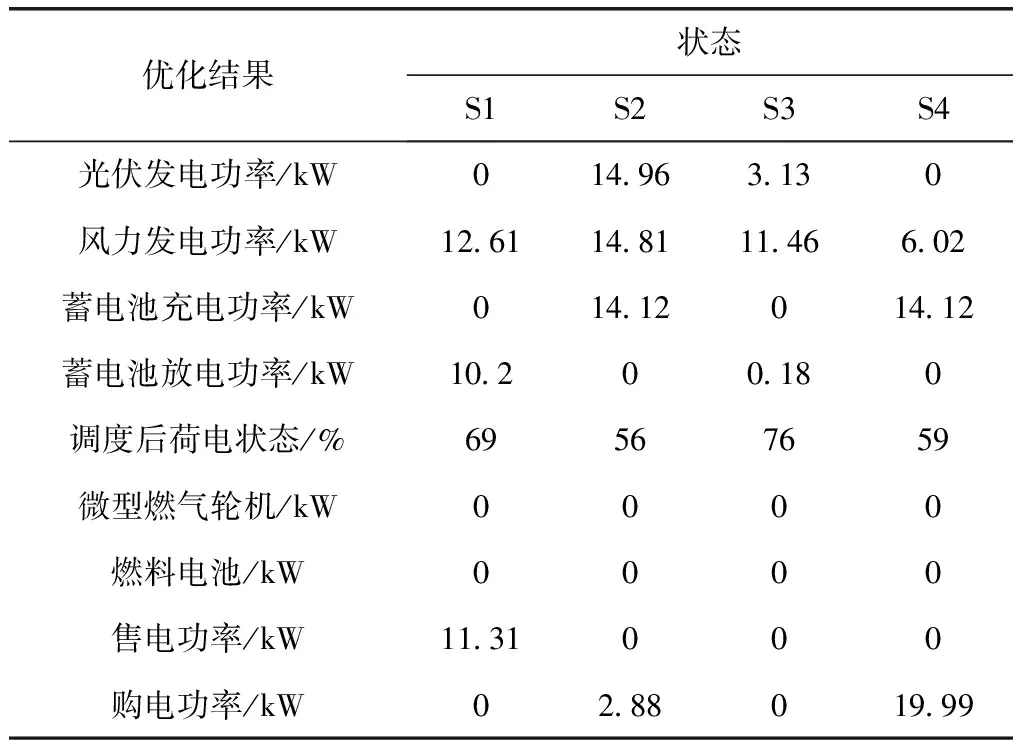
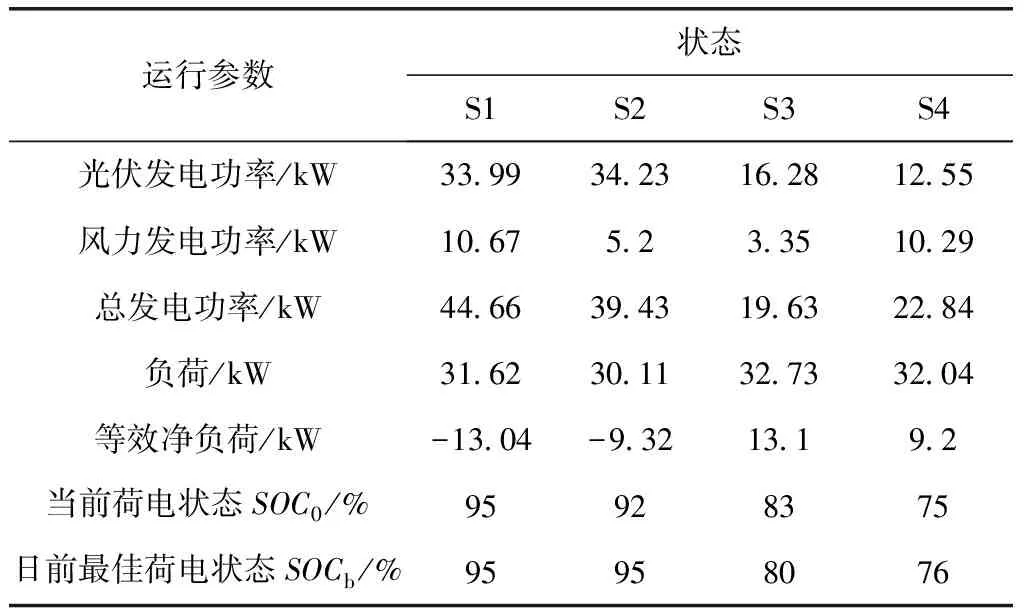
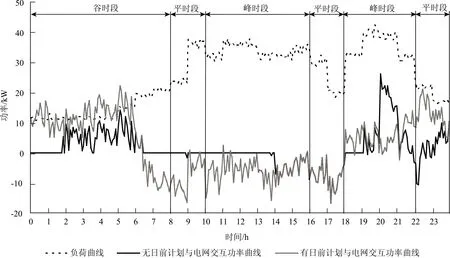
当电网处于第2列“发电不足储能缺额”状态时,采用策略B。优先“‘购电’供载”,所以充放电引导系数应大于购电成本系数。也就是,当SOC0 所以在“发电不足”的状态下,应建立的充放电引导系数和等效购电成本系数关系的经验公式为 (14) minCEQ=cbuy,tPbuy,t+cBAT,tPBAT (15) 下面讨论“发电有余”的状态,即在表1第3列和第4列所示系统状态为等效净负荷小于0的情况。此时,主要是在储能单元充放电与向电网售电之间进行权衡。 当电网处于第3列“发电有余储能有余”状态时,采用策略C“余电售电优先”。此时,功率平衡约束中售电功率成了唯一的“漏”,所以必须大于0,由互斥约束“购电”为0。此时,应满足充放电引导系数小于售电电价。也就是,当SOC0≥SOCb时,cBAT,t取小于cGRsell,t的数值。 当电网处于第4列“发电有余储能缺额”状态时,采用策略D “余电充电优先”,所以充放电引导系数应大于售电成本系数。也就是,当SOC0 所以在“发电有余”的状态下,本文建立的充放电引导系数和等效购电成本系数的经验公式为 (16) (17) 2.2.2 孤岛模式下充放电引导系数模型 首先讨论“发电不足”的状态,即[×00] [×01],也就是风光发电不足以满足微网内部负荷需求的状态。 当微电网处于“发电不足储能有余”状态时,采用策略E。此时发电不足储能有余,因此由储能放电和“购电”共同承担剩余负荷。此时应该放电优先,所以应满足充放电引导系数小于“购电”成本系数的关系。也就是,当SOC0≥SOCb时,cBAT,t取小于cbuy,t的数值。 当微电网处于“发电不足储能缺额”状态时,采用策略F。优先“‘购电’供载”,所以充放电引导系数应大于“购电”成本系数。也就是,当SOC0 所以在“发电不足”的状态下,本文建立的充放电引导系数的经验公式为 (18) 此时: minCEQ=cbuy,tPbuy,t+cBAT,tPBAT (19) 下面讨论“发电有余”的状态,即[×10],[×11]。 当电网处于“发电有余”状态时,采用策略G“余电充直至上限”。此时,功率平衡约束中的“漏源”只有储能单元,所以其不能放电,且无需开启可调度电源。也就是,cBAT,t取恒小于cGRbuy,t的数值。 所以在“发电有余”的状态下,本文建立的充放电引导系数的经验公式为 cBAT,t=βcbuy,t (20) 式中:0<β<1。此时: minCEQ=cBAT,tPBAT(ΔSOCt) (21) 该决策问题的控制变量为:下一调度周期从电网购电功率和各可调度型微电源的发电功率。 2.3.1 目标函数 (22) 式中:Cfact表示下一调度时段的实际供电成本;ci为第i个可调度型微电源的发电成本;cGRbuy,t为下一调度周期的实际购电价格;Pi,t为下一调度周期第i个可调度型微电源的输出功率;Si,t为由日前计划制定的下一调度周期第i个可调度型微电源的运行/停运状态,1表示运行状态,0表示停运状态;N为微电网中可调度型微电源总数。 2.3.2 约束条件 ①“购电”功率和约束 下一调度周期电网与可调度型微电源功率输出的和必须满足第一步“等效供电成本”优化出的“购电”功率,即 (23) ②可调度型微电源输出功率约束 下一调度周期可调度型微电源的输出功率由微电源的出力变化范围和输出容量共同决定,功率输出上限取二者中较小值,下限取两者中较大值,即 max{PCmin,i,Pi,0-rdiΔt}≤Pi,t≤ min{PCmax,i,Pi,0+ruiΔt} (24) 式中:PCmin,i、PCmax,i分别为第i个可调度型微电源允许的最小输出功率和最大输出功率;Pi,0为第i个可调度型微电源的当前输出功率;rdi、rui分别为第i个可调度型微电源的最大减出力变化率和最大增出力变化率;Δt为5min。 ③ 微电网从电网购电功率约束 0≤PGRbuy,t≤PGRbuy max (25) 式中:PGRbuymax为微电网从电网实际购电的最大功率。 以并网方式为例,所提方法从状态判断到相应模型求解的整体流程如图1所示。 图1 优化求解流程图Fig.1 Optimization solution flow chart 主要求解步骤如下: ①由日前计划储能单元最佳荷电状态和实时运行参数,计算当前运行状态向量Z。 ②根据等效净负荷E、储能水平L判断当前运行状态所属状态空间。 ③依据所属状态空间执行相应的实时调度策略,求得下一调度周期对应策略下储能单元充放电引导系数cBAT,t和“购电”成本系数cbuy,t。 ④运用线性规划方法——单纯形法[13]求解“等效供电成本最小”模型,求得“购电”功率、售电功率和储能单元充放电功率。 ⑤再次运用单纯形法求解实际供电成本最小线性模型,求得电网交互功率和各可调度型微电源输出功率。 本文以文献[12]提供的微电网数据为例,设计系统在并网模式及孤岛模式中状态空间各状态下的仿真实验,验证按所提出的实时优化模型计算所得的计划方案符合实时调度策略。系统中包含风力发电单元(60kW)、光伏发电单元(80kW)、微型燃气轮机(30kW)各1台,还配置有一组蓄电池(200Ah)作为储能单元。系统详细的运行参数、各发电单元的额定参数和电网不同时段的购售电价格,见文献[12]。 4.2.1 各模式下调度实验 ①并网模式下峰时段 系统运行在峰时段时,列举4种状态,分别为:S1.调度时刻等效净负荷小于零,储能单元当前荷电状态高于日前计划给出的最佳荷电状态,即Z=[0 1 0];S2.调度时刻等效净负荷小于零,储能单元当前荷电状态低于日前计划给出的最佳荷电状态,即Z=[0 1 1];S3.调度时刻等效净负荷大于零,储能单元当前荷电状态高于日前计划给出的最佳荷电状态,即Z=[0 0 0];S4.调度时刻等效净负荷大于零,储能单元当前荷电状态低于日前计划给出的最佳荷电状态,即Z=[0 0 1]。系统具体运行数据见表2,按实时优化调度模型进行计算,运算结果如表3。 表2 系统峰时段运行数据 优化结果表明:在峰时段,当等效净负荷小于零时,可调度电源不发电,余电优先满足储能单元 表3 峰时段实时优化调度结果 的日前计划需求。当等效净负荷大于零时,可调度电源选择性出力,若储能单元荷电状态高于最佳荷电计划则放电;低于日前计划不再充电。优化结果符合峰时段实时调度策略。 ②并网模式下平时段 系统运行在平时段时,同样列举4种状态,其简述与峰时段类似,在此不再赘述。系统具体运行数据见表4,按实时优化调度模型进行计算,运算结果如表5。 表4 系统平时段运行数据 优化结果表明:在平时段,可调度电源不发电,当等效净负荷小于零时,余电优先满足储能单元的日前计划需求;当等效净负荷大于零时,若储能单元荷电状态高于最佳荷电计划则放电供载;低于最佳荷电计划则购电充电。优化结果符合平时段实时调度策略。 表5 平时段实时优化调度结果 ③并网模式下谷时段 系统运行在谷时段时,列举同样4种状态。系统具体运行数据见表6,按实时优化调度模型进行计算,运算结果如表7。 表6 系统谷时段运行数据 优化结果表明:在谷时段,可调度电源不发电,当等效净负荷小于零时,余电优先满足储能单元的日前计划需求。当等效净负荷大于零时, 若储能单元荷电状态高于最佳荷电计划则放电供载;低于最佳荷电计划则购电充电。优化结果符合谷时段实时调度策略。 ④ 孤岛模式 表7 谷时段实时优化调度结果 系统运行在孤岛状态时,列举4种状态分别为:S1.该时刻等效净负荷小于零,储能单元当前荷电状态等于最高荷电状态;S2.该时刻等效净负荷小于零,储能单元当前荷电状态低于最高荷电状态;S3.该时刻等效净负荷大于零,储能单元当前荷电状态高于计划给出的最佳荷电状态;S4.该时刻等效净负荷大于零,储能单元当前荷电状态低于计划给出的最佳荷电状态。系统具体运行数据见表8,按实时优化调度模型进行计算,运算结果如表9。 表8 系统孤岛运行数据 优化结果表明:系统孤岛运行时,若等效净负荷小于零,则多余电能给储能单元充电,如果充到上限仍有余,则减少可再生能源出力(本文设定优先减少光伏出力)。若等效净负荷大于零,储能单元当前荷电状态高于最佳荷电状态,则放电,不足部分由可调度电源补充;若低于最佳荷电状态,则由可调度电源发电供载,有余力的情况下给储能单元充电。优化结果符合系统孤岛模式下的实时调度策略。 表9 孤岛运行优化调度结果 4.2.2 有/无储能(SOC)日前计划下的实时调度比较实验 以文献[12]提供的案例数据为基础,利用本文创建的模型和算法对微电网有无储能(SOC)日前计划进行实时调度比较,得到某一天微电网与电网的功率交互曲线,如图2所示。由图可知,遵循储能(SOC)日前计划的实时调度曲线能够全天参与电网的削峰填谷,而缺乏储能(SOC)日前计划的实时调度曲线由于价格竞争的关系虽然也具有削峰填谷的作用,但只能部分时段参与而不能全过程参与。由表10可以看出,有日前计划调度全天总成本还不到无日前调度总成本的一半,经济效益十分明显。 图2 有无日前计划下微电网与大电网实时调度交互功率曲线Fig.2 The microgrid and large grid real-time scheduling interaction power curve with or without day-ahead plan ① 本文提出了基于储能充放电引导系数的“等效供电成本”和实际供电成本最小的微电网实时优化调度两阶段线性模型。第一阶段模型将向电网购电功率和可调度型微电源输出功率统一处理为“购电”功率,以“等效供电成本”最小为目标确定储能单元的充放电功率和购电功率;为此,基于实时调度状态空间各状态下应采取的控制策略,建立了储能系统充放电引导系数模型。第二阶段模型以实际供电成本最小为目标,确定不足功率在电网买入功率和可调度型微电源出力之间权衡的最佳决策方案。 ② 由仿真算例表明,利用所提出的遵循储能SOC日前计划优化模型能够严格执行各种状态下实时调度策略,同时能够从全天角度,进行储能单元和可调度型微电源的出力规划,可以获得十分突出的经济效益,且具有明显的削峰填谷的作用。
2.3 实际供电成本最小实时优化调度模型
3 求解流程
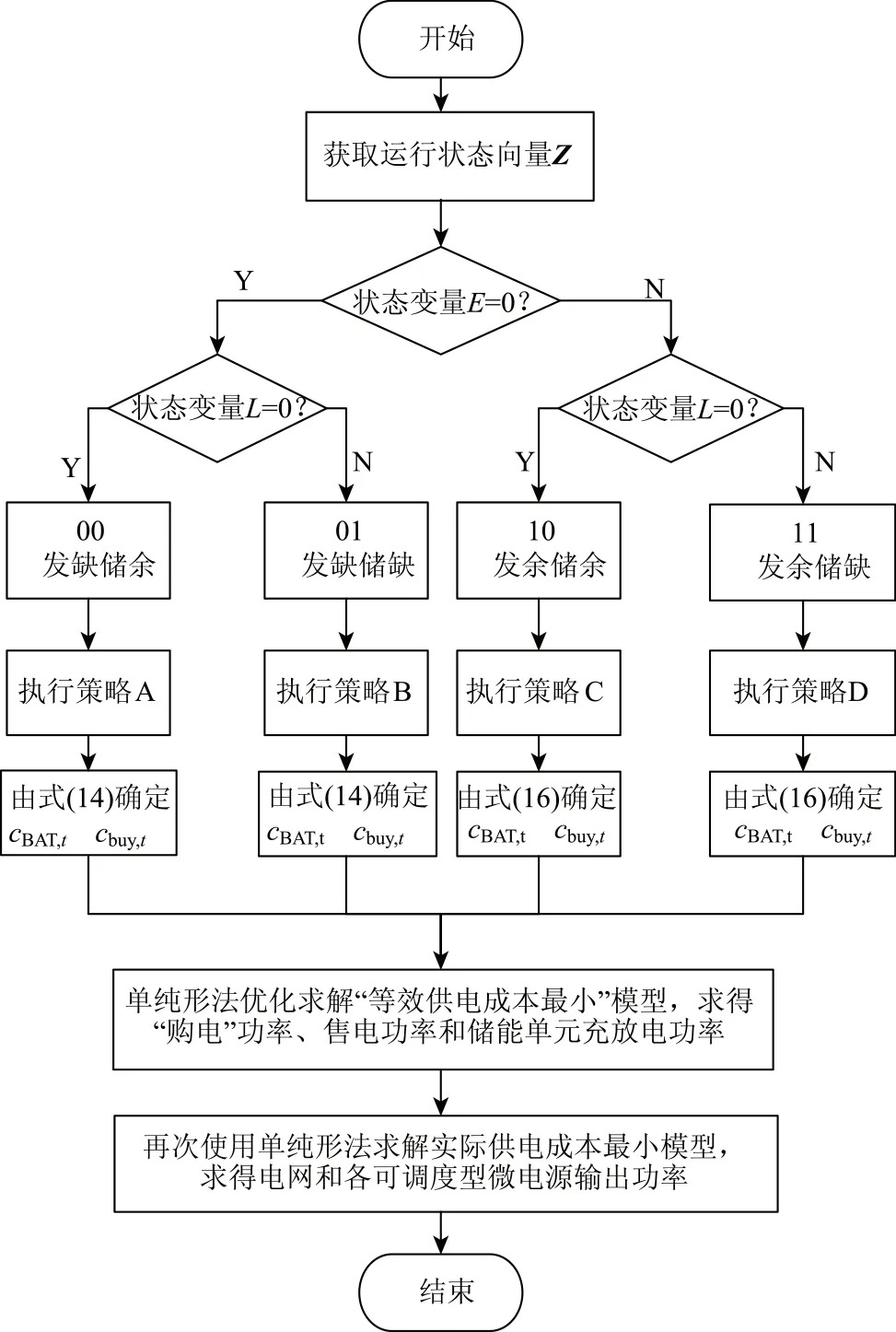
4 算例分析
4.1 基础数据
4.2 实验结果与分析


5 结 论

