风电场出力随机扰动下的电网概率脆弱性评估

赵任光，刘群英，陈树恒，张昌华，高旭光，陈明华

(电子科技大学，四川成都 611731)

0 引 言

电网脆弱性是指电网在正常运行情况下，局部在遭受扰动或者故障因素影响时，系统中局部或全部母线维持正常输电能力逐渐弱化的特性[1]。在实际电力系统运行中，发电机具有故障停运的随机性，负荷预测由于负荷功率的波动而存在偏差，再加上风电场等可再生能源发电的接入使得电力系统经受更多的随机性[2-3]，运行变得更加复杂多变，电网脆弱性研究也因此从确定性评估逐渐发展到随机性评估阶段。根据现有分析方法，电网脆弱性主要从电网状态和结构这两种机理进行脆弱性研究，评估电网状态脆弱性可以通过能量函数法[4]、短路容量[5]、灵敏度技术[6]等方法，来对系统中的脆弱节点和脆弱支路进行辨识。对于电网结构脆弱性，可以从复杂网络理论中带权重的电气介数和线路模型[7]、四层集合模型[8]以及加权潮流熵[9]，来识别系统在结构上的脆弱环节。

文献[10]利用犹豫模糊决策方法综合系统潮流分布和电网拓扑特性等因素，通过最小奇值定量分析和改进潮流熵来研究电网脆弱性。文献[11]通过改进DEAHP模型，从不同评估角度，利用主观偏好与客观数据的共同作用下来构建多层次多角度的脆弱性辨识体系。文献[12]结合含风电电力系统灵敏度分析法和熵权法，建立脆弱性评估模型。文献[13]基于支路势能函数模型，计算各支路当前输送值与初始值的偏离程度，来确定系统的脆弱区。

以上研究，在辨识脆弱环节上开辟了多种方法和多种角度，但都常规地研究状态和结构脆弱性机理，单一地对系统状态、拓扑结构、系统参数等其中部分因素来考察电网脆弱性势必存在不足，尤其在风电大规模并网的新时期电力系统中，因为风电的随机性导致了更加复杂的脆弱特性，这是脆弱性评估方法的探索面临的新挑战。基于概率的分析方法考虑多种内部和外部不确定因素，更能适应风电并网运行中的各种扰动并存的复杂情况，有利于发现电网中最不稳定、最脆弱的环节。

本文基于概率潮流的观点，综合考虑电力系统的多种随机不确定性因素的影响，基于以半不变量为基础的Gram-Charlier级数展开方法(CGC)来计算系统中的各节点电压和各支路功率传输的概率分布情况，并在此基础上结合节点临界电压和支路极限传输功率，提出了电网概率脆弱性的评判指标，辨识电网中的最脆弱环节，通过在含风电模型的IEEE-30母线系统中进行仿真分析，证明了所提的研究方法评估电网概率脆弱性的可行性和有效性，可为电网脆弱性的评估研究及系统的安全运行维护提供极为重要的借鉴作用。

1 基于Weibull分布的风电场概率模型

1.1 风电场风速的概率分布模型

为了在含风电电力系统中更好地拟合风速随机波动情况，通常采用Weibull(三参数)概率模型，该模型经过大量实际数据验证，能很好地符合90%以上地区的风速平均分布[14]。其风速概率密度函数为

(1)

式中:v为实际风速；k、c和v0为Weibull分布的3个参数，其中k表示形状参数，c表示尺度参数，v0表示位置参数。与式(1)等价的风速概率分布函数为

(2)

1.2 风电机组功率概率分布模型

风电机组的有功出力直接受到随风速变化的控制，其特性可归纳为式(3)所示。

(3)

式中:Pr为风电机组的额定有功出力；vw为实际风速；vr为额定风速；vin为切入风速；vout为切出风速；k1=Pr/(vr-vin)；k2=-k1vin。

根据风电系统实际运行特性可知，风电机组的有功出力与风速呈线性关系，且实际风速分布于切入风速和额定风速范围内。由式(1)、式(2)和式(3)可推导出风电机组有功功率的概率分布为

(4)

则风力发电机组有功功率的概率密度函数为

(5)

本研究所涉及的风力发电系统使用的是异步发电机，在正常运行过程中会吸收系统大量无功功率。为了精简系统复杂度且保持一定的准确性，通常假设在风电接入的电力系统中的电容器自动投切，使得风力发电机组易于分析，并将其设为功率因数恒定不变的PQ节点[14]。则无功功率概率分布可推导为

(6)

式中:φ为功率因数角，一般位于第四象限，所以tgφ为负值。

2 基于CGC方法的含风电电力系统运行状态的概率脆弱性分析

2.1 基于CGC方法的概率分布计算原理

概率潮流通过综合考虑风电并网的电力系统的系统参数、拓扑结构、节点负荷注入、支路输送能力、风力机和发电机出力等随机变化情况，来反映系统运行受各种随机扰动和故障的影响[14]。以基于半不变量和Gram-Charlier级数结合(CGC)方法来进行概率分析，显著地提高了随机变量的卷积运算效率，且精度满足要求。本文正是基于此原理，首次将CGC方法来分析风电并网系统脆弱性，弥补了单独考察节点或支路的脆弱程度，而忽视整体连接效应的不足。

Gram-Charlier级数通过正态随机变量各阶导数组成的级数来表达随机变量的分布函数，即

f(z)=φ(z)+c1φ(1)(z)+c2φ(2)(z)+…

(7)

式中：Gram-Charlier级数各项系数ci(i=1,2,3，…)可由半不变量来确定；f(z)为z的概率密度函数。

(8)

(9)

式中:Hγ(z)为Hermite多项式。由式(7)、式(8)和式(9)可得随机变量分布函数的Gram-Charlier级数展开式：

(10)

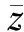
2.2 系统节点的临界电压和支路极限传输功率获取

将含风电电力系统进行戴维南等值，等值后的结构如图1所示的两机两母线系统，除风电系统外的其他电源统一等值为电压源串联等效阻抗的形式。

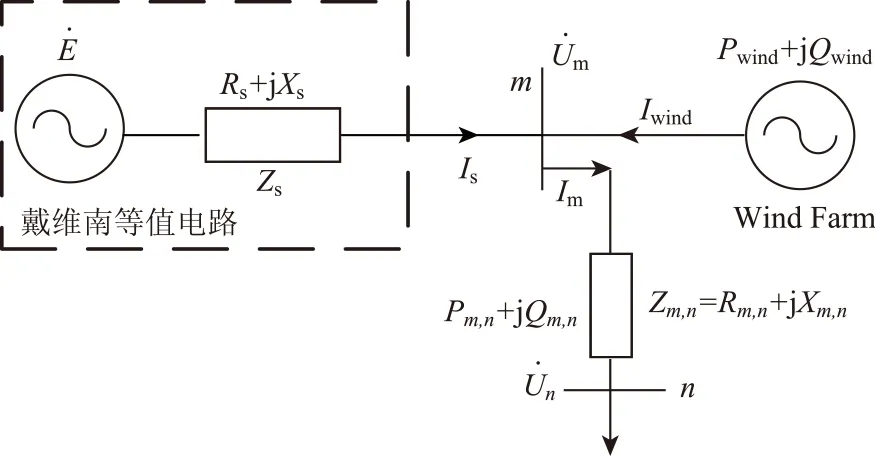
图1 接入风电场的电网戴维南等值系统Fig.1 The venin equivalent system of the load node access to wind farm

(Um,ncosθ+jUm,nsinθ)·

(11)

系统逼近电压崩溃的临界电压值：

(12)

当不接入风电场时，令Pwind=0和Qwind=0。已有文献证明在支路传输功率的功率因数不变情况下，该等效支路的极限传输视在功率为

(13)

式中:ZL∠φ=ZS+Zm,nZL，Zm,n为节点m和n之间的阻抗；cosφ为节点m和n之间的实际传输功率的功率因数，支路极限传输视在功率值Scr与支路传输功率的功率因数角φ有关。由于实际风电是随机变化的，所以对应的实际传输功率极限值也是不定的。以φ=φ时的支路传输功率值为理论极限传输功率值，并以此功率因数角φ分别求出极限传输有功功率Pcr和极限传输无功功率Qcr：

(14)

2.3 基于CGC方法的支路概率脆弱性评估

在风电并网的电力系统运行过程中，风电功率的波动往往造成其余节点注入功率的随机波动，高于或低于约束值时，会造成系统的不稳定状态，进而造成系统的脆弱化。考虑到节点注入功率由传统发电机注入功率随机变量ΔWG，负荷功率随机变量ΔWL和风力发电机注入功率ΔWwind构成，即ΔW=ΔWG+ΔWL+ΔWwind，假设注入各节点的功率随机变量具有独立性，则根据半不变量的可加性和线性关系可求出节点注入功率的各阶半不变量ΔW(k)，即

(15)

由式(15)可求出支路注入功率的各阶半不变量ΔZ(k)，即

(16)

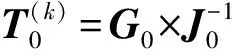
由此，可得到系统实际运行中支路传输有功功率和无功功率极限边缘取值，结合系统的临界支路极限传输功率值Pcr和Qcr，分别从支路有功和无功角度提出概率脆弱性评估指标CBP和CBQ：

(17)

(18)

式中:m,n表示节点m和n之间的支路；Pm,n，max和Pm,n，min为支路m,n运行时有功传输量Pm,n的最大值和最小值；Qm,n,max和Qm,n,min为支路m,n运行时无功吸收量Qm,n的最大值和最小值；Pcr,m,n和Qcr,m,n为支路m,n极限传输约束值。式(17)和式(18)表明，Pm,n,max或Pm,n,min达到或者超出支路最大传输约束Pcr,m,n时，支路有功传输变化量ΔPm,n越大，CBP,m,n越大，该支路功率传输越逼近传输极限边界，支路更脆弱；反之则稳定。同理，当Qm,n,max或Qm,n,min达到或者超出支路最大传输约束Qcr,m,n时，无功吸收变化量ΔQm,n越大，CBQ,m,n越大，支路脆弱趋势更明显。为了使脆弱性指标更加直观明了，将指标进行归一化，即

(19)

(20)

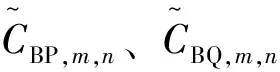
提出CBP，m,n和CBQ，m,n的意义在于结合概率潮流计算中支路传输波动和支路极限传输值来表征脆弱性程度，再综合起来筛选脆弱支路，这样评价结果更能客观反映支路上的荷载情况，更能准确给出支路的脆弱程度。

2.4 基于CGC方法的节点电压概率脆弱性评估

由式(15)中的ΔW(k)可计算得出状态变量ΔX的各阶半不变量ΔX(k)，即

(21)

式中:ΔX(k)由节点电压幅值变化量和角度变化量的各阶半不变量组成，根据节点电压幅值变化量的各阶半不变量可以求出Um的变化范围和概率密度函数(PDF)。

系统实际运行时，节点电压在额定电压值附近随机波动，电压波动的强弱蕴含着实际系统脆弱程度的信息，本文基于概率电压波动范围ΔUm=Um，max-Um，min和系统的临界电压，提出节点电压概率脆弱性评估指标CNU如下：

(22)

式中:U0表示节点m的初始电压值；Ucr,m表示节点m的临界电压值；Um,max和Um,min分别表示系统概率潮流运行中节点m电压的最大值和最小值。同样，也对节点脆弱性指标进行归一化处理，即

(23)

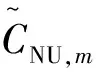
3 计算步骤

考虑风电场随机波动下概率脆弱性评估计算步骤如下：

步骤1：输入风电场相关数据、发电机出力及强迫停运率、负荷的正态和离散分布情况，对风电功率注入的电力系统进行概率潮流计算；

步骤 2：采用连续潮流计算求取不同规模风电场、不同接入点条件下的各个节点和支路的临界电压和极限传输功率值。

步骤 3：计算不同规模风电场、不同接入点条件下的支路脆弱度CBP,m,n和CBQ,m,n，节点脆弱度CNU,m；

步骤4：根据步骤3的概率脆弱性结果确定电网中易脆弱节点和支路；

步骤5：在相同系统运行条件下，将步骤4的结果与传统脆弱性评估结果进行对比，验证本方法的可行性。

4 算例分析

本文采用标准IEEE-30母线系统中加入风电场作为算例，风电场由额定容量为0.6MW的双馈风力发电机组组成，取SB=100MVA，风电机组切入风速、额定风速、切出风速分别为3m/s、13.5m/s、25m/s，风轮直径为54m，额定电压为690V，风电场通过变压器和110kV输电线路接入系统节点，输电线路阻抗参数为12.6+j24.9Ω，定子阻抗为0.004 53+j0.050 7Ω，转子的阻抗为0.004 86+j0.149 1Ω，激磁电抗为2.205 9Ω，风速的weibull模型参数如下：v0=2;k=2;c=11。

4.1 节点概率脆弱性评估分析

将上述风电场分别依次接入IEEE-30母线系统中的各个节点，并进行电力系统仿真，可得到各个节点电压概率波动结果。因为系统中各节点的电压承受能力、无功补偿情况和距离风电场并网点的远近都不一样，所以各个节点是否欠电压或者过电压，以及电压振荡结果也各不一致，当风电场不接入和接入系统末端29号节点时，部分节点电压概率密度函数(PDF)比较结果如图2所示。

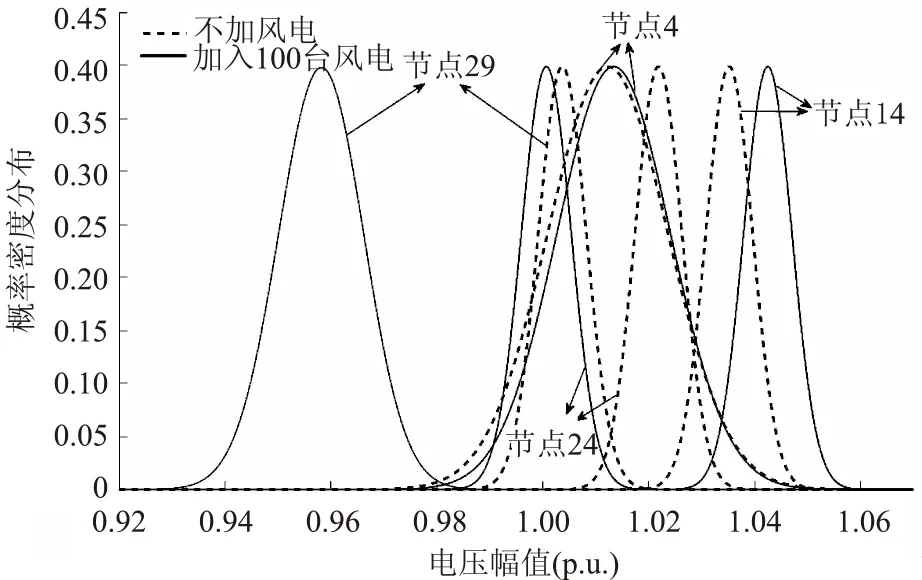
图2 节点电压概率密度曲线比较Fig.2 PDF comparison of node voltage

图2中节点29是与风电场并网点直接相连的节点，节点4和14是远离风电场并网点的节点，与风电并网前的系统对比，节点29的电压振荡范围显著增大，且电压概率密度曲线向电压变小的方向偏移，而节点4的电压概率密度曲线(PDF)基本不变，但是电压波动范围为最大。

系统在不同规模风电场、不同并网点条件下进行连续潮流计算，结果表明当负荷节点为风电并网点时，其临界电压值随着接入风电功率的增强呈上升趋势，电压承受能力增强；反之，其他非并网点的临界电压值基本呈下降趋势，系统的临界值的变化趋势间接影响脆弱性的变化趋势。

由图3可知，当风电场并网于15号节点时，依次接入50台、80台、100台、120台风电机组，节点脆弱性指标值随风电场容量的增加呈递增趋势，表征了节点的脆弱程度会随着风电场规模的增大而愈加脆弱，直至趋于崩溃边缘。这是因为节点电压与无功功率具有高度的相关性，当风电场从电网中吸收的无功功率增大，势必会引起网络中节点电压与能量起伏程度增强。节点3、4始终为脆弱性最强的节点，节点7、9、28为脆弱性相对最弱的节点，节点21～27和节点29～30的脆弱性程度变化幅度显著且各不相同。为更深入地研究节点脆弱性的共性，保持其他条件不变，不同规模大小的风电场分别接入所有负荷节点时的脆弱性曲线重叠如图4所示。根据曲线重叠部分可知，当风电场的装机容量增加时，几乎所有负荷节点的脆弱性指标都有所增强，尤其是节点26、29、30表现出很明显的脆弱趋势。

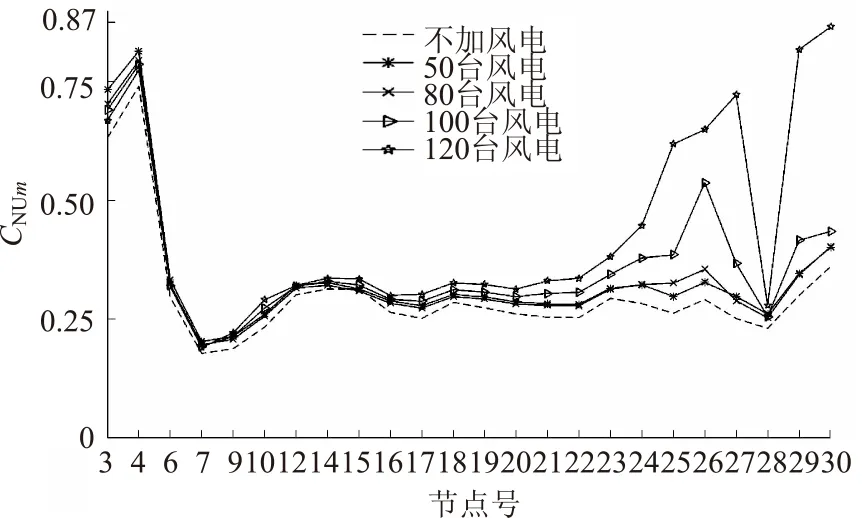
图3 不同规模风电场接入时节点脆弱度曲线比较Fig.3 PDF comparison of node voltage

当并网点分别选在节点3、4、14、15时，系统的节点脆弱程度普遍较为强烈，这是因为节点1、2、5、8、11、13为系统的发电机节点，其功能是向电网注入功率，当风电场并网于发电机附近的这类节点时，增加了发电机节点附近区域的能量传输，且风电场出力具有随机扰动的不稳定性，从而对电网中发电机节点附近节点造成影响，增加了节点脆弱性，对系统稳定性产生进一步影响。当风电场并网点为两个节点时，重复步骤1～步骤4，可得节点脆弱性评价结果如表1所示。

表1 风电场接入两个并网点时的脆弱性评估结果

注：综合脆弱节点为3,4,6,12,14,15,18,24,25,26,27,29,30。

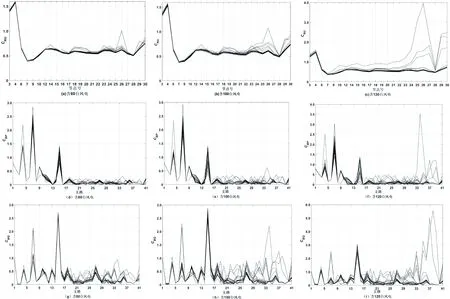
图4 不同规模风电场、不同并网点时脆弱度重叠曲线. (a)-(c) CNU重叠曲线 (d)-(f) CBP重叠曲线 (g)-(i) CBQ重叠曲线Fig.4 Overlapped curves with different wind farm connected to different nodes. (a)-(c) Overlapped curves of CNU ;(d)-(f) Overlapped curves of CBP ; (g)-(i) Overlapped curves of CBQ

由图4(a)-(c)及表1可知，当并网点选为3和15或4和15时，脆弱性节点无变化，当并网点选取15和30节点时，脆弱性节点集中在末端节点。当并网点选在节点29、30时，节点24～30脆弱性指标振荡上升幅度最大，系统后半部分的节点脆弱程度更加恶化。但是系统前半部分节点受到风电场的影响相对较弱，脆弱性不太显著，这是因为节点29和30为系统中带负荷的末端节点，风电场的随机扰动只是对电网末端有影响，对前端和中端电网脆弱性并没有太大影响。

4.2 支路概率脆弱性评估分析

图4(d)中，由80台风电机组组成的风电场分别依次接入所有的负荷节点所得到的支路脆弱性重叠曲线，支路4、7、15脆弱性最大，其次是支路1和9的脆弱性，其余支路的脆弱性在不同接入点轮流切换时表现出比较平缓的波动性，且幅度较小。同理，依次增加风电机组数到100台和120台，重复接入所有负荷节点并进行仿真分析，得到图4(e)和(f)所示的脆弱性重叠曲线，对比发现支路脆弱性随着风电场装机容量的增大呈不断增强趋势，尤其是在风电场增加到120台时，支路34、37、38、39脆弱性显著增加，支路潮流严重越限，逼近崩溃边缘。

同理，根据支路有功脆弱性仿真分析思路，也可得到从无功角度分析支路脆弱性的重叠曲线如图4(g)-(i)所示，对比可知，随着风电场容量的逐渐增大，支路脆弱性呈增强趋势，支路1、4、7、15始终为脆弱性较大的支路，支路33、34、37、38受风电场的波动影响最大，跟随风电机数量增加而脆弱性上升幅度明显，尤其是风电机数量增加到120台时，支路37、38处于崩溃状态，系统支路脆弱性进一步恶化。

当风电场接入两个并网点时，重复步骤1～步骤4，得到的支路脆弱性评估结果与单个并网点时的结果基本一致，综合有功功率指标和无功功率指标可以得到1、2、3、4、6、7、9、10、11、15、33、34、37、38、39、41为共同脆弱性支路，由于4、6、9、27、28号节点为连接变压器的节点，承受着系统中的能量传输负担，风电的接入对系统潮流的分布和运行状态产生更大变化，而更大的能量变化使这些支路承受系统潮流传输中的负担快速加重，表现出更强的脆弱性。距离风电场并网点越近，支路功率潮流数值越大，支路功率所受影响越严重，支路脆弱性越强烈，反之则越弱。

4.3 与支路势能函数法的比较

在同等系统条件下，本文方法与支路势能函数法[13]的评估结果对比如表2和表3所示。

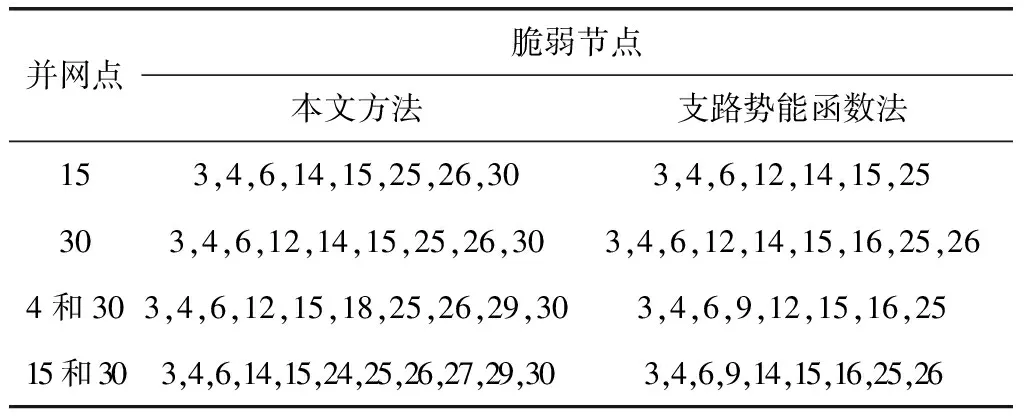
表2 本文方法与支路势能函数法脆弱节点评估比较

通过比较表2、表3的评估结果可得，在相同系统条件下，本文提出的方法的脆弱性评估结果都得到了支路势能法的评估结果，证明了本文方法的正确性。同时验证了节点3、4、6和支路4、7、10、15为固有最脆弱环节。另外，本方法还发现节点27、29、30和支路37、38为潜在脆弱环节。

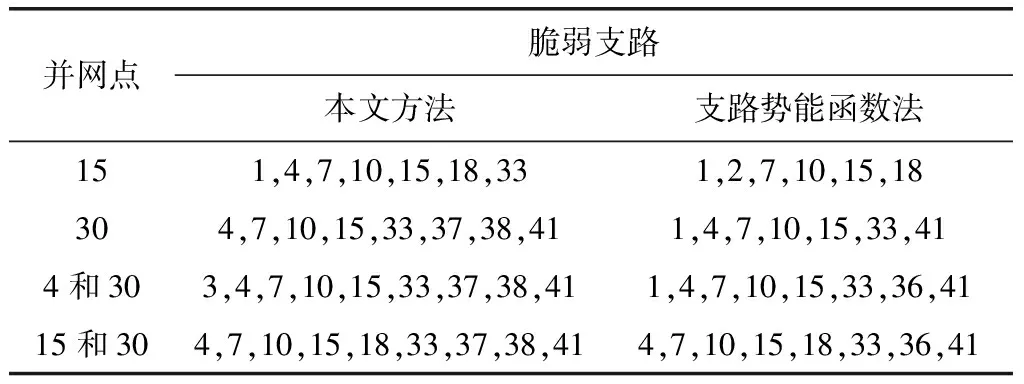
表3 本文方法与支路势能函数法脆弱支路评估比较

5 结 论

本文综合考虑多种内部和外部不确定因素，基于CGC的概率潮流方法，结合系统的临界电压和极限传输功率，提出了评估系统节点和支路脆弱程度的概率脆弱性指标，深入探索了不同规模风电场、不同并网点条件下评估指标的变化，通过在IEEE-30母线系统中进行仿真及与支路势能函数法评估结果进行对比，可得如下结论：

① 本评估指标通过概率来量化风电场有功注入和无功吸收及发电机停运率、负荷的随机波动变化过程，更加全面且准确地凸显了含风电电力系统的各种随机扰动。

② 与传统的脆弱性评估指标进行对比，本指标能够融合随机特性来进行脆弱环节的评估，更接近系统实际运行特性，所提评估指标在脆弱环节处更能呈现出显著特征，且能更准确地筛选出脆弱节点和支路及潜在的脆弱环节。

此外，本文方法能为含风电场的电力系统脆弱性评估人员提供概率脆弱性研究新思路，就此进行更深入完善的研究。