基于IGWO-K-means的风电场动态等值建模

孙元存，刘三明，王致杰，刘 剑，曹天行

(上海电机学院电气学院，上海 201306)

0 引 言

近年我国在风电领域取得了骄人的成绩，2016年，全国新增装机容量23 328MW，占全球市场份额的42.7%；累计装机容量168 690MW，占全球市场份额的34.7%[1]。近年来，风电场建设的规模越来越大，由此带来的安全稳定性问题也越来越多，风电场并网稳定性问题成为了研究热点，首当其冲的便是风电场等值建模问题[2]。

风电场所受影响因素较多，故建立详细的模型比较困难，此时就需要对风电场进行简化建模[3]。风电场等值建模可以分为单机和多机等值法[4]。当风机对应的风速差异较小时，可用单机等值法。但当风机对应的风速差异较大时，单机等值法就不适用了，此时需要使用多机等值法对风电场进行分群聚类建模，达到与实际模型更为接近的效果。对此不少学者深入研究了风电场分群聚类。

在聚类指标选取方面，文献[5]选取了13个中间状态变量，全面地分析了双馈异步机的数学建模，但很多变量在实际操作过程中难以获得，在实际风电场建模中难以推广。文献[6]考虑了尾流效应、风速和风向的影响，但考虑的因素不够全面。文献[7]定义了尾流效应因子，但仅仅考虑了尾流效应的影响。

在多机等值聚类方面，聚类算法成了研究的热点。K-means算法因其对聚类数目和聚类中心的依赖使其在使用时需结合其他算法来提高其稳定性。文献[8]提出以分裂层次半监督谱聚类对风电场机组进行划分。文献[9]基于改进H-K聚类来寻求最佳聚类数。文献[10]和[11]提出了基于模糊C均值聚类算法，聚类效果有了很大的提升。文献[12]提出了基于敏感初始中心和免疫离群数据改进K-means算法的风电场机组划分方法，提高了聚类精度。文献[13] 结合粒子群算法，定义了一种不需要迭代的方式，对初始聚类中心优化。文献[14]采用灰狼优化并结合K-means算法寻优聚类。

本文针对风电场等值建模中聚类指标选取和聚类中心优化问题，从两方面研究。一是基于风、风机本体、风电输出效果和风机工作环境等4个方面，从内蒙古某风电场实际采样的运行数据中选取了14个变量作为分群指标；二是提出了收敛因子非线性策略和动态参考率策略两个控制策略，改进了灰狼优化算法(GWO)，提高了灰狼优化算法的搜索精度和速度，并结合K-means聚类算法寻找最佳聚类中心，输出聚类结果。利用IGWO-K-means算法将风电场内的机组进行聚类，进行风电场等值建模；最后在Matlab/Simulink中搭建模型，仿真验证分析。

1 改进灰狼优化算法(IGWO)

1.1 灰狼优化算法数学模型

(1)

式中:t表示当前迭代的次数;Gp是猎物位置;G是灰狼位置;Ai是距离系数，当|Ai|>1时，狼群全局搜索；当|Ai|<1时，狼群局部搜索。Di表示狼群到猎物之间的距离。距离可以表示为

(2)

式中:Ci是位置系数。

(3)

式中：r1、r2是[0,1]之间的随机数；a是2到0的线性下降。

(4)

当灰狼判断出目标猎物的位置时，由α狼指导，β狼、δ狼也参与其中指挥其他ω狼捕猎。ω根据α狼、β狼、δ狼的相对位置来判断目标猎物的相对位置，并且不断更新自身的位置，具体描述如下[18]：

(5)

式中：Gα(t)、Gβ(t)、Gδ(t)分别代表α、β、δ当前的位置；C1、C2、C3与C的含义相同。

(6)

G(t+1)=G1+G2+G3

(7)

式中：G1、G2、G3分别代表灰狼相对α、β、δ的位置；G(t+1)表示ω最终的位置。

1.2 灰狼优化改进策略

K-means算法收敛快，但不稳定，会受到聚类中心的影响而造成结果差异巨大。而灰狼优化算法有着强大的全局和局部搜索能力，而本文想进一步提高搜索的精度和速度，故提出两个策略来改进灰狼优化。

1.2.1 收敛因子非线性策略

灰狼优化中a是2到0的线性下降，但收敛过程却不是线性下降的，本文提出非线性策略来提高狼群的搜索能力。其思想是在搜索过程初期加强全局搜索的能力，降低衰减程度；在后期加强局部搜索能力，加强衰减程度[19]。这样避免了在整个搜索过程中衰减程度一成不变，也加强了灰狼的搜索能力。本文提出非线性收敛方式为

(8)

1.2.2 动态参考率策略

灰狼优化中，对于ω狼，其迭代方式是G(t+1)=G1+G2+G3。但在灰狼优化中，α狼作为最优解，所以整个搜索过程对α狼的依赖率比较大，故本文引进参考率Ri作为ω狼对于其他3种狼位置的参考，不断调节权重，动态调节搜索能力。本文提出的参考率如下：

(9)

式中：R1、R2、R3是ω狼对α狼、β狼、δ狼位置相对应的参考率，最终迭代为

G(t+1)=R1G1+R2G2+R3G3

(10)

本文提出收敛因子非线性策略和动态参考率策略来提高搜索精度，以便寻找到最佳聚类中心。再结合K-means聚类算法，得到最终聚类结果。

2 风电场多机等值建模

2.1 聚类指标的选取

将同调等值法借鉴到风电场等值建模中[20]，风电机组的运行特性用分群指标来表示，将运行特性相近的风电机组等值为同一台机组，提高运算速度，同时又接近实际运行的精度。本文根据内蒙古某风电场内24台1.5MW双馈异步风电机组，从该风电场的SCADA系统中直接获取实际运行数据，建立了24×14维的数据样本X(n×b)=[X1,X2,…,Xn]，n代表风机的数量，n=24；b代表指标个数，也就是样本矩阵的维度，b=14 。选取的分群指标是风电场易获得的采样数据，同时又能全面地描述风电场运行特性。

首先从风的角度去考虑，选取风速v和风向o作为分群指标；其次从风机本体的角度去考虑，选取发电机转速ω，风机转子转速r和叶片角度γ作为分群指标；然后从风机输出效果的角度去考虑，选取输出有功功率P，机端电压的有效值u1、u2、u3，输出电流的有效值i1、i2、i3和功率因数θ作为分群指标；最后从风机工作环境的角度去考虑，将机舱工作环境温度F作为分群指标。综合看来，本文选取v,o,ω,r,γ,P,u1,u2,u3,i1,i2,i3,θ,F等14个状态变量作为分群指标。从4个方面考虑，避免了指标单一化而造成的分群产生误差；同时采样的运行数据又是从风电场的SCADA系统中直接获得，简便易得。这样既降低了等值建模的难度，又提高了等值建模的精度。

2.2 等值模型参数计算

假设有n台机组聚类成一台，各部分等值参数如下[21]。

2.2.1 发电机参数

(11)

式中：Seq为等值后容量;Peq为等值后有功功率;Qeq为等值后无功功率;Xeq为等值后发电机励磁电抗;Rseq为等值后定子电阻;Rreq为等值后转子电阻;Xseq为等值后定子电抗;Xreq为等值后转子电抗。

2.2.2 轴系参数

(12)

式中:Hgeq为等值发电机转子惯性时间常数;Hteq为等值风力机时间惯性常数;Kseq为轴系刚度系数。

2.2.3 电容器和变压器参数

(13)

式中:Ceq为等值补偿电容;STeq为等值变压器容量;ZTeq为等值变压器阻抗。

2.2.4 集电系统参数(风电机组采用放射式接入)

(14)

式中:Zeq为等值电缆阻抗。

2.3 基于IGWO-K-means等值建模

采取上述风电场中现场采样的数据为样本数据，将上述风电场24台1.5MW双馈异步风电机组的14个状态变量v,o,ω,r,γ,P,u1,u2,u3,i1,i2,i3,θ,F等作为分群指标。设定分群聚类后每一类中所有数据到该类中聚类中心的距离和为目标函数，目标函数值最小，则找到最佳聚类中心。目标函数为

(15)

式中：yi是第i类中的聚类中心;K是聚类数;xij是第i类数据对象;f是目标函数的适应值。要求目标函数的适应值最小，不断的更新α狼、β狼、δ狼的位置，找到目标函数最小的适应度，最后得到最优解α狼迭代情况，也是最佳聚类中心。本文提出的IGWO-K-means算法具体过程如下：

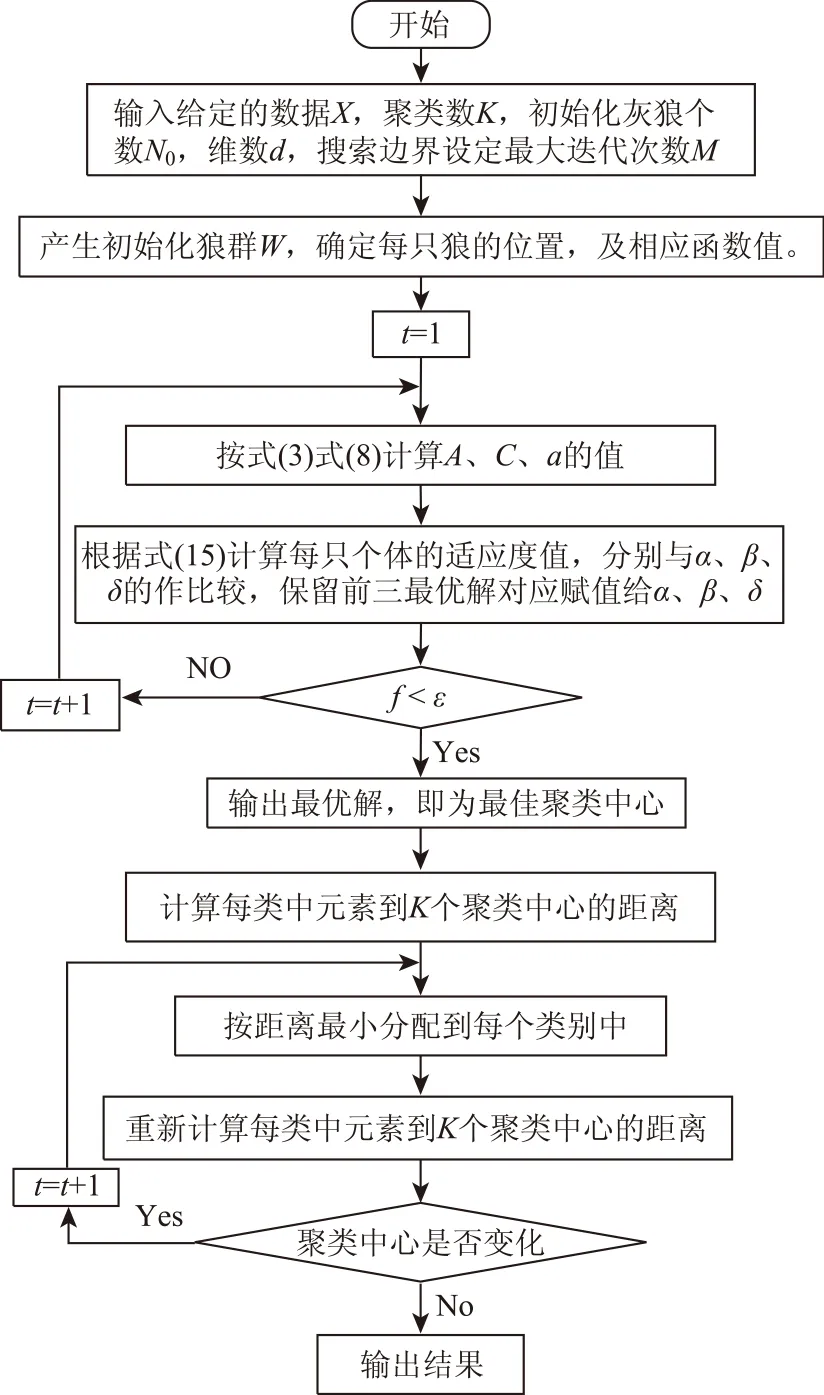
图1 IGWO-K-means算法流程图Fig.1 IGWO-K-means algorithm flow chart

验证实验的数据采用的是上述风电场实际采样运行数据，数据样本为24×14维，设置每个算法里的种群数为50，也就是灰狼个数为50只，算法的最大迭代次数为1 000。bl(变量变化的下限)中元素全为0，bu(变量变化的上限)中元素全为1。根据实际要求取聚类数为4，即聚类中心有4个。

得到最终IGWO-K-means算法的聚类结果为4类，分类结果如表1所示。

表1中每一类别中有不同的机组数，代表将原来24台机组聚类成4类，每一类中分别有3、6、8、7台机组。此时将风电场等值成4台机组，每台机组的容量不等，分别是4.5MW、9MW、12MW、10.5MW。

表1 聚类结果

接着将本文算法与其他算法对比，都选取本文提出的分群指标。实验中的平均值、标准差是通过50次独立实验得出的。将适应度的值设置为7.4，若小于或等于7.4 则说明该实验达优，达优率为独立实验中满足优秀的条件的概率。

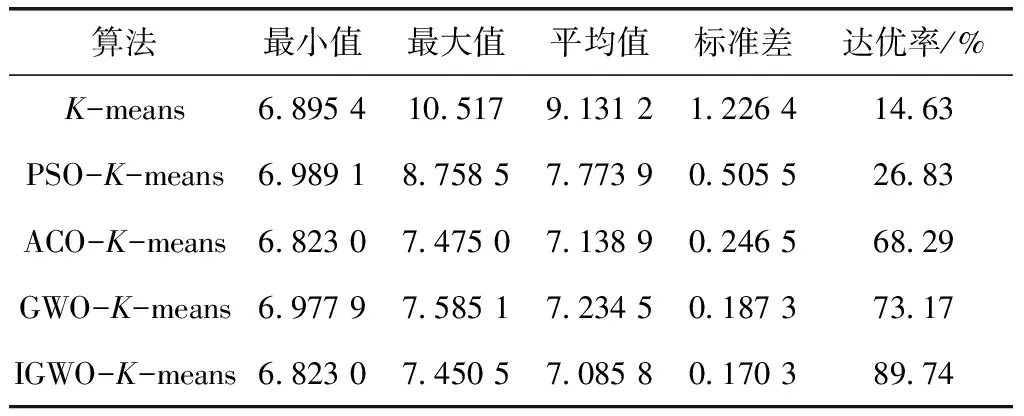
表2 各算法实验结果

由表2得出，K-means虽然迭代收敛速度快，但极其不稳定。因为聚类中心的选择不同反映出来的各项指标都差。粒子群(PSO-K-means)算法相比于K-means，稳定性和达优率有了一定的提升，但效果还太不理想。蚁群(ACO-K-means)算法的稳定性又进一步提升了，而且达到最佳适应度值的能力也比前两种算法的能力强。GWO-K-means算法的聚类精度以及稳定性都较K-means和PSO-K-means有了极大的提升和ACO-K-means类似，但是稳定性以及达优率比ACO-K-means要好，这说明GWO-K-means的寻优能力较强而且稳定。IGWO-K-means在表1中的各个指标都是最好的，值得突出说明的是达优率比其他算法都有质的提升。说明IGWO-K-means的寻优能力很强，聚类精度高，并且极其稳定。

3 仿真算例分析

在Matlab/Simulink中搭建风电场并网模型。风电场装机总容量为36MW，含24台1.5MW的双馈风电机组，分别经过0.69/35kV升压变压器，再经过35/220kV馈线接入电网。从有功功率、无功功率和电压3个方面分析。风况为风电场随机获得的风速，每台风机的风速不等，具有一定的随机性。在1s时系统设三相短路故障，1.05s后故障清除。

3.1 本文模型与按风速聚类模型对比分析

基于同样的聚类分群算法，对比不同分类指标的选择优劣。对比按风速聚类指标模型和本文提出的聚类分群指标模型。从有功功率、无功功率、电压3个方面来仿真分析。

① 有功功率

由图2所示，为几种模型输电线路有功功率对比仿真曲线。

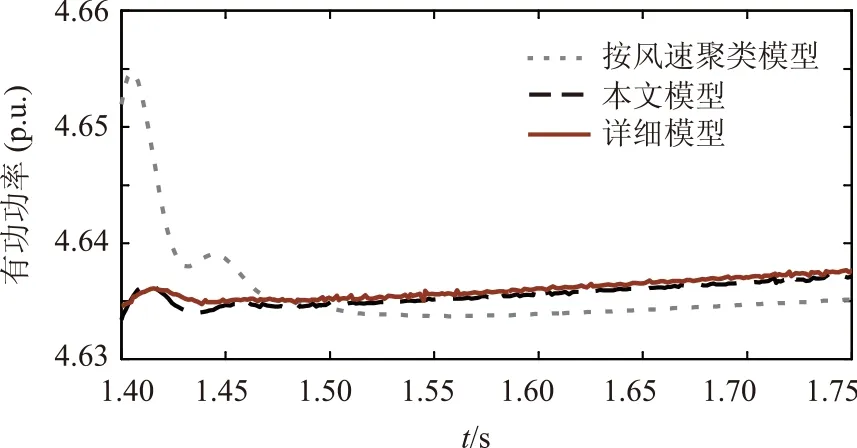
图2 线路有功功率局部放大图Fig.2 Partially magnified comparison of active power

② 无功功率

由图3所示，为几种模型输电线路无功功率对比仿真曲线。

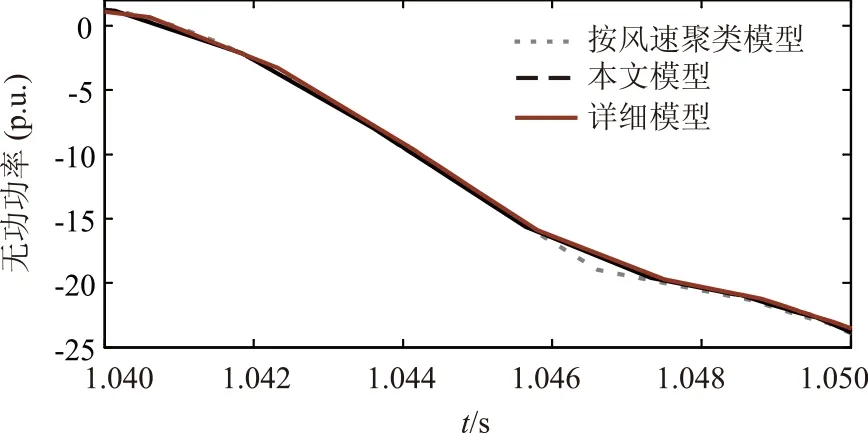
图3 线路无功功率对比局部放大图Fig.3 Partially magnified comparison of reactive power

③ 电压

由图4所示，为几种模型系统并网口电压对比仿真曲线。

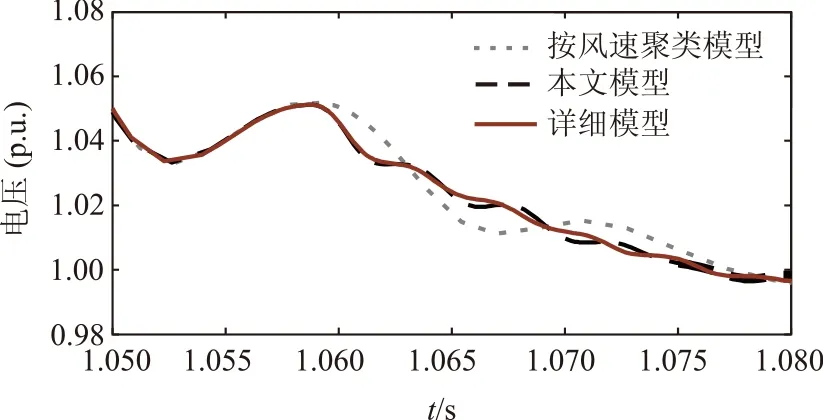
图4 并网口电压对比局部放大图Fig.4 Partially magnified comparison of port voltage

由图2到图4所示，本文所建的模型与实际详细模型曲线比较贴近，而按风速聚类模型与实际详细模型差距相对较大，由此可以看出本文所建模型的合理性。

比较两个模型对实际详细模型的相对误差，见表3。

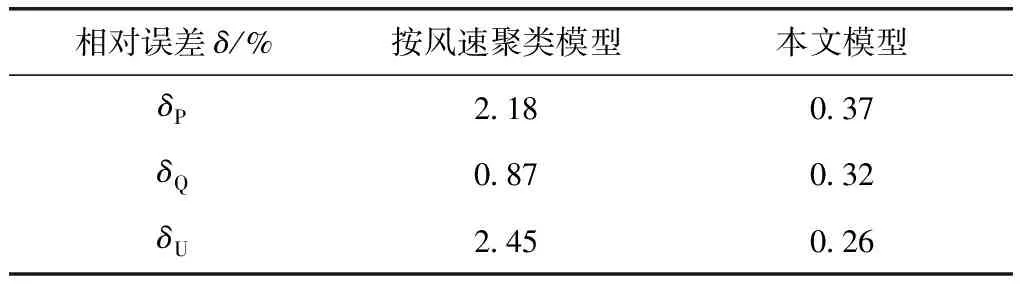
表3 本文模型和按风速聚类模型对详细模型相对误差

δP、δQ、δU分别是风电场并网后有功功率、无功功率、并网口电压相对误差的百分比，对比将风速作为分群指标和本文所选分群指标，都使用改进的灰狼优化算法，由表3可以看出，本文所建模型的相对误差远远小于按风速聚类的模型的，说明本文选取的以风电场实际运行状态数据为聚类指标是合理的，而且与实际的详细模型比较贴近。

3.2 基于IGWO-K-means模型与基于其他算法模型对比

基于上文所做的实验，对比用不同算法聚类和本文提出的算法，将各算法出现次数最多的聚类结果作为该算法最终的分群结果。同样从有功功率、无功功率、电压3个方面来仿真分析。

① 有功功率

如图5所示。

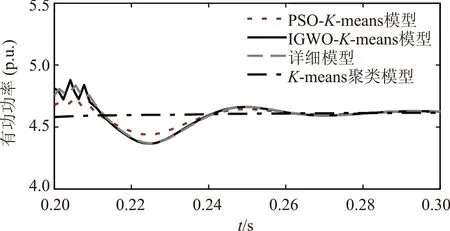
图5 线路有功功率对比局部放大图Fig.5 Partially magnified comparison of active power

② 无功功率

如图6所示。

图6 线路无功功率对比局部放大图Fig.6 Partially magnified comparison of reactive power

③ 电压

如图7所示。

由图5～图7可以看出，本文所建的模型即基于IGWO-K-means模型与实际详细模型曲线几乎重合，而基于PSO-K-means模型与实际详细模型差距相对较大，基于K-means模型与实际详细模型差距最大，由此可以看出本文所建模型的合理性。

比较各个算法模型对实际详细模型的相对误差，见表4。

表4 各个算法模型对实际详细模型的相对误差

由表4可以看出，本文所建基于IGWO-K-means模型的相对误差都远远小于其他算法模型的，说明本文采用基于IGWO-K-means算法优化聚类中心的效果好。

4 结束语

本文以风电机组实际运行状态数据为分群指标，从风(风速和风向)、风机本体、风机输出效果、风机工作环境4个方面考虑，避免了指标单一化而造成的聚类产生的误差；同时运行状态数据又是直接从风电场采样获得，操作起来方便。这样既降低了等值的难度，又提高了等值建模的精度。

其次建立了每一类别中的所有数据到该类中聚类中心距离和最小的适应度函数，提出了收敛因子非线性策略和动态参考率策略，将收敛因子a的线性下降优化成非线性下降策略，将ω狼等量的迭代方式优化成动态的对每个狼依赖的迭代方式，以便提高灰狼优化算法的搜索精度。

然后采用改进的灰狼优化结合K-means算法(IGWO-K-means)优化聚类中心，再进行聚类，结果证明本文模型与实际详细模型的差距较小，本文提出的模型分群效果好于其他算法，适用于风电场等值建模。