基于时空分布负荷预测的电动汽车充电优化

周凌锋，王 杰

(上海交通大学电子信息与电气工程学院， 上海 200240)

0 引 言

近年来,为了应对日益严重的环境污染问题和能源短缺问题,电动汽车获得了快速的发展[1-3]。美国计划在2015年之前拥有100万辆电动汽车[4]。大规模电动汽车接入电网可能会对电网负荷产生冲击，引起电能质量下降[5]。另一方面，由于电动汽车充电具有可断续充电的特点(充电“弹性”)，为其充电的优化提供了可能。若有效利用，电动汽车也可以为电网提供诸如削峰填谷、调频等作用[6]。

为了减少电动汽车无序充电对电网造成的损害，近年来，国内外对智能充电调度优化进行了大量研究。文献[7]提出了一种考虑电动汽车分散式充电的最优填谷优化策略，在考虑用户竞争的情况下，有效抑制了峰谷差。文献[8]考虑了电动汽车的充电和放电过程，提出了全局最优和局部最优的充电优化策略。文献[9]将电动汽车作为一个群体，以集群最优削峰填谷为目标提出优化方法。文献[10]研究了分时电价影响下的集中充电策略。但是它们都没有考虑用户用电的时空分布特性，对电动汽车开始充电时刻以及初始电量也未给出预测信息。电动汽车充电负荷的时空分布特性与负荷预测信息是研究电动汽车对电网设施影响与控制策略的重要组成部分。由于电动汽车用户充电行为受时间和空间的不确定性影响，预测电动汽车的负荷需求难度较大。文献[11]利用模型仿真的方法，构建了电动汽车充电负荷时空分布模型。文献[12]通过历史统计数据，得到了电动汽车充电负荷的时空分布。文献[13]提出了一种基于电动汽车驾驶、停放特性的充电负荷时空预测方法。文献[14]提出了基于居民出行链的充电负荷时空分布模型。可见，准确预测并给出充电时空分布模型对于电动汽车的充电优化调度至关重要。

本文首先提出了一种基于马尔可夫链的电动汽车时空分布负荷预测模型。该模型综合考虑了居民区、商业区与工业区不同的负荷信息，同时给出了电动汽车接入电网的时刻和初始荷电状态信息。基于预测模型，本文提出了一种集中式的削峰填谷优化方法。在具体算例中，本文还考虑了SOC阈值对优化结果的影响。

1 马尔可夫链预测时空状态转移

电动汽车的时空转移过程是随机离散的过程。马尔可夫链是一种用来描述离散随机过程的预测方法，具有无后效性[15]的特点。无后效性是指未来状态与历史状态无关，仅与当前状态及状态转移概率有关。在马尔可夫链中，状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率。马尔可夫链一般用一个条件分布概率来表示。假设当前时刻t的状态为Si，t，下一时刻的状态为Sj,t+1,pij,t为t时刻从状态Si,t转移到状态Sj，t+1的概率，马尔可夫链可以用条件分布概率表示为

pij，t=p(Si,t→Sj,t+1)=p(Sj,t+1|Si,t)

(1)

电动汽车一天中的状态主要有两种：即行驶状态和停车状态。而停车状态又与不同的行驶目的地有关。若将电动汽车行驶目的地进行分类，并视为一个行驶状态，根据马尔可夫理论，下一个行驶状态只与当前行驶状态有关。本文主要考虑3类行驶目的地，即住宅区、商业区和工业区。任一个时刻t电动汽车共有4个行驶状态：行驶中(SM,t)，在住宅区(SR,t)，在商业区(SC,t)，在工业区(SI,t)。根据马尔可夫原理，对于任意时刻t处于状态Si，t的电动汽车，下一时刻只能由当前状态转移到其余状态中的任意一个，因此，针对任意一个行驶状态i,转移概率满足：

∑pij,t=p(Si,t→Sj,t+1)=1

(2)

对于任意时刻t，电动汽车从一个行驶状态转移到另一个行驶状态的状态转移概率矩阵为

(3)

由式(2),我们知道矩阵Pt中的每一行相加的和为1。其中pij,t可以根据居民出行统计数据得到。

图1描述了本文提出的马尔可夫链状态转移关系模型。在我们提出的马尔可夫链中，不存在停车地点之间的直接转换。不同停车地点之间的状态转移是通过行驶状态进行转换的。需要特别指出的是，本文认为PMM,t为零，即不存在从一个行驶状态转移到另一个行驶状态的过程。行驶过程中的行驶距离可由时空距离分布模型计算得出。

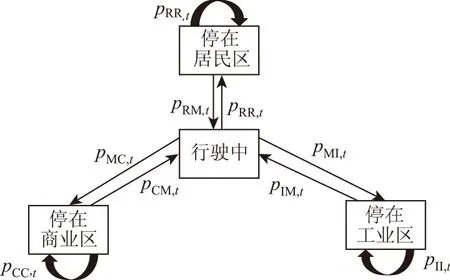
图1 电动汽车时空分布状态转移马尔可夫链Fig.1 Markov chain of electric vehicle with spatial and temporal distribution state

2 电动汽车时空负荷预测方法

2.1 初始状态和状态转移概率

为预测电动汽车负荷的时空分布，需要确定两个方面：电动汽车初始状态和状态转移概率矩阵。本文以小时为单位进行预测，在优化充电中主要考虑夜间充电。参照文献[16]中的统计报告,在夜间12时，电动汽车的初始状态如下：89%停留在家中，4%停在商业区，2%停在工业区，5%处于行驶状态。

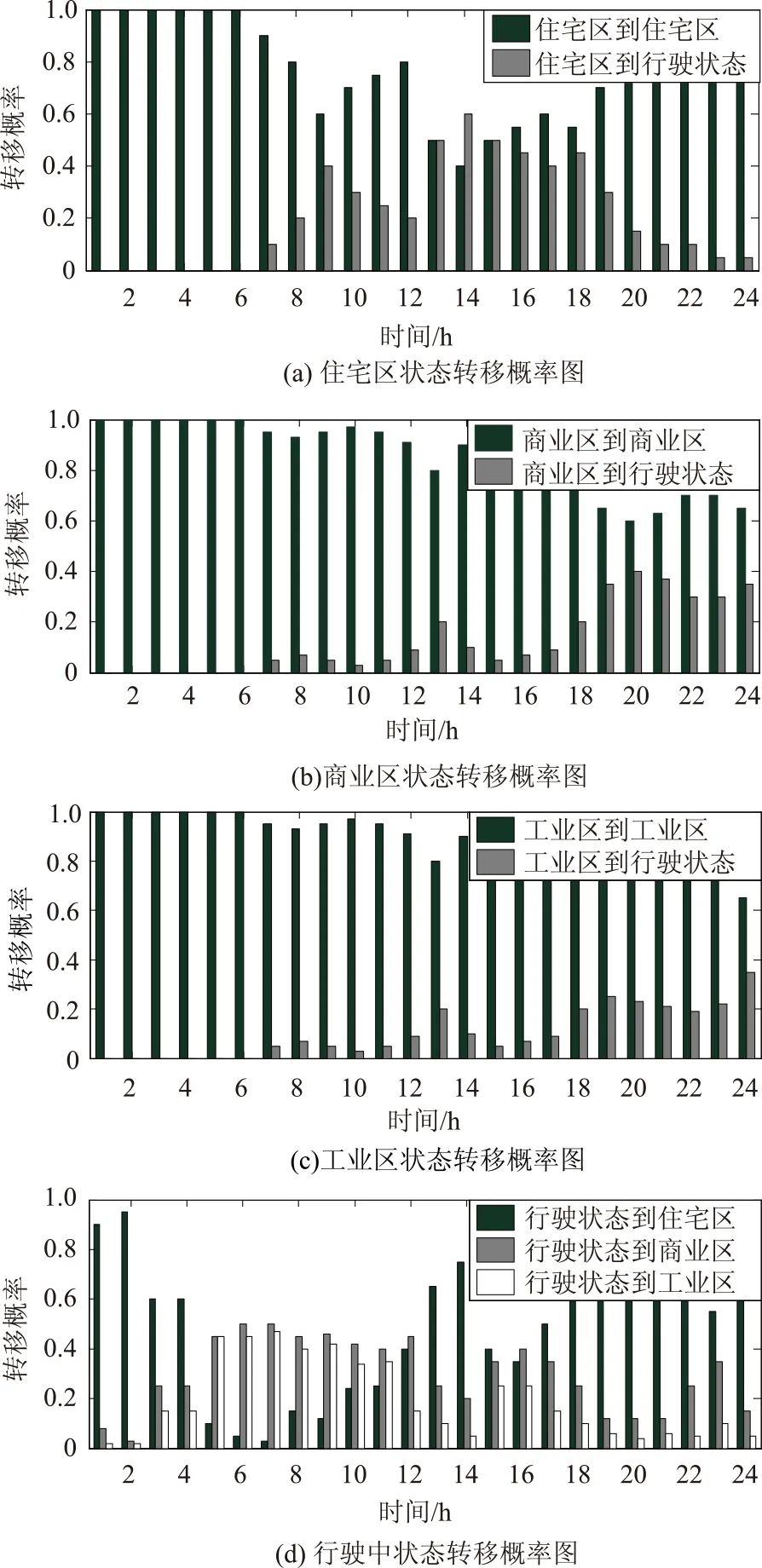
图2 电动汽车状态转移概率Fig.2 State transfer probability of electric vehicle

图2给出了电动汽车一天24h的状态转移概率。根据初始状态和状态转移概率，可以得到电动汽车充电的时空分布。根据图2，在夜间0:00—上午9:00，住宅区、商业区和工业区的车都基本不再行驶，可以依据其荷电状态在夜间对电池进行充电。

2.2 电动汽车充电需求时空分布计算

根据居民出行日行驶里程及每公里耗电量可以得到电动汽车SOC值。由于电动汽车目前发展规模不大，相关行驶距离数据较缺乏，故一般用传统燃油车的统计数据代替分析。其中，美国家庭交通出行调查数据(NHTS)是具有代表性的调查数据。分析数据可得，每段行程行驶里程可近似为对数正态分布[14]，概率密度函数为

(4)

式中：d为每段行程行驶距离;μD为行驶距离期望值;σD为行驶距离标准差。本文中以每段行程距离为分析数据;μD取值3.7km，σD取值0.9[13]。

目前大多数文献都只考虑一天充一次电的模式[7,10]。实际问题中，充电与否取决于剩余电量能否完成下一段行程。同时为了保护电池寿命，一般电池容量低于20%时需要充电，20%称为SOC充电阈值。本文中，电动汽车行驶到目的地k的充电决策条件为

(5)

式中:Sk为行驶到第k个目的地剩余的SOC值;C为电池容量;α为每公里耗电量;lk为第k段行程的距离。由于考虑了多次充电，在马尔可夫预测模型中，采用双层仿真预测模型。第一层先预测并计算出每辆车的出行链时空分布。第二层再由出行链时空预测结果进行充电决策，最终得到不同时空区域的电动汽车用电负荷分布。本文采用蒙特卡洛模拟得到充电需求，仿真流程如图3所示。

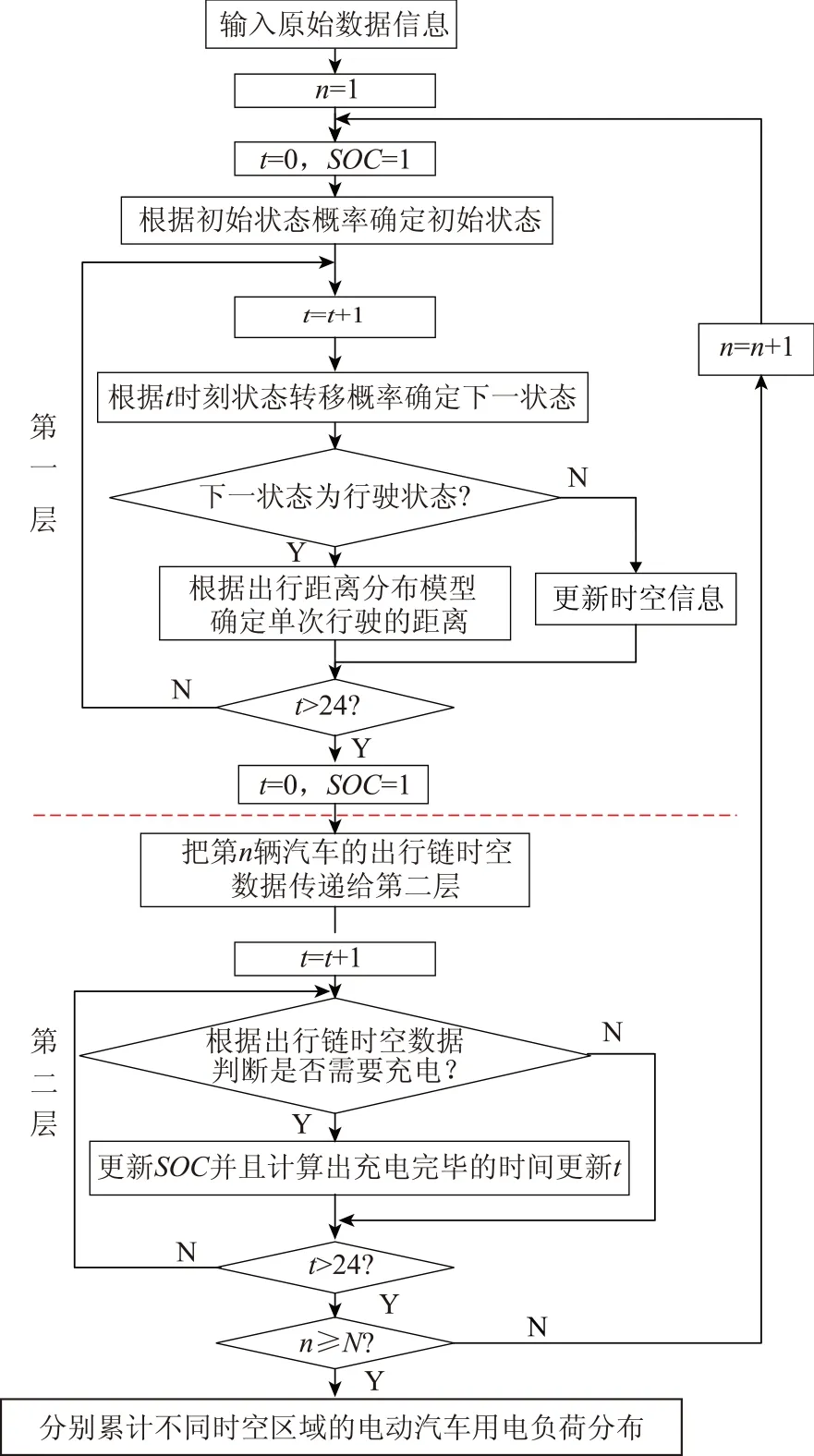
图3 基于蒙特卡洛模拟的双层充电负荷预测流程图Fig.3 Flow chart of double layer charging load forecasting based on Monte Carlo simulation

系统的输入有：电动汽车仿真总数N，车辆电池容量和充电功率水平以及每公里耗电量。先根据初始状态概率和概率转移矩阵得到每辆车的出行链时空分布，然后将此分布数据传递给第二层。第二层根据式(5)来确定充电的决策与SOC值的计算和更新。最后累计得到不同区域的用电负荷分布。

3 电动汽车充电优化

3.1 电动汽车优化模型

假设电动汽车结束一天行程之后需要充电，第二天出门时电量需充满。为了避免电网负荷的晚高峰，减少电网的网损，需要对电动汽车的充电策略进行优化调度。本文主要考虑夜间电动汽车的充电优化。夜间的优化策略同样可以应用于电动汽车日间充电的优化。

考虑夜间充电时段(20:00到次日09:00)。假设一共有N辆电动汽车需要充电。在时间段[1,T]内，仿真步长为Δt。由于在0:00—9:00之间电动汽车近似不行驶，所以在夜间充电时段，电动汽车入网时刻的区间为20:00—0:00。假设第n辆车的入网时刻为tn,in，tn,in即为一天行程结束的时间，可由图3中第一层预测的出行链时空分布确定。第n辆车额定充电功率为rn,充电需求为Rn。时刻t的实时充电最优模型[7]为

(6)

(7)

式中:D(t)为时刻t电网其他负荷的和(基荷);η为入网电动汽车集合;rn(t)为第n辆车时刻t的充电功率;rn,max为第n辆车的最大充电功率。函数U(x)为一个严格凸性的函数，可以保证负荷以严格填谷为目标[7]。在每个时间步长Δt内， 实时充电模型更新充电需求，充电电量及总负荷信息。

3.2 电动汽车优化算法

充电优化方法主要有集中式优化方法(把所有电动汽车视为一个整体优化)和分布式优化方法(对每个汽车个体分别优化)。一般来说，集中式优化方法的收敛速度更快[7]。本文采用一种集中式优化算法来对电动汽车充电进行优化。

集中式充电策略要求有集中式的管理设备与电网进行信息交互，由控制设备给出每辆车的充电策略，再由能量管理系统传给每个充电柱，以达到充电优化的目的。

本文中提出的基于进化算法的集中式优化算法的流程图如图4所示。

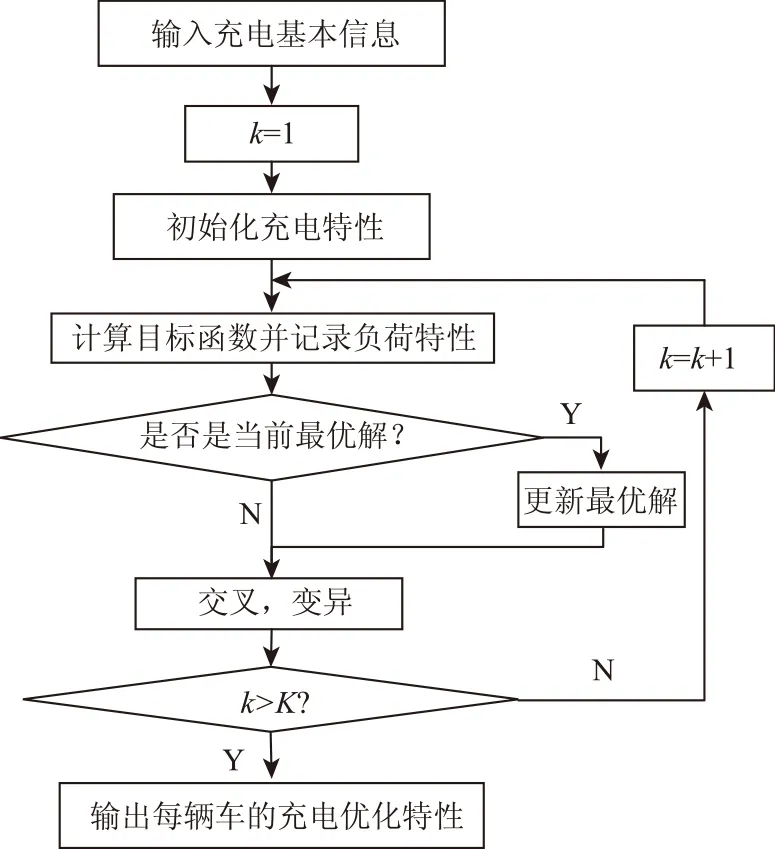
图4 基于进化算法的电动汽车充电优化算法流程图Fig.4 Flow chart of electric vehicle charging optimization algorithm based on evolutionary algorithm

输入：车辆总数N，规划时段[1,T],每个时刻基本负荷D(t)，每辆车的充电需求Rn，第n辆车的最大充电功率rn,max，算法总循环代数K。

输出：每辆车的充电特性rn=(rn(1),…,rn(T))。

第一步：初始化每辆车的充电需求特性，同时对于∀n∈N,∀t∈[1,T]，rn(t)=0 ，循环次数k=1。

第二步：计算目标函数(6)，并记录负荷特性。

第三步：采用精英策略，判断是否是当前最优解。

第四步：利用步骤2中得到的负荷特性，进行交叉和变异，得到下一代。

第五步：k=k+1，回到第二步，直到k=K。

4 算例分析

为了验证本文研究的有效性，采用如表1所示的基本参数进行算例分析。

根据国家标准《电动汽车传导充电用连接设备》规定，电动汽车有交流和直流两种接口充电方式[13]。假设居民区车辆以额定电压250V、额定功率4kWh充电，工商业区以额定电压440V、额定功率14.1kWh充电。选择充电的SOC阈值可调节。

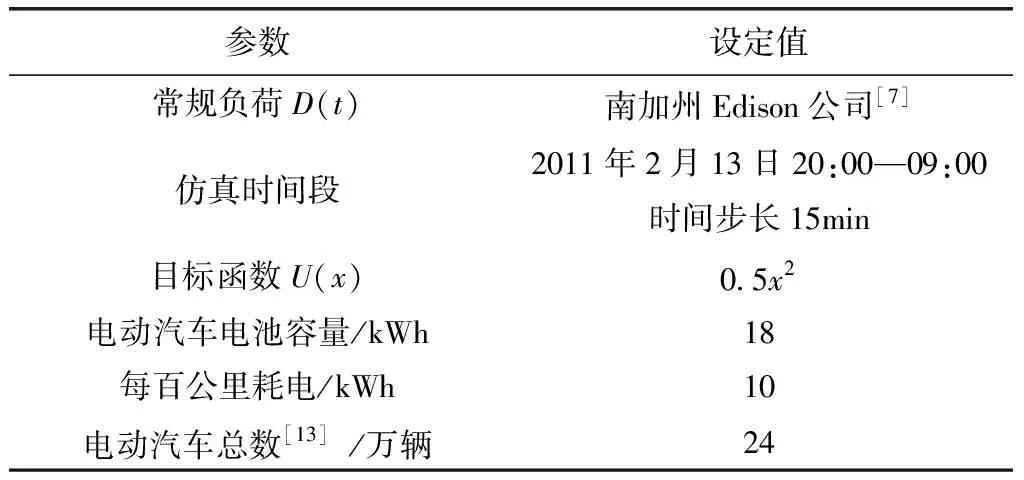
表1 算例参数设计Tab.1 Parameters of case study

4.1 基于用户用电习惯的负荷充电优化

居民夜间充电入网时间受SOC阈值和充电设施配备率影响。假设SOC阈值为20%，用户夜间充电入网时间取决于用户用电习惯。本文认为用户在电量低于SOC阈值时马上充电。电动汽车的负荷时空分布和优化的夜间充电结果如图5所示，对应的夜间电网总负荷结果(标幺值)如图6所示。

图5 基于用户用电习惯的负荷时空分布Fig.5 Load spatial and temporal distribution result based on user’s behavior

由图5可知，白天住宅区充电高峰在12:00，商业区和工业区大概集中在下午2:00。对于大部分用户来说，由于用电习惯，在SOC小于SOC阈值时即开始充电，所以住宅区的负荷在白天是3处充电场所中峰值最小的，但晚上却是3处中峰值最大的，并且晚上的峰值负荷超过了白天任何地点的峰值负荷。优化充电策略可以减少夜间充电峰值，将夜间充电负荷峰值减小并“后移”，减少了夜间充电的波动。图6中展示了基于用户用电习惯负荷分布情况和理论最优值之间的差距。可以发现，基于用电习惯的充电方式本质上是一种“无序”的充电方式，与最优填谷值差距较大。

图6 基于用户用电习惯的夜间电网总负荷Fig.6 Total load of power grid at night based on the user’s behavior

4.2 不同SOC阈值下的负荷充电优化

本文假设住宅区，工业区和商业区都100%配备了充电设施，且不存在竞争现象，用户充电没有充电排队时间。图7为SOC阈值分别为0.2,0.5,0.8时的负荷分布情况。可以看到，随着SOC阈值的升高，白天的充电负荷峰值会略微增大，晚上的充电峰值会下降。这是由于随着SOC阈值的上升，电动汽车的续航能力下降，需要充电的次数增加。使得大部分汽车在白天特别是中午的充电需求变高，而在夜间结束一天行程时，剩余的SOC容量较大，充电需求减小，所以对应的夜间电网峰值减小。不同SOC阈值下的夜间电网总负荷结果(标幺值)如图8所示。

图7 不同SOC阈值下的负荷时空分布Fig.7 Load spatial and temporal distribution under different SOC threshold

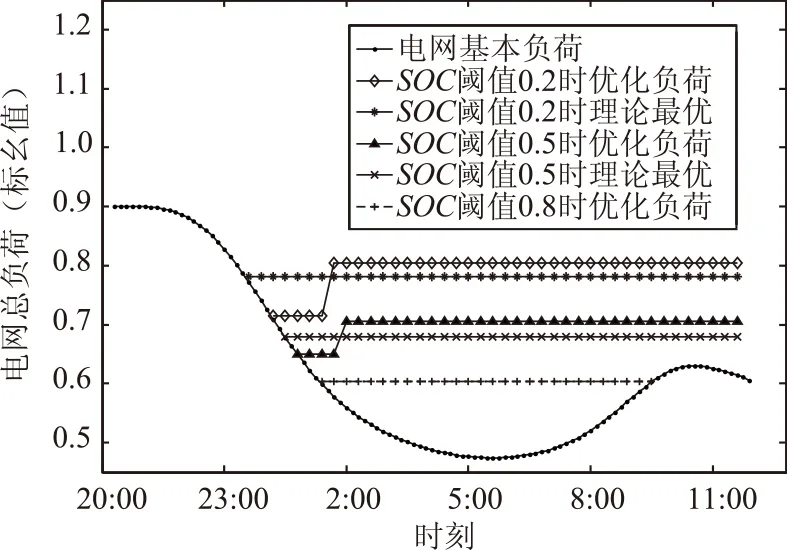
图8 不同SOC阈值下的夜间电网总负荷Fig.8 Total load of power grid at night under different SOC threshold

可以看到，不同SOC阈值对应的优化结果不同。随着SOC阈值的上升，夜间充电需求下降，对应的理论最优曲线也随之变化。由于本文采用的是实时优化的填谷模型，在每一时刻只考虑已入网汽车的优化，所以在算例中，当SOC阈值为0.2和0.5时，优化负荷曲线和理论最优曲线有一定偏差(因为理论最优的填谷起始时刻在最后入网汽车的时间之后)。当SOC阈值为0.8时，此时由于理论最优的填谷的起始时刻在12点(最晚汽车入网时间)之后，优化负荷曲线和理论最优填谷曲线重合。

5 结束语

①基于马尔可夫链状态转移概率模型预测电动汽车负荷的时空特性分布曲线。通过设置中间状态(汽车行驶状态)连接了住宅区、商业区和工业区的充电地点转移问题。考虑了更接近实际的多次充电情景，通过双层蒙特卡洛模拟预测模型建立了电动汽车的时空负荷预测模型。

②针对电动汽车夜间无序充电使电网负荷峰值增大、网损增加的问题，提出了一种基于进化算法的电动汽车实时充电优化算法。降低了夜间的电网峰值负荷，实现了夜间充电的最优填谷。

③考虑电动汽车不同充电SOC阈值对电网负荷的影响，发现随着SOC阈值增大，夜间最优填谷下移。为得到较好的填谷效果，可适当增大充电的SOC阈值，使最优填谷曲线与优化负荷曲线重合。

④本文的时空充电负荷模型综合考虑了人们的出行特征、充电地域差异及充电习惯对电网调度的影响。缺陷在于，本文仅考虑以最优填谷为目标的充电方案，未考虑充电经济性因素。电网实时电价的变化对充电总成本会产生较大的影响，在实际充电优化中需要考虑。