多个海上风电场输电组网拓扑研究

王长虹，刘天琪，李保宏

(四川大学电气信息学院,四川成都 610005)

0 引 言

海上风电具有资源丰富、发电利用小时数高、不占用土地、不消耗水资源和适宜大规模开发的特点。近年来，海上风电开发已经成为全球新能源开发的热点与前沿，目前世界上最大的海上风力发电厂为英国的“伦敦阵列项目”，预计总装机容量1 000MW，离岸约20km，分别设两个海上升压站，两个海上升压站通过4个150kV接地电缆被连接到克利夫山的升压站，并在此并入现有的400 kV电网[1-3]。

目前，国内海上输电一般是各风电场分散并网，不利于海上输电网的整体运行和调度，而多个海上风电场输电组网的研究能够实现海上风电场与大陆电网的协调对接。随着海上风电场数量不断增加，依据相关规程通过人工设计海上风电场输电网接线方案费时费力，且可能因考虑不周遗漏更为合理的方案。因此，对多个海上风电场构建的输电网拓扑自动生成算法的研究显得极为重要。

虽然陆上区域电力网规划设计已有成熟的设计规程规范，有些运用遗传算法结合最小路径法完成规划，也有一些文献对海上风电接入陆地系统方案进行研究，如文献[4]研究了多个近海风电场接入陆地升压站的方案，文献[5]指出德国海上风电并网方案的改变，由原来的各风电场分散并网转变为以风电场群为单位的集中并网模式，介绍了几种基于人工设计的风电场群接入方案，文献[6-7]研究了单个风电场集电系统内部的拓扑连接方式及优化方法，提出了基于遗传算法，prim最小生成树法及多元旅行商算法的拓扑优化方法。

但是，对海上风电场输电网和拓扑设计的研究不多，且大多基于人工设计，未考虑计算机自动生成方案，也没有考虑多个风电场输电网的拓扑；而且风电场集电系统的拓扑优化只是针对位置固定的风机间单条连线电缆不同截面的优化，没有考虑多风电场组网输电网多条出线的问题。

为此，本文以某地区海上区域风电场为例，重点研究在升压站和集控中心位置不确定，且升压站多条出线的情况下自动生成多风电场输电组网最优拓扑方案的方法。首先运用DFS(深度优先搜索法)和最短路径法形成初始方案，然后通过基于Dijkstra(迪杰斯特拉)算法的改进遗传算法获得输电组网经济性最优的拓扑结构，以及升压站和集控中心的最佳位置，并通过算例验证了该算法的有效性和应用范围。

1 海上输电组网投资成本的数学模型

1.1 海上输电组网投资成本

海上输电组网优化的主要内容是根据升压站和陆上集控中心的位置信息(各升压站和集控中心分别位于固定的7个区域)优选接线方案和最佳位置，典型的海上输电组网方案如图1所示。

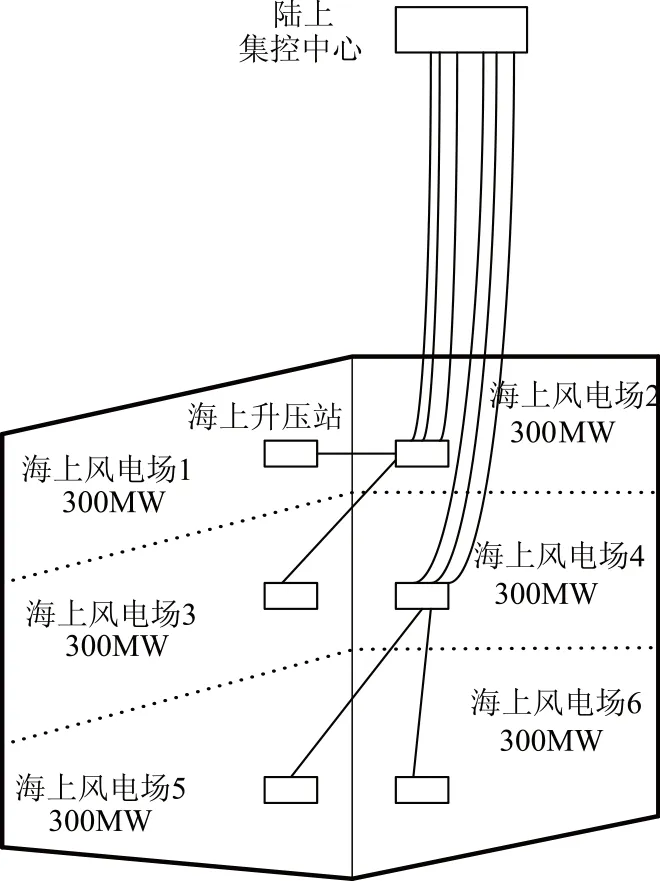
图1 海上输电网连接拓扑示例Fig.1 Example of offshore grid connection topology

海上风电场输电系统的总投资成本Ecost主要包括3部分，设备投资成本Cf、维护成本Cm和损耗费用Closs[8]。

① 设备投资成本

Cf=C1+C2+C3

(1)

式中：C1为升压站投资成本，主要包括变压器高、低压仓位、所选变压器的成本，无功补偿电容器和开关设备的投资成本，以及升压站的建设成本[9]。C2为电缆投资成本，C3为无功功率补偿成本。

C2=(P1+P2)l

(2)

式中：P1为电缆单位长度价格;P2为电缆单位长度敷设成本;l为电缆的长度。

② 维护成本Cm

如果输电系统生命周期内维护成本占总投资成本百分比P为已知数据，则交流输电系统年维护成本占总投资成本百分比为A：

(3)

式中：i为年利率；n为生命周期。

Cm=A×Ecost

(4)

③ 损耗费用Closs

Closs=Csub+Cline

(5)

式中：Csub为升压站损耗费用;Cline为线路损耗费用。

1.2 简化数学模型

为了突出输电组网经济性，本文不考虑系统稳定性、继电保护以及潮流分布问题且假设海底电缆可自由敷设[10]。

通过调研知[11-14]，在不同输送距离条件下，交流输电电缆和升压站两部分成本之和占总成本的96.80%，同时考虑到升压站设备投资成本主要与风电场容量相关，输电网拓扑的变化不会对升压站初始设备投资产生影响，维护成本的百分比已知，因此，在拓扑设计中仅需考虑电缆部分投资即可反应经济性。

因此，本文在进行输电组网拓扑优化时，以输电组网所需海底电缆总长度最小为优化目标，即目标函数为

min(Lsum)

s.t.Sbranch≤Smax

Oi⊂Zii=1,2…7

(6)

式中：Lsum为海底电缆的总长度;Sbranch为输电组网中每一条海底电缆上传输的视在功率；Smax为每条海底电缆所能传输的最大视在功率；Oi为升压站或集控中心的位置；Zi为给定的升压站或集控中心所在的区域。

同时，考虑到输电网拓扑的变化会影响其可靠性，设定最低可靠性要求作为限制条件。优化设计时，采取以经济性成本为目标选取多个满足可靠性限制条件的经济最优及次优的方案，然后对其进行详细的可靠性分析，最后通过权重法选取工程需要的最优拓扑方案。

2 基于 Dijkstra(迪杰斯特拉)改进遗传算法的拓扑设计

由于海上输电组网的拓扑总方案数量可观，为使算法层次分明，并加快算法的运行速度，本文分两层进行优化：首先，运用DFS(深度优先搜索法)和最短路径法形成初始可行方案，然后通过基于Dijkstra(迪杰斯特拉)算法的改进遗传算法获取最优方案。

以海上风电场输电组网消耗的海底电缆总长度的倒数作为算法的适应度函数，按下式计算适应值：

F=Lsum

(7)

显然，总长度越小，适应值越小，个体越符合要求。

2.1 初始可行方案的形成

2.1.1 升压站和集控中心位置选取

由于升压站和集控中心位置不确定，分别位于7个给定的区域，遍历区域中的所有点工作量太大，本文采取在每个给定的区域内随机取一个初始点，然后在该点周围等间隔取3个点，验证算法结果与理论是否相符。

2.1.2 拓扑方案编码

图2 基因编码Fig.2 Coding of chromosomes

2.1.3 形成初始优质种群

编码完成以后，产生初始种群，由于初始种群庞大且有很多不可行解(拓扑图不连通或者不是最小连通拓扑图)，DFS(深度优先搜索法)可判断图的连通性，而最短路径法可筛选出同一个起点和终点的最短路径；因此，本文结合DFS(深度优先搜索法)和最短路径法得出连通且路径最短的初始优质种群，即为初始可行方案。

2.2 拓扑方案的优选

2.2.1 基于Dijkstra(迪杰斯特拉)的多条出线适应度求解

考虑到单个风电场的容量较大(按目前的建设规模，可以假定为每个300MW)，而送出电缆的截面不能无限放大，因此，如果第一级送出电缆为220kV，3根单芯，截面为1 000mm2，第二级电缆只能取2回路3×1×1 000mm2。第三级则为三回，以此类推。

如此，单纯依靠普通的旅行商算法[15]与Prim最小生成树算法[16]求距离和是不能满足要求的。而 Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止，有一个确定的起点(源点)，其余为终点，源点到各终点两顶点的路径最短[17]。该方法可有效解决多回出线的问题。Dijkstra(迪杰斯特拉)算法求总路径的过程如图3所示。

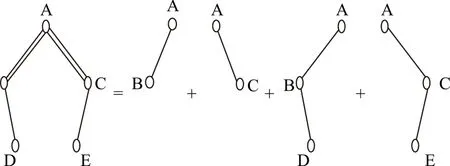
图3 Dijkstra求总路径过程示意Fig.3 Example of seeking total path

2.2.2 改进的遗传算法

由于个体数量庞大，全部遍历耗时长，本文对标准遗传算法进行如下改进：

① 先选取200个个体进行标准遗传算法，得出1个最优解；

② 将该最优解与下一个含有199个个体的种群组合，继续进行标准遗传算法；

③ 如此迭代10次，在第10次得到最优拓扑连接方式(即放射形)时，在该最优连接方式的基础上重新遍历每一个区域的所有点，以免遗漏最优个体。

经过上述改进遗传算法的筛选，最终可获取最优拓扑方案。

2.3 算法流程

本文设计的基于Dijkstra(迪杰斯特拉)并结合DFS(深度优先搜索法)的改进遗传算法流程如图4所示。

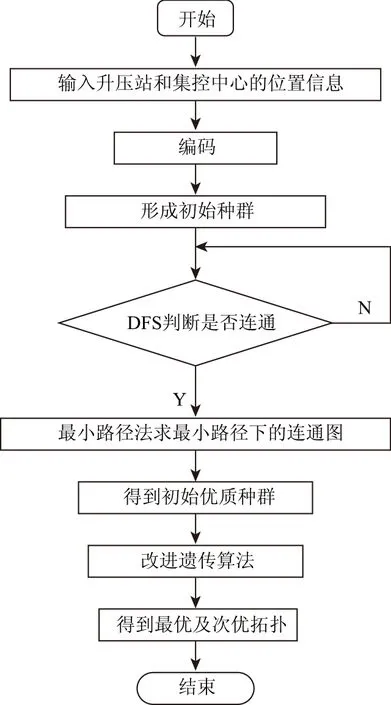
图4 算法流程图Fig.4 Flowchart of the algorithm

3 算例分析

为验证所提算法的有效性，对广东某区域6个容量为300MW的海上风电场输电组网的网络拓扑进优化。对升压站和集控中心位置确定和不确定两种情况进行分析。

优化过程中使用的GA参数如表1所示。

表1 遗传算法系数

升压站和集控中心位置确定时,读取升压站和集控中心的位置信息，运用该算法可快速生成优化拓扑连接方式。初始随机拓扑和满足可靠性要求的经济性最优及次优拓扑如图5所示。

图5 固定升压站和集控中心位置的拓扑优化示意Fig.5 Example of the topology’s optimization of fixed stations of the boosters and centralized control center

升压站和集控中心位置不定时,各升压站和陆上集控中心选址不定，以经济性最优为目标，电缆总长度为目标函数，运用本文算法自动生成初始随机拓扑和满足可靠性要求的经济性最优及次优拓扑如图6所示。

该算法在这两种情况下得到的最优及次优基拓扑如图5(c)和图6(c)所示。两种情况下最优和次优拓扑编码及适应度结果如表2所示，图5、6中1代表陆上集控中心，2-7代表海上升压站，实心圆代表初始点，空心圆代表等间隔所取点。

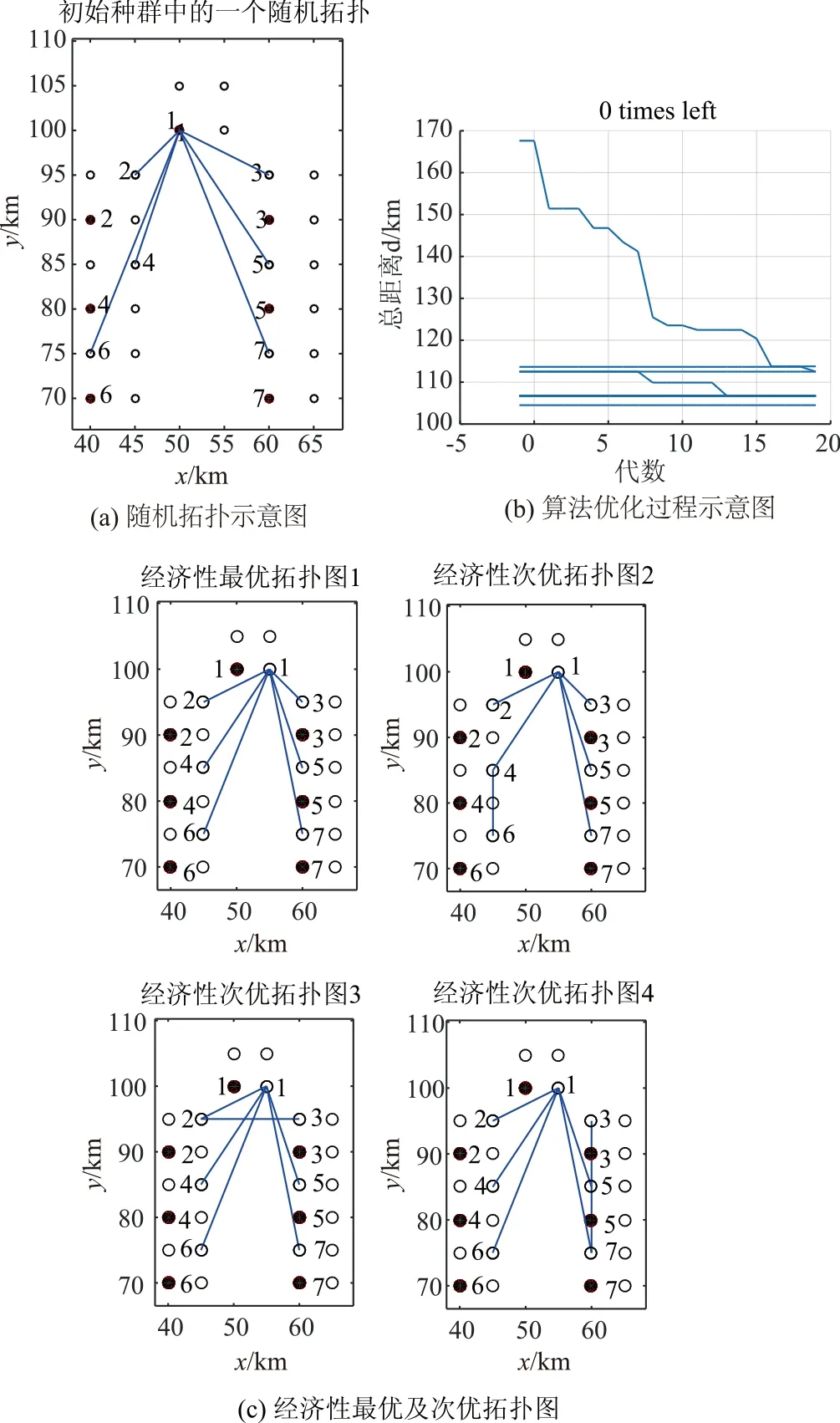
图6 升压站和集控中心位置不定的拓扑优化示意Fig.6 Example of the topology’s optimization of unfixed stations of the boosters and centralized control center

由图5、 6及表2可得：

① 在升压站和集控中心位置固定和不固定两种情况下经过算法优化仿真得出的结论相似，即放射形组网拓扑所用海缆长度最短，总消耗费用最少，为经济性最优的组网拓扑结构，次优组网方案所需费用略小于最优拓扑。

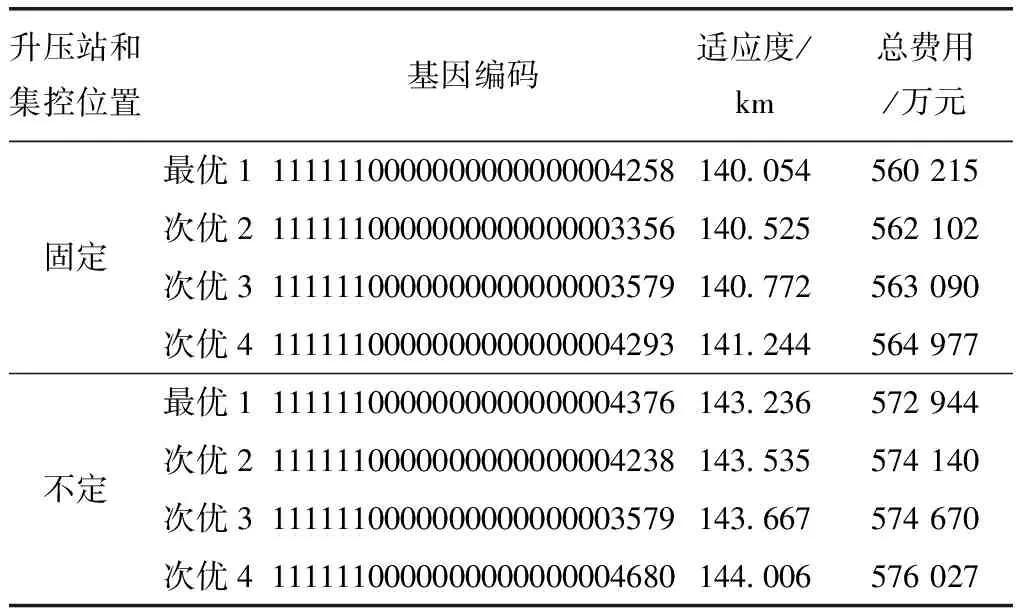
表2 两种情况下最优和次优拓扑编码及适应度结果

② 由图5(b)、6(a)可知，DFS(深度优先搜索法)和最短路径法能够保证仿真所得拓扑路径最短且具有连通性，图6(b)可以看出，基于Dijkstra(迪杰斯特拉)并结合DFS(深度优先搜索法)的改进遗传算法具有收敛快，结果精准的优点。

③ 由图6(a)、(c)可知，该算法可在升压站和集控中心位置不定的情况下精确地选出最优位置的拓扑连接方式。

筛选出数量有限的满足可靠性限制条件的经济性最优及次优拓扑结构后，运用蒙特卡洛法[18]或最小割集法[19]对其进行详细的可靠性分析，最后，通过权重分析法选取满足实际工程需要的经济性和可靠性均最优的拓扑方案。

4 结束语

本文解决了海上输电组网的拓扑设计问题，考虑到升压站和集控中心位置不确定且升压站有多回出线，设计出一种基于Dijkstra(迪杰斯特拉)并结合DFS(深度优先搜索法)的改进遗传算法，该算法克服了普通遗传算法的早熟及运行时间长的问题，能有效找到输电组网的最优方案。算例证明该算法的有效性和最优拓扑方案的可行性。此外，该算法也可对每个区域形状进行改变，并且可规避不能敷设电缆的坐标区域，灵活性强，能运用到其他海域海上风电场输电组网的拓扑设计，具有很大的扩展性。