基于Workbench差速器齿轮的疲劳分析
,, ,,贺贺
(江苏科技大学机械工程学院,江苏 镇江 212003)
0 引言
差速器作为汽车传动系统的重要部分,而差速器齿轮又是差速器中主要零件,因此其可靠性直接影响汽车整车的质量。差速器齿轮一般在恶劣的工作环境下运行,并且汽车的行驶速度也是在不断变化,从而使其档位多变。如果齿轮受到过大的接触应力或者应力分布不均匀,都会使齿轮产生破坏,如齿面点蚀、塑性变形等。将会导致齿轮传动失效,从而影响到汽车差速器的各种性能参数。因此,对差速器齿轮的有限元分析、动态啮合仿真分析以及疲劳性能分析具有重要意义。
使用CATIA软件建立齿轮的几何模型,然后导入有限元软件Workbench中进行分析[1]。齿轮的应力最大位置即有可能发生疲劳失效的位置,利用ANSYS Workbench Fatigue Tool疲劳分析工具对差速器齿轮进行疲劳寿命仿真,获取相关的疲劳寿命仿真结果。
1 典型工况下转速和转矩的计算
汽车在行驶过程中,差速器将会经历不同的工况条件,这主要是由于差速器的工作原理导致。汽车行驶时,驱动力来自于驱动桥总成,经过主减速器和差速器壳传送到一字轴处,最终通过差速器中2个行星齿轮传递到汽车两端驱动车轮[2]。差速器如图1所示。

图1 差速器示意
对于在不同工况下,计算齿轮所受到载荷的大小,为了能得到准确结果,所有工况的计算均在差速器到达最大转矩下进行。通过查阅相关资料,当变速器处于最低挡并且发动机输出最大转矩时,差速器壳将会获得最大转矩,同时齿轮转矩也会达到最大值。差速器受到的转矩为[2]:
(1)
式(1)的相关参数如表1所示。

表1 汽车相关参数
由图1可得,差速器中壳体与齿轮的转矩关系为:
(2)
T1,T2分别为左右两半轴对差速器的反转矩;Tr为差速器的内摩擦力矩;k为差速器锁紧系数,一般取值0.05~0.15,这里取0.1。
结合式(1)、式(2)以及表1计算,可得半轴对差速器较大的反转矩T2=1 837 N·m,结果除以行星齿轮数2,即可得到单个半轴齿轮对单个行星齿轮的转矩约为919 N·m。
差速器半轴齿轮、行星齿轮的转速关系为:
(3)
ω0为差速器壳角速度即行星齿轮公转角速度;ω1,ω2分布为两侧半轴齿轮自转角速度;ω3为行星齿轮的自转角速度;rp为行星齿轮节圆半径,此处为53 mm;rs为半轴齿轮节圆半径,此处为74.2 mm。
汽车在低速挡,稳定高速行驶时,发动机转速在2 500 r/min左右,根据表1中的变速器最低挡变速比和主减速器传动比,可以计算出差速器壳最大角速度ω0=18 rad/s。汽车在行驶中,差速器主要有2个典型工况:当汽车保持直线行驶时,行星齿轮不发生自转,只跟随差速器壳的转动而转动,此时行星齿轮、半轴齿轮的角速度与差速器壳的角速度相同;当汽车发生转速行驶时,行星齿轮不仅只跟随差速器壳的转动而转动,而且还发生自转运动,左、右半轴的转速将会不相等,一般情况下,转速相差100 rad/s,从而实现差速,结合式(3)可计算出,此时行星齿轮的自转角速度ω3=8 rad/s。
2 有限元模型的建立
基于Workbench有限元分析软件,通过CATIA绘制的差速器三维模型导入Workbench中进行网格划分,赋予材料属性、设定边界条件、施加转矩及转速,对差速器总成进行运动学分析以及疲劳寿命分析。
2.1 网格划分
Workbench具有强大的网格划分功能,一般在进行网格划分前,往往需要对几何模型实施简化处理,达到提高计算效率的目的[3]。针对本课题差速器齿轮的结构,综合分析后进行了如下简化:忽略半轴齿轮和行星齿轮上的油孔;忽略半轴齿轮轴孔内的花键[4]。齿轮网格划分采用正六面体单元进行划分,半轴齿轮网格尺寸为0.8 mm,行星齿轮网格尺寸为1 mm,结果如图2所示。划分为642 779个节点,191 441个单元。

图2 齿轮网格划分
2.2 材料属性
差速器行星齿轮和半轴齿轮的材料均采用20CrMnTi,材料密度为7 870 kg/m3,弹性模量为208 GPa,泊松比为0.295。
2.3 边界条件及载荷施加
对齿轮的接触问题,边界条件的施加尽可能与实际情况相吻合[5]。差速器在低挡情况下,行星齿轮受到发动机输入的转矩作用,以相应的转速转动,带动半轴齿轮转动。行星齿轮为主动轮,半轴齿轮为从动轮。两齿轮间通过相互间的接触作用传递扭矩。在齿轮传动过程中,齿面接触瞬间,行星齿轮还没有受到半轴齿轮的带动作用,所以是固定不动的,应全约束,但需要保留行星齿轮的旋转自由度。
通过上述分析,在Workbench软件中进行约束的添加,通过Fixed Support将半轴齿轮中心圆柱面固定,限制其各个方面的平动和转动;然后利用Cylindrical Support在行星齿轮中心圆柱面添加上圆柱面约束,约束其径向和轴向的运动;使用Moment在行星齿轮中心圆柱面上施加转矩载荷919 N·m;当处于汽车直线行驶工况时,直接对行星齿轮施加绕Z轴转动的角速度为18 rad/s,当处于转弯工况时,对行星齿轮施加绕其轴线转动的角速度为8 rad/s。
3 运动仿真分析
运行瞬态动力学分析差速器齿轮,能够很好地得出在不同工况载荷下的响应。Workbench对运动学仿真也具有普遍的应用[6]。针对本课题差速器齿轮的运动仿真,主要从保持直行工况和转弯工况这2种典型工况进行分析。
3.1 直行工况下的应力分布
汽车在保持直线行驶时,行星齿轮只随着差速器壳体的转动而转动,并不发生自转运动。应力主要分布在齿轮啮合面处,达到最大值是在齿轮转矩到最大值以及转速到达此刻最大的转速的状态下。为了方便观看应力分布情况,此处分别选取行星齿轮与半轴齿轮的单齿进行分析,如图3所示。由图3可知,最大应力都发生在齿轮小端啮合处,行星齿轮的最大接触应力为1 201 MPa,半轴齿轮最大接触应力为1 438 MPa。

图3 直行工况下单齿应力云图
3.2 转弯工况下的应力分布
汽车在转弯时,此时差速器进行差速运转,行星齿轮不仅跟随差速器壳的转动而转动,而且行星齿轮自身发生自转。但是当应力达到最大时的状态和直行行驶工况下的状态一致,都是转矩达到最大值以及转速达到此刻的最大值。同样选取单个齿轮进行分析,如图4所示。由图4可知,最大应力都发生在两齿轮啮合时齿顶所触及的齿根位置,行星齿轮的最大接触应力为1 232 MPa,半轴齿轮最大接触应力为1 645 MPa。
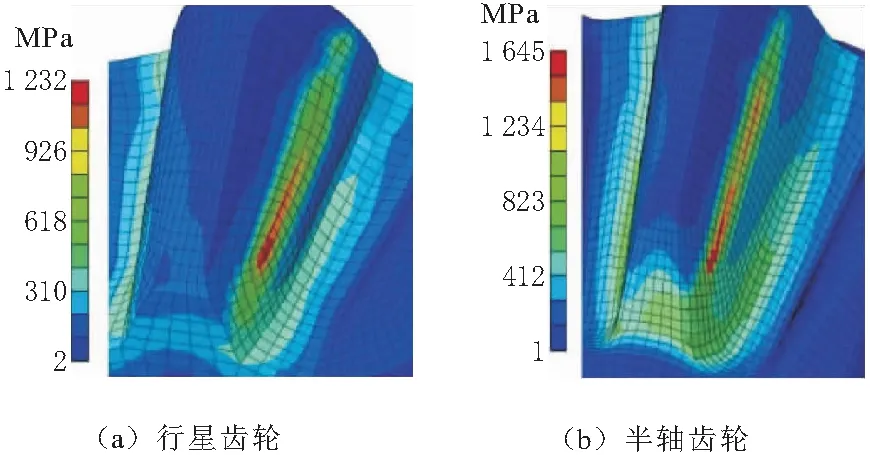
图4 转弯工况下单齿应力云图
综上分析可得,差速器齿轮处于2种典型工况下,最大应力为接触应力,发生在转弯工况下,最大值为1 645 MPa,由于齿轮均为锥齿轮,其成型工艺为近净成型,接触面经过后处理加工,其接触疲劳强度极大值一般为2 250 MPa。因此,本次计算结果小于其极值,满足应力要求。
4 疲劳分析
差速器齿轮所受到的转矩是反复作用的,即使所受到的转矩较小,但是经过多次反复的转动,齿轮也会出现断裂现象。对于这种转动齿轮的疲劳破坏是最常见的破坏现象。所以,为了避免齿轮在运转中发生断裂,影响工作,此处将对齿轮进行疲劳分析,从而预测齿轮在发生疲劳破坏时的最大使用寿命。借助上文对齿轮的运动分析,确定齿轮最大应力以及产生最大应力的位置。当齿轮处于最大应力时,对单个齿轮进行疲劳强度分析。
4.1 疲劳载荷的设计
差速器齿轮材料为20CrMnTi,通过查阅文献以及相关手册可获得,当疲劳分析曲线的存活率为90%的状况下,其循环次数与应力强度曲线如图5所示。通过对齿轮的运动仿真分析,利用齿轮受到最大应力的位置即齿根处进行疲劳分析,采用正弦载荷作为齿轮所受到的疲劳载荷,正弦载荷从最大值1到最小值0,此值是相对于实际载荷的一个比例系数,即当正弦载荷处于1时,实际载荷为最大载荷值。齿轮在转动时,单个齿所受到的转矩通过最大值1转到最小值0,反复运动,其运动周期为0.31 s。正弦循环载荷谱如图6所示。
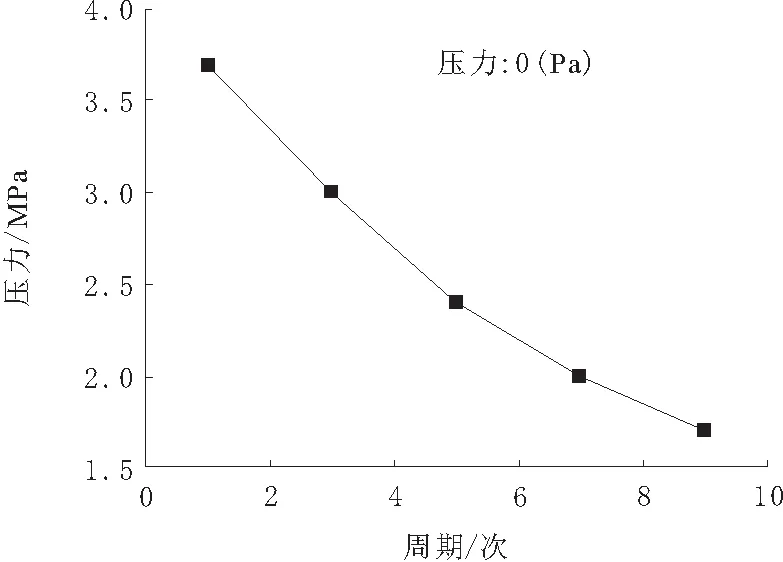
图5 材料20CrMnTi的S-N曲线
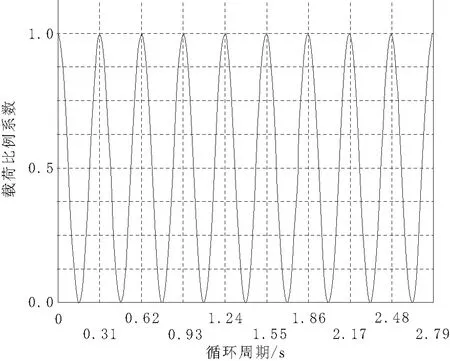
图6 循环载荷谱
4.2 疲劳分析结果
当齿轮在循环载荷作用下,齿轮根部容易发生疲劳失效。由于Workbench Fatigue Tool疲劳分析功能只能简单计算出指定位置循环次数下的疲劳耗时系数。所以,利用齿轮单齿的齿根接触应力结果以及相应的疲劳载荷和材料S-N曲线相结合,计算出齿轮的疲劳寿命[7-8]。
通过Workbench进行齿轮疲劳寿命的计算分析,分别得出单齿行星齿轮以及单齿半轴齿轮的疲劳寿命云图如图7和图8所示。通过对图7进行分析,得出行星齿轮齿根部位不仅是所受应力最大的位置,也是所受寿命最低的区域,即最容易发生齿轮断裂的位置。行星齿轮最低寿命为4.96×105次循环,在不超过这个循环次数时,行星齿轮处于相对安全状态。
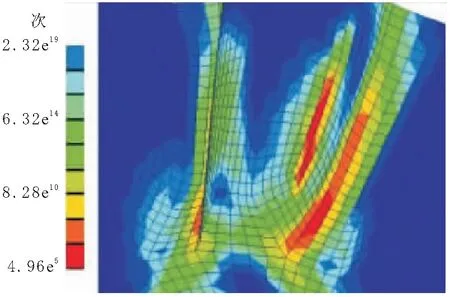
图7 行星齿轮单齿疲劳寿命云图
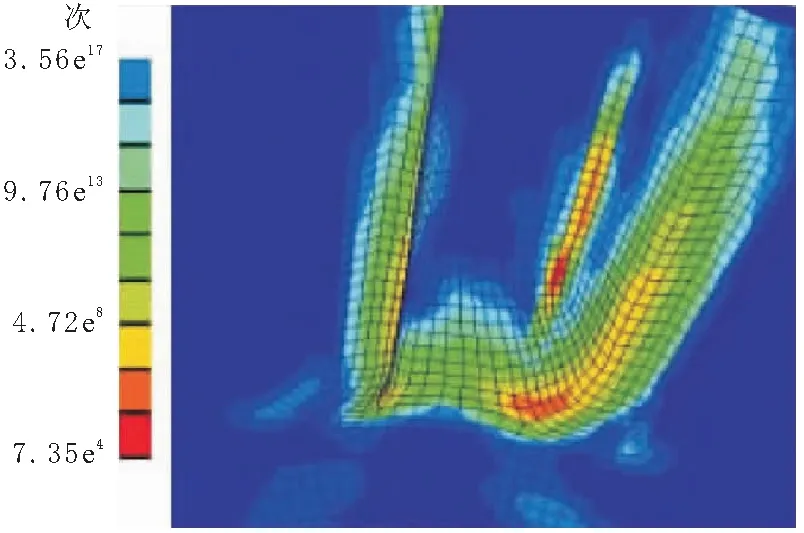
图8 半轴齿轮单齿疲劳寿命云图
对图8进行分析可知,半轴齿轮的最低疲劳寿命区域仍发生在应力最大的位置,对于半轴齿轮来讲,应力最大的位置在小齿根处,通过与行星齿轮对比,得出疲劳寿命最低的区域一般发生在应力最大的位置。半轴齿轮最低寿命为7.35×104次循环,当超过这个循环次数时,半轴齿轮有可能发生断裂。
由于差速器处于不同工况下运行,当处于直线行驶的工况时,行星齿轮并不做自转运动,此时不起差速作用。
只有当汽车进行转弯行驶时,差速器齿轮处于转弯工况下,行星齿轮发生自转运动,将会使2个半轴齿轮的转速发生不同步现象,此时差速器才起到差速作用。由于差速器齿轮并不是一直保持工作状态,因此,本设计差速器齿轮的疲劳寿命满足要求。
5 结束语
通过三维绘图软件CATIA对差速器齿轮进行几何建模,并且结合有限元软件Workbench进行仿真分析,得出了在不同工况下行星齿轮与半轴齿轮的最大接触应力,以及最大应力所产生的位置,验证了此设计齿轮满足应力要求。借助仿真分析结果以及材料的S-N曲线,利用Workbench Fatigue Tool进行齿轮的疲劳寿命分析,发现疲劳寿命最低一般发生在所受应力最大的位置,同时分别得出了行星齿轮与半轴齿轮的最低寿命循环次数以及当超过最低循环次数时,齿轮最可能发生破坏的位置。
——对2018年广州市一道中考题的研究

