精选基本图形，研发“一图一课”——以“对角互补四边形”微专题复习课为例

☉江苏省海安市城南实验中学 顾志勇

中考微专题复习是近年来的一个教研亮点，我们在《中学数学（初中版）》就曾见到多篇研究微专题的课例，深受启发，笔者在教学实践中围绕“对角互补四边形”也研发了一节习题课，本文梳理出来，分享给大家.

一、“对角互补四边形”专题复习教学流程

教学环节（一） 基础热身

例1 如图1，在△ABC中，D是BC边的中点，DE⊥BC交∠BAC的平分线于点E.连接BE、CE.

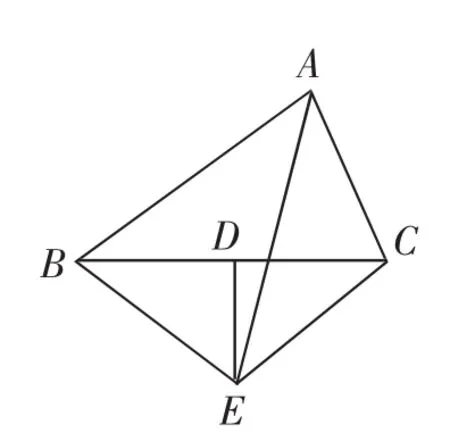
图1

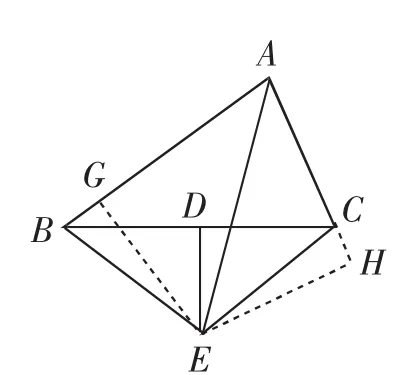
图2

（1）点E到B、C两个端点距离相等吗？说说你的依据.

（2）点E到AB、AC的距离相等吗？说说你的依据.

（3）若∠BAC=80°，求∠BEC的度数.

（4）小可发现∠BAC+∠BEC是一个定值.你觉得小可的发现正确吗？

教学组织：前两问是让学生复习两个定理，线段垂直平分线上的点到线段两端点距离相等；角平分线上的点到角的两边距离相等.第（3）问需要作辅助线，如图2，过点E向AB、AC作垂线段EG、EH，可利用“HL”证Rt△BGE Rt△CHE，得∠BEG=∠CEH，再把目光转向四边形AGEH中，可得∠GAH+∠GEH=180°，于是结合∠BEG=∠CEH，转化为∠BEC+∠BAC=180°.教学过程中先安排学生独立探究，再在小组内交流思路，并由学生代表汇报展示，教师根据学生的讲解追问思路，对于关键步骤可以让其他学生复述.

教学环节（二） 拾级而上

例2如图3，在Rt△ABC中，O是斜边AB的中点，DO⊥AB交∠BCA的平分线于点D，DE⊥AC于点E，DF⊥BC于点F.

（1）求证：△ADE △BDF.

（2）小天发现∠DAC+∠DBC是一个定值.请判断小天的发现是否正确.

（3）设AC=6，BC=2，求四边形ADBC的面积.

（4）在（3）的条件下，求CD的长.

教学组织：前两问是例1的变式再练，安排学生复述思路即可.第（3）问需要借助前两问的进展，得出AE=BF，再得出CE=CF，AC-AE=BC+BF，于是CE=CF=4，再证四边形CEDF为正方形，它的面积为16，再结合△ADE △BDF，四边形ADBC的面积可转化为正方形CEDF的面积16.相应的，发现△CDE是等腰直角三角形，有CD=4.

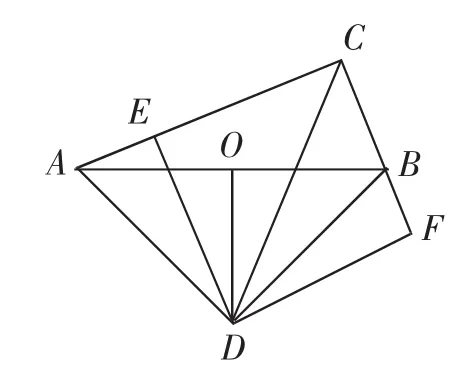
图3

图4

教学环节（三） 圆的视角

例3如图4，AB为⊙O的直径，点C、D在圆上，连接AC、BC，CD平分∠ACB，连接AD、BD.

（1）判断△ABD的形状，并说明理由.

（2）若⊙O的半径为5，求AD的长.

（3）在（2）的条件下，BC=6，求CD的长.

（4）小婧经过探究，发现不需要（2）中的条件，也可证出AC+BC=CD.你觉得得小婧的探究是否正确？说说你的分析.

教学组织：对于第（1）问，除了可以转化为例1、例2中的思路处理，还可以结合圆周角性质（根据同弧所对圆周角相等，∠DAB=∠DCB，∠DBA=∠DCA），快速实现问题突破.对于第（2）问，可延续上一问的进展，利用等腰直角三角形的性质，直径即斜边AB=10，可得AD=BD=5对于第（3）问，利用之前例2中的一些进展，构造图5，突破△CDE为等腰直角三角形，求出BF=AE=1，于是CE=7，即CD=7.当然解法并不唯一，学生也可“旋转”△BCD到△AGD的位置，构造图6中的△CDG，证出等腰直角三角形，也可实现问题解决.第（4）问则是“走向一般”，利用上一问中两种构图都可解决问题.比如图5中，先证出AC+BC=2CE，而CD=CE，即AC+BC=CD.另外，利用图6中的进展，把目光投向等腰直角三角形CDG，也可得出CG=CD，即AC+BC=CD.

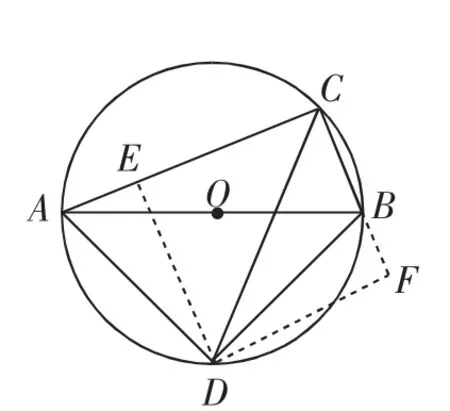
图5

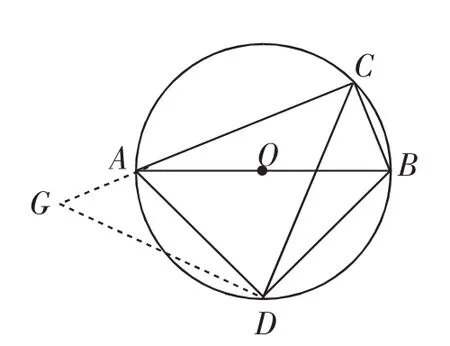
图6

教学环节（四） 变式拓展

例4如图7，AB是⊙O的直径，AC是⊙O的弦，∠ACB的平分线CD分别交⊙O于D，交AB于M，连接AD、BD.

（1）请你过点D分别向AC、BC作垂线段，垂足分别为点E、F，求证：四边形CEDF为正方形.

（2）直接写出AC、BC、CD之间的数量关系.

（3）设DA=m，DC=n，试用含m、n的代数式表示△ABC的周长.

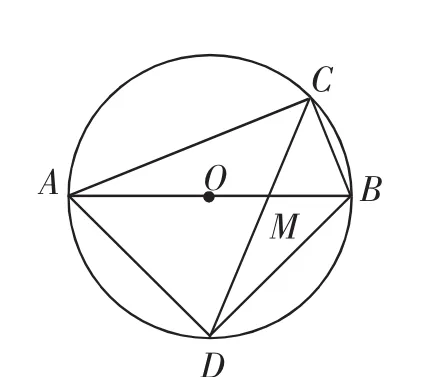
图7

教学组织：前两问是例3的简单变式.对于第（3）问，可利用例3（4）获得的结构与性质，构造出图5或图6，是△ABC的周长为对于第（4）问，由△ACM △DBM，可得，由△BCM △DAM，

二、教学立意的进一步解读

1.精心选取基本图形，研发“一图一课”

本课我们选取的是“对角互补四边形”这一基本图形，该图形融角平分线、垂直平分线于一题之中，既需要角平分线的性质定理、线段垂直平分线的性质定理证线段相等，又需要借助全等来“导角”，对证明过程中“导边”“导角”的基本功有较好的训练.从这个基本图形出发，通过例1让学生经过热身训练，过渡到例2拾级而上，再到例3结合圆的视角看清问题的结构，最后的例4仍然以圆为背景，变式再练、拓展提升，起到了较好的教学效果.

2.贯通不同年级章节，践行“开放教学”

上面的4个例题中，例1、例2分别对应着八年级上学期全等三角形、等腰三角形的学习，例3对应着九年级上学期圆的学习，例4对应着九年级下学期相似三角形的内容，4个例题源于一个基本图形，环环相扣，贯通了不同年级和章节，作为中考专题复习，打破年级、章节的界限，借助一个图形综合不同的知识点，让研究问题的视角打开，使学生学会根据问题条件或信息解读、调取不同章节的数学内容，辅助解题，践行了所谓“开放式教学”（郑毓信教授语）的追求.

3.遵循深入浅出原则，预设“铺垫问题”

在具体构思“一图一课”时，既要注意循序渐进，由浅及深，又要注意在呈现一些拓展问题之前，增设一些铺垫式问题，让学生循着铺垫问题自主获取思路，既学会解题，又能收获解题自信.比如根据教学经验，例3的第（4）问是很多学生不太适应的一种问题，因为在圆的背景中，学生往往思路局限在圆的“内部”（不只是指圆这个图形内部，学生的眼光也局限于利用圆这一章中的知识点解题），不能跳出圆的视角联想到八年级“旋转”构造全等、证明特殊直角三角形来实现问题的贯通.这样，我们有了例2的几个设问的铺垫，当学生没有进展时，可以启发他们“回看”例2，容易获得有效的构造与转化，实现问题解决.