贴近目标精选例、习题，训练眼力聚焦判别式——“一元二次方程根的判别式”同课异构研讨

☉江苏省太仓市实验中学 朱 鸣

一元二次方程根的判别式是一个十分重要的知识点，不只是在一元二次方程中有较多的应用，将来研究二次函数图像与x轴或另一直线的交点时仍然显现出“以数驭形”的威力.在新授课上，需要安排一课时进行教学，而不只是像有些教材一样只是在讲求根公式时“一带而过”，待以后习题课时再专门分类训练.文［1］提出“用教材教”，并给出一元二次方程根的判别式的教学设计，笔者以该教学设计为基本框架，在自己班级进行教学，取得了较好的教学效果.本文给出该课教学流程与具体的实施方法，并跟进教学立意的阐释，作为一种读刊后的同课异构教学实践，供研讨.

一、教学流程

说明：本课是在学生刚学过配方法、用求根公式法解一元二次方程之后安排的一节新授课，主题学习一元二次方程根的判别式.

活动（一） 从一元二次方程的解法引入新知

用恰当的方法解下列方程：

（1）x2+2x-1=0；（2）x2-2x+1=0；（3）x2+2x+2=0.

教学实施：学生利用配方法或求根公式法分别解两个方程后，发现第（3）题没有实数根；求解之后，安排学生走向一般，说说一元二次方程ax2+bx+c=0（a≠0）的根的情况可以怎样快速判定.

教学预设：将配方后得到的方程书写到黑板上，如下：

学生应该能把目光锁定在一个关键的表达式“b2-4ac”上，因为上面提供的3个方程恰恰对应着不同的解的情况，在学生小结的基础上形成板书（写到右侧“副板区”，略）.

活动（二） 聚焦关键代数式，研究根的判别式

定义：把b2-4ac叫作一元二次方程ax2+bx+c=0（a≠0）的根的判别式，记作Δ=b2-4ac.（完善板书，对应着上面“副板区”的内容，书写在左侧的主板区）

对于一元二次方程ax2+bx+c=0（a≠0）：

Δ＞0⇔方程有两个不相等的实数根；

Δ=0⇔方程有两个相等的实数根；

Δ＜0⇔方程没有实数根.

教学实施：上述“判断”正、反过来理解，都是正确的.教师先正、反分别讲解一遍，然后请三个不同的学生各复述一次（重要内容适当重复几遍）.

活动（三） 精选典型例题，运用新知解决问题

例1不解方程，判断方程3x2+2=3x根的情况.

教学实施：要求是不解方程，但是学生展示解答时需要有“化为一般式”的过程，这是明确“a、b、c”的关键一步，在此基础上计算“根的判别式b2-4ac”进行判定.

跟进练习：判断以下方程根的情况（不解方程）：

（1）3x2+4x=-5；（2）2x（x-3）+4=0；（3）3x2-5x-21=0.

教学实施：前两问主要是训练学生将方程化为一般式再计算、判定，第（3）问可直接计算判断根的情况，但是可增加一个追问：有没有更快速的判定方法？如果学生不能发现，可以提示：有人认为只要二次项系数、常数项异号就一定能判定方程有两个不相等的实数根！大家认可这一判断吗？引导学生认真观察“根的判别式b2-4ac”，将其拆分为b2、-4ac后，就能确认上述判断了.

活动（四） 含参问题训练及变式，巩固新知

例2不解方程，小强认为可以判断关于x的方程x2-mx-m2=0（其中m是实数）一定有两个实数根.你觉得小强的判断是否正确？说说你的理解.

教学实施：根的判别式b2-4ac=5m2≥0，即方程有两个实数根（注意可能是两个相等的实数根，也可能是两个不相等的实数根），所以小强的判断是正确的.

例3若a为实数，有两个方程：关于x的方程x2+3xa+2=0 ①；关于y的方程ay2+2（a+1）y+a-1=0 ②.

（1）当方程①有实数根，且方程②为一元二次方程时，试判断方程②解的情况；

（2）当方程①有实数根时，直接写出方程②解的情况.

教学实施：（1）方程①一定是一元二次方程，可先计算“根的判别式b2-4ac”得出4a≥-1，再计算出后一个关于y的方程②的“根的判别式b2-4ac”为12a+4，于是可确认12a+4＞0，即关于y的一元二次方程有两个不相等的实数根.

（2）与（1）相比，变化在于将“一元二次方程”变式为“方程”，学生需要看清辨明，考虑关于y的方程中a=0的情况.

活动（五） 课堂小结与目标检测

（1）方程5x2=-2x没有实数根.（）

（2）如果一元二次方程ax2+bx+c=0有两个实数根，那么Δ＞0.（）

（3）如果a、c异号，那么方程ax2+bx+c=0有两个不相等的实数根.（）

2.不解方程，判别下列方程根的情况：

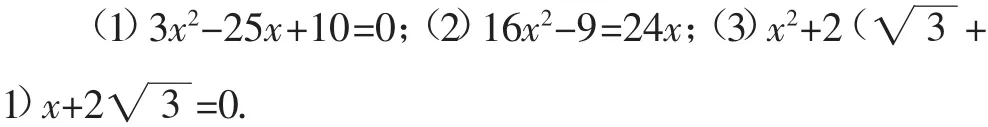
3.已知关于x的方程x2+2x-a+1=0没有实数根，试判断关于x的方程x2+ax+a=1是否一定有两个不相等的实数根，并说明理由.

选题立意：这组检测题在于检测学生是否理解根的判别式的意义，能否用根的判别式判断一元二次方程根的情况，以及书写是否规范.可先由学生讲述解题过程，培养学生的语言表达和数学交流能力.接下来由其他同学互评，强调在评价时注重结论是否正确，书写是否规范，是否还有需要完善之处，让全体学生都能正确理解判别式的意义，会用一元二次方程根的判别式判断一元二次方程是否有实数根，以及有实数根时，两根是否相等.

二、教学立意的进一步阐释

1.深刻理解教学内容，精准定位教学目标与重、难点

根据我们对一元二次方程的理解，特别是从根的判别式在后续知识的地位上看，本课的教学内容非常重要.课时教学目标确定为以下两点：第一，理解一元二次方程根的判别式的意义，会用一元二次方程根的判别式判断一元二次方程根的情况；第二，经历一元二次方程根的情况的探究过程，体会从特殊到一般及分类讨论等数学思想，提高观察、分析、归纳的能力.教学重点：理解一元二次方程根的判别式的意义，并能用一元二次方程根的判别式判断一元二次方程根的情况.教学难点：探究一元二次方程根的判别式与一元二次方程根的情况的关系.在确定教学目标、辨明教学重点和难点之后，就可以围绕目标、重点和难点进行选题、构思教学环节.我们常常见到一些课堂教学中选题往往都是因为教学目标的定位不准，造成所选例、习题的内容效度不高，使得训练的重点偏离课时教学目标.

2.引导学生学会观察，深刻理解根的判别式的意义

本课关注的一元二次方程根的判别式是利用求根公式解一元二次方程进程中一个非常关键的“代数式”，教学时要注意引导学生学会观察、找准这个代数式，进而从正、反两个角度深刻理解根的判别式的意义.所选习题也是这两个方面的练习，一是给出系数明确的一元二次方程，通过计算根的判别式判定根的情况；二是给出含待定系数的一元二次方程，通过告知根的情况反过来推定这些系数的值或取值范围.在教学进程中，不但关注学生解出答案，更要关注其是如何运用根的判别式的意义思考问题的，以及思路的出发点在哪儿，通过追问不同学生强调、巩固新知识，达到深刻理解的教学效果.

3.精编例题及变式题，从不同角度训练根的判别式

数学课教学离不开解题，对新授课来说，又不能异化为习题课，所以备课时基于教学目标、重点和难点精心选编例题、选配变式练习跟进训练十分重要.需要指出的是，当前特别是规模较大的学校，因为受到所谓集体备课后“导学案”（多数沦落为习题单式的讲义）牵引，抛开教材、讲评习题成为一种不良现象.新的数学概念或性质的生成需要由一个恰当的问题情境引入，在此基础上，学生参与归纳、生成概念或性质，然后教师根据课前精心选定的例题进行示范，跟进必要的习题巩固并纠正学生解法中的错漏，但是量不能太大，重复习题不能太多，习题太多、太滥容易让课堂成为“无趣”的习题课，特别是大量人为制造的陷阱题，学生练习无趣，反复出错，难以收获解题自信.