2018年广州中考数学压轴题解法探究及反思

广东省广州市第二中学 (邮编：510040)

1 题目呈现

(2018年广州中考数学第25题)如图1，在四边形ABCD中，∠B=60°,∠D=30°,AB=BC.

(1)求∠A+∠C的度数；

(2)连接BD,探究AD、BD、CD三者之间的数量关系，并说明理由；

(3)若AB=1,点E在四边形ABCD内部运动，且满足AE2=BE2+CE2,求点E运动路径的长度.

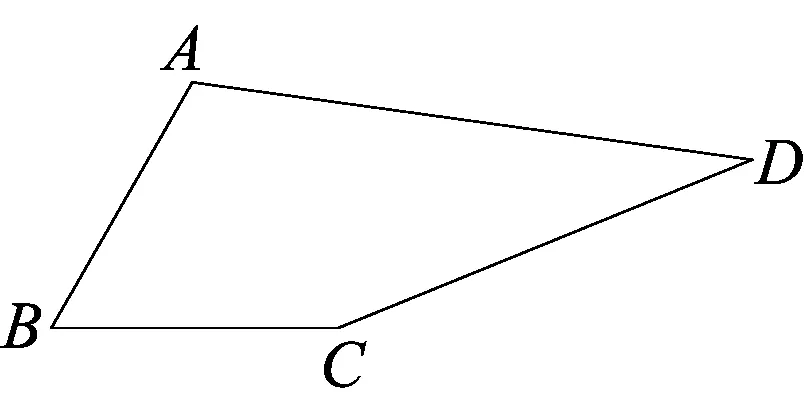
图1

这是一道融合几何三大核心能力(计算、作图、推理)于一体，并且探究性极其丰富的试题，主要考查了四边形内角和、等边三角形、勾股定理、全等三角形、垂径定理、旋转变换等内容.其中第(1)问利用四边形内角和即可求得答案，属于比较简单的问题.第(2)问和第(3)问属于较难的问题，需要学生合理利用辅助线构造全等，综合运用勾股定理、全等三角形、垂径定理等知识进行求解，很多学生在求解这两个问题的过程存在一定的困难.本文主要探究第(2)问和第(3)问的破题思路和解法反思.

2 破题思路

2.1 合理猜想寻思路，旋转变换定方法

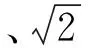
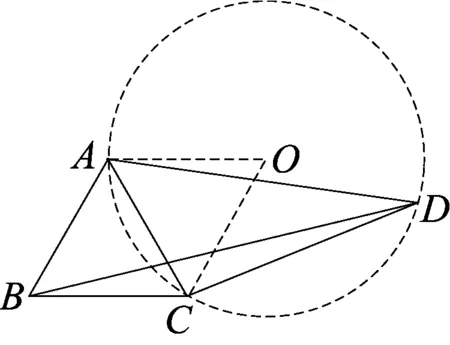
图2

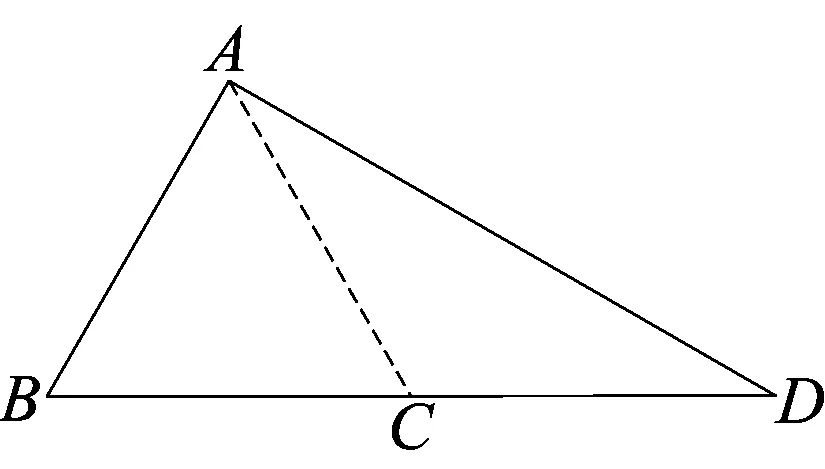
图3

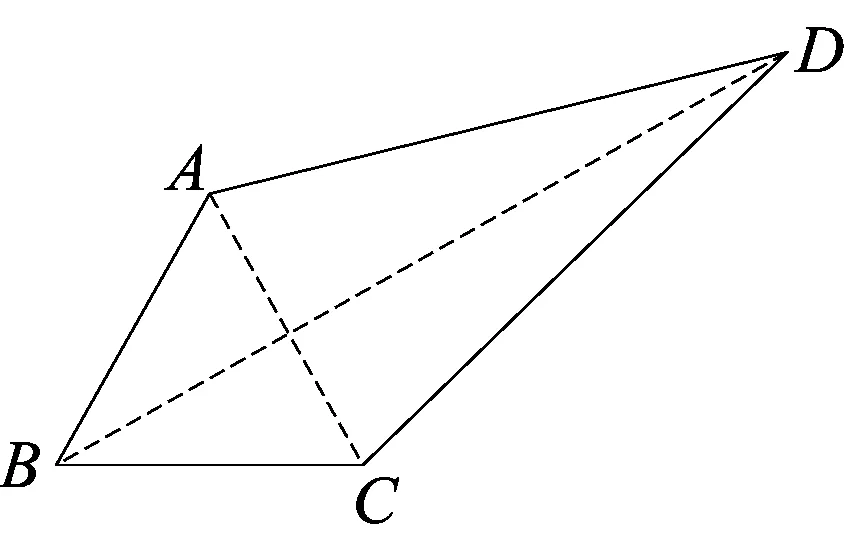
图4

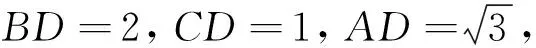
图5

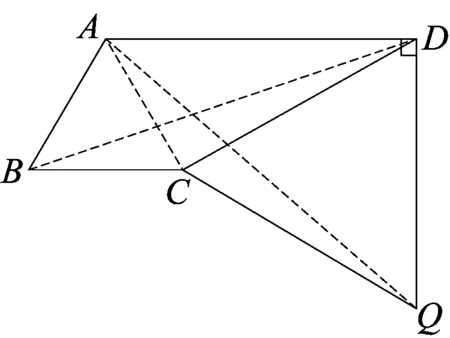
图6

考虑到需要构造直角三角形，即需要让CD边和AD边构造为直角三角形的两条直角边，结合条件“∠D=30°”，不难得出需要以线段AD为边构造等边△ADP(如图5)，或者以线段CD为边构造等边△CDQ(如图6).如图5所示，由等边△ABC和等边△ADP,利用手拉手基本图形可得△BAD≌△CAP(SAS),从而BD=CP.结合∠CDA=30°易得∠CDP=90°,故由勾股定理可得CD2+DP2=CP2,即CD2+AD2=BD2.利用图6的转化方法同样可以证明该结论.

2.2 类比迁移觅良策，灵活运用显威力

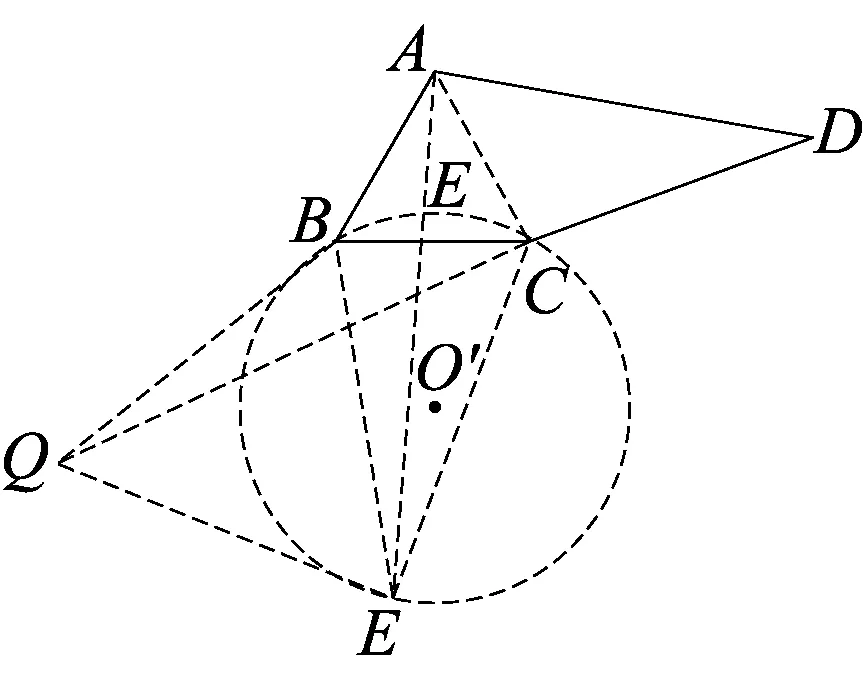
图7

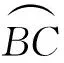
图8

图9

3 进一步研究

3.1 解几思想威力无穷

解析几何是高中阶段核心的学习内容，初中阶段的很多平面几何试题可以利用解析几何的方法进行求解.例如上述问题的第(2)问和第(3)问，如果对辅助线的构造不熟练，则可以采用下面的方法进行求解.

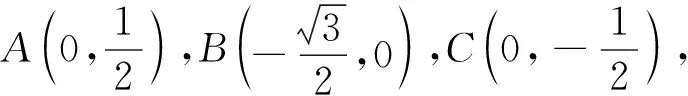
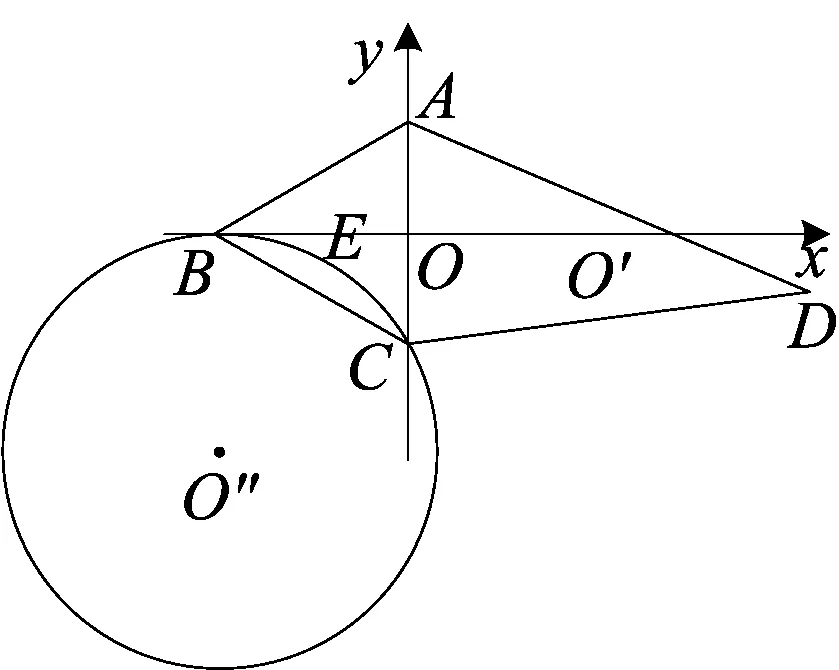
图10

3.2 正余弦定理助力推广

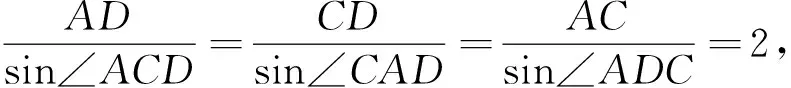
特别地，利用上述解法，我们可以得到如下推广：

推广如图1，在四边形ABCD中，∠ABC=α,∠ADC=β,AB=BC,则：

(1)当α=60°时，则AD、BD、CD满足：BD2=AD2+CD2-2AD·CDcos(60°+β)；

(2)当α=90°时，则AD、BD、CD满足：2BD2=AD2+CD2-2AD·CDcos(90°+β),即2BD2=AD2+CD2+2AD·CDsinβ；

(3)当α=120°时，则AD、BD、CD满足：3BD2=AD2+CD2-2AD·CDcos(120°+β)；

特别地，若α=180°时，则有4BD2=AD2+CD2-2AD·CDcos(180°+β),即4BD2=AD2+CD2+2AD·CDcosθ.

3 解题反思

3.1 凸显核心素养的考查

随着新一轮课程改革，中学数学课程的建设更加注重数学核心素养的渗透.作为指挥棒的中考，中考试题是否能考查出学生的核心素养直接影响着初中阶段的教学导向.所谓数学核心素养，主要指的是以下六方面的数学素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.作为广州市中考数学的压轴题，试题几乎涉及到初中阶段学习到的所有核心内容.学生在求解的过程中，需要综合运用全等三角形、勾股定理、垂径定理、弧长公式等知识进行逻辑推理和运算，还要求学生在求解的过程中作出辅助探究的几何图形，对学生的直观想象能力和作图能力要求较高.若教师在平时的教学中能不断提供有利于落实核心素养的数学课程，相信学生在求解这道试题会更加有信心.

3.2 培养合情推理的能力

对于大部分学生而言，在处理复杂数学问题的时候，除了需要具备克服困难的勇气和意志力以外，还要求学生灵活运用演绎推理和合情推理的方式.合情推理主要指通过观察，归纳，类比，实验，联想，猜测，矫正与调控等方法对问题进行探索，从而寻找得到正确的结论.在解决上面这道中考压轴题的过程中，第(2)问起着承上启下的作用，其解题的方法和思想对整道试题的顺利解决起着关键的作用.在探究AD、BD、CD三者之间的数量关系的过程中，由于题目并没有给出明确的目标，很多学生容易陷入证明一个错误结论的泥潭中.这个时候如果学生能够先利用特殊情况(如点D落在BC的延长线上等)对结论进行合理的想象和验证，则能为正确结论的推理和证明提供非常有利的支持.而这一方面的解题策略有赖于平时学习经验的积累，有赖于教师在平时教学中的不断渗透和引导.

3.3 初高中数学课程的衔接与实验

本文的后半部分利用解析几何的思想和正余弦定理的知识对这道压轴题进行了分析和求解，并且对其作进一步的推广.实际上，这方面的尝试来源于实际教学的需要.在2017年，广州市的四所中学率先实施“2+4初高中一体化实验课程”的实践探索，部分学生在初三的时候开始学习高中的课程内容.在平面直角坐标系、锐角三角函数、直线和圆等初中数学课程的基础上，进一步学习了集合、任意角三角函数，正余弦定理、直线和圆的方程等内容，大部分参与实验的学生均能很好地理解和掌握.在高中阶段，代数式的恒等变形是代数内容的重要学习内容，但限于课时紧而内容多的现实矛盾，高中老师并不会花足够的时间和精力来落实相关训练，很多学生对相关内容的掌握并不尽如人意.若能够在初中阶段的教学中渗透相关的思想和训练，无疑对部分学生而言是非常有益的尝试.本文提供的利用解析几何以及正余弦定理的解法关键也是在代数变形上，这恰好是高中代数内容学习的核心内容.笔者所在学校有幸参加了由朱华伟教授主导的“教育数学创新教学实验”课程实践.实践证明，在初中阶段适当延伸拓展解析几何、正余弦定理等内容对部分初中生的学习是非常必要的.有兴趣的老师可以参考张景中院士的著作《一线串通的初等数学》.