一道课本习题的拓展

安徽省合肥市第六十八中学 (邮编：230601)安徽省合肥市第八中学 (邮编：230601)

对课本的题目进行多方面的拓展、变形，找出在条件不变的前提下，与它平行的结论，和把题中的条件进行适当的变形，得出有关的结论.这样的变式教学既调动学生学习的积极性，又培养学生的创新意识及发现问题和解决问题的能力，从而更有效地培养学生的数学核心素养.下面以一道课本习题为例，以期抛砖引玉.

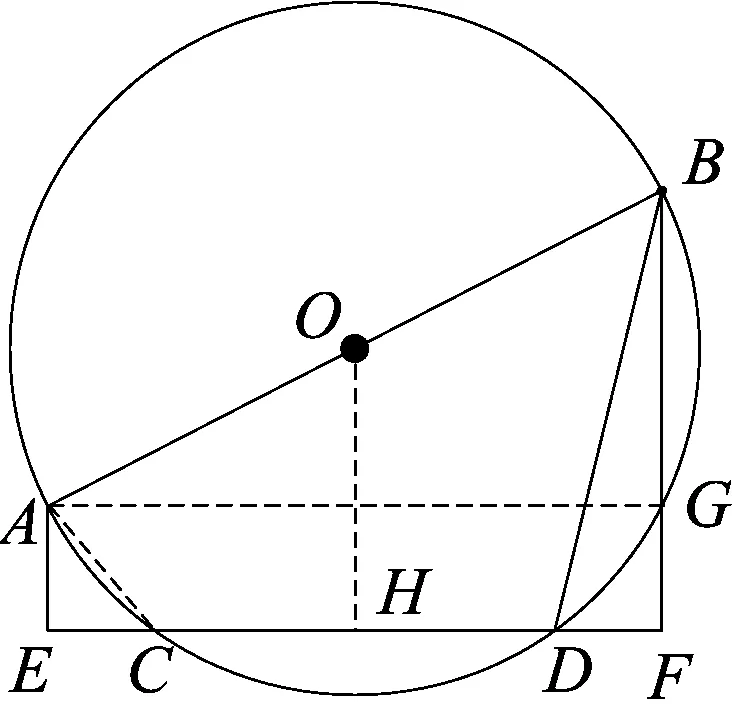
图1

题目已知：如图1，AB为⊙O的直径，EF交⊙O于C、D两点，AE⊥EF，BF⊥EF，E、F为垂足.求证：CE=DF.

分析一般容易想到常用的辅助线(即作弦心距OH)，利用垂径定理和平行线等分线段定理来证明.

证明作OH⊥CD于H，所以CH=DH.

因为AE⊥EF，BF⊥EF，所以AE∥OH∥BF.又OA=OB，所以EH=FH，故EH-CH=FH-DH，即CE=DF.

拓展1这个题目还能得出其它结论吗?

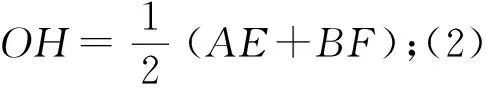
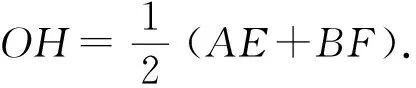
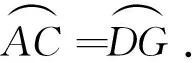
(3)因为AB是⊙O的直径，所以∠ACB=90°，从而∠ACE+∠BCF=90°，又∠ACE+∠EAC=90°，所以∠EAC=∠BCF.

又∠E=∠F=90°，所以ΔAEC∽ΔCFB.

(4)因为ΔAEC∽ΔCFB，所以AE∶CF=EC∶BF，所以CF·EC=ab.又CF+EC=EF=c，所以CF、CE是一元二次方程x2-cx+ab=0的两根.

(5)因为A、B、D、C四点共圆，所以∠BAC=∠BDF，又∠ACB=∠F=90°，

所以△ABC∽△DBF，故(AB+AC+BC)∶(BD+DF+BF)=AB∶BD.

拓展2当把弦CD向上移动时，结论会有什么变化吗？

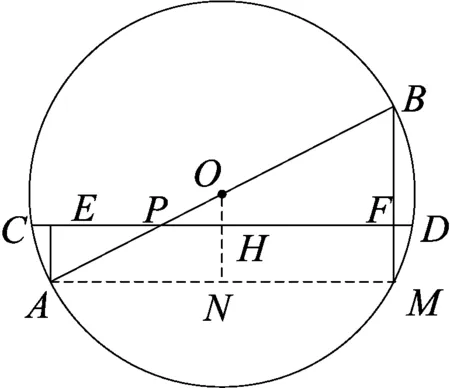
图2

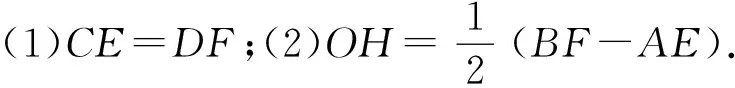
分析如图2，(1)利用垂径定理和平行线等分线段定理来证明(证明过程见上面题目的证明)；(2)延长BF交⊙O于M，连结AM，延长OH交AM于N，利用三角形中位线定理和矩形的性质得证.

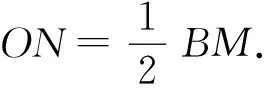
拓展3当把弦CD向下移动时，又会怎样呢？

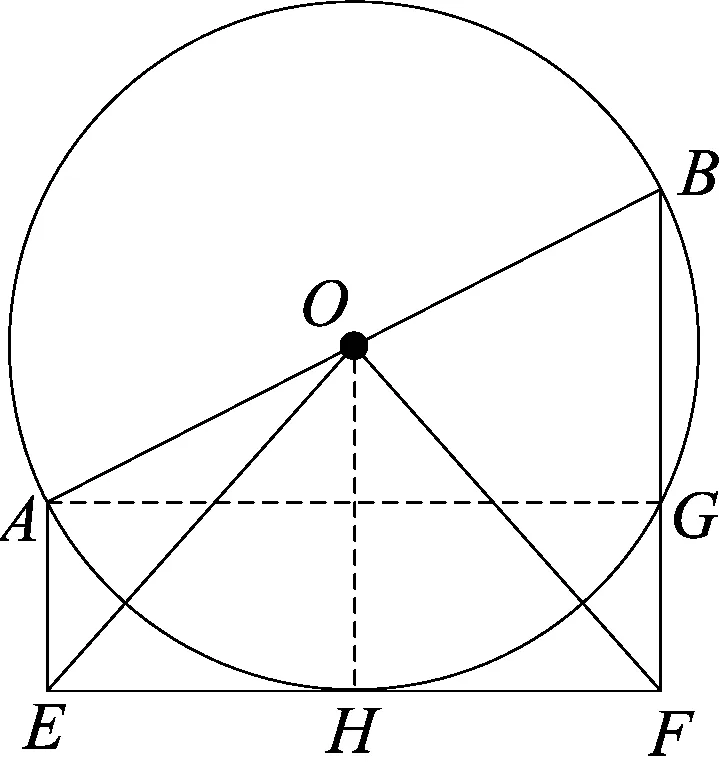
图3

当把弦CD向下移动，使其与⊙O相切于H点(C、D点重合于H)，其它条件不变，结论有：(1)EH=HF；(2)OE=OF；(3)AB=AE+BF；(4)若又知AE=2，BF=3，求四边形AEFB的面积.

分析如图3，(1)利用平行线等分线段定理来证明；(2)利用等腰三角形“三线合一”的性质证明；(3)利用梯形的中位线定理和AB=2OH即可得证；(4)利用梯形的面积公式求四边形AEFB的面积.

证明(1)连结OH，因为EF切⊙O于H，所以OH⊥EF，又AE⊥EF，BF⊥EF，所以AE∥OH∥BH，又OA=OB，故EH=FH.

(2)因为OH⊥EF，又EH=FH，所以OE=OF.

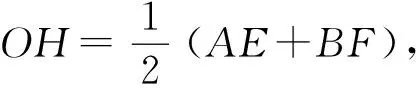
拓展4上述问题的逆命题成立吗？

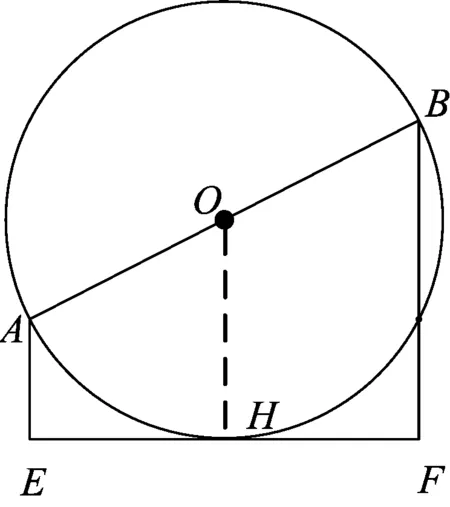
图4

已知AB为⊙O的直径，AE⊥EF，BF⊥EF，E、F为垂足，且AB=AE+BF,求证：EF与⊙O相切.

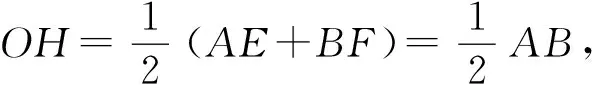
拓展5若在上题中EF与⊙O相切于H，连结AH和BH，其余条件不变，又能得出什么结论呢？

图5

已知AB为⊙O的直径，AE⊥EF，BF⊥EF，E、F为垂足，且EF与⊙O相切于H，连结AH和BH，求证：(1)△AEH∽△BHA∽ΔHFB；(2)EF2=4AE·BF；(3)若设BF=a，AE=c，EF=b，求证：方程x2-bx+ac=0有两个相等的实数根.

分析如图5，(1)证明两角对应相等；(2)利用相似三角形的对应边成比例；(3)利用△=b2-4ac=0.

证明(1)因为AB是直径，所以∠AHB=90°=∠E.

因为EF是⊙O的切线，所以∠AHE=∠ABH，故△AEH∽△BHA.

同理可证△BHA∽ΔHFB，故△AEH∽△BHA∽ΔHFB.

(2)因为ΔAEH∽ΔHFB，所以AE∶HF=EH∶BF，又EH=HF，故EF2=(2EH)2=4EH2=4AE·BF.

(3)因为EF2=4AE·BF，即方程x2-bx+ac=0的判别式Δ=b2-4ac=0，故方程x2-bx+ac=0有两个相等的实数根.

拓展6把上题中的AE⊥EF于E，BF⊥EF于F改为AE⊥AB于A，BF⊥AB于B，情况会怎样呢？

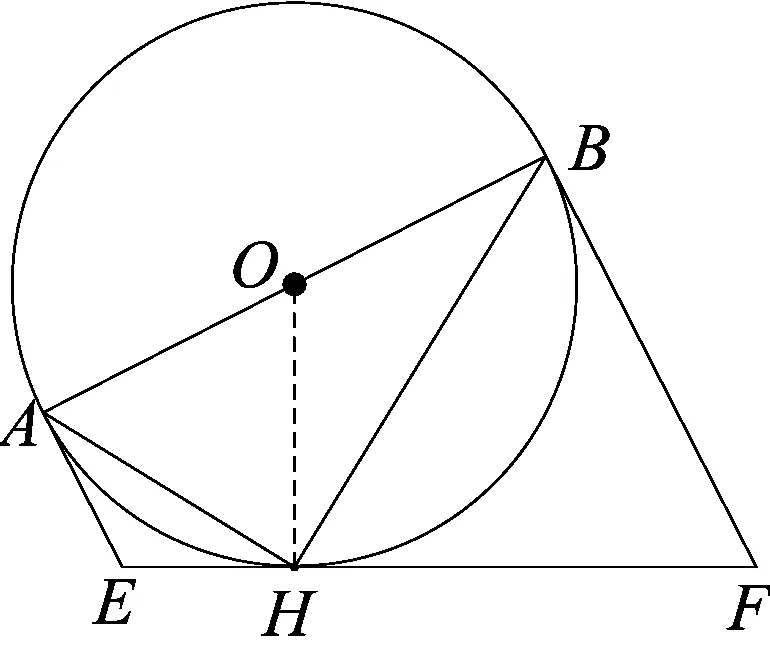
图6

已知：如图6，AB为⊙O的直径，EF切⊙O于H，AE⊥AB，BF⊥AB，A、B为垂足.连结OE、OF，⊙O的半径为R.求证：(1)EF=AE+BF；(2)∠EOF=900；(3)R2=AE·BF；(4)SABFE=R·EF.

分析(1)利用切线长定理；(2)利用全等三角形的性质；(3)利用相似三角形的性质或射影定理，因为OH⊥EF，∠EOF=90°，所以OH2=EH·HF；(4)SABFE=2S△EOF=R·EF.

证明(1)因为AB为⊙O的直径，EF切⊙O于H，AE⊥AB，BF⊥AB，A、B为垂足，所以EA、BF都是⊙O的切线.又EF切⊙O于H，所以EA=EH，FB=FH，故EF=AE+BF.

(2)连结OH，因为△OAE≌△OHE，所以∠EOH=∠EOA，同理得∠FOH=∠FOB，故∠EOF=900.

(3)因为∠A=∠B=90°，又∠EOF=900，

所以∠AOE=∠BFO，所以△AOE∽△BFO，故R2=AE·BF.

(4)因为△OAE≌△OHE，△OBF≌△OHF，故SABFE=2S△EOF=R·EF.

拓展7在上题中，若把连结OE、OF改为连结AF、BE，会有什么结论呢？

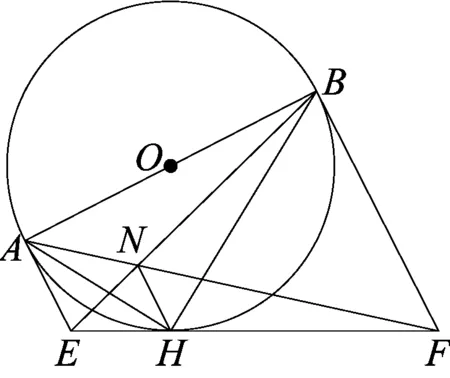
图7

证明(1)因为AB为⊙O的直径，AE⊥AB于A，所以EA是⊙O的切线.又因为EH是⊙O的切线，所以EA=EH.同理可得FB=FH，又AE⊥AB，BF⊥AB，所以AE∥BF，故AN∶NF=AE∶BF=EH∶FH.所以AE∥NH，又因为AE∥BF，故AE∥NH∥BF.

通过对这道习题的深入挖掘提炼，加工改造，变静为动，动静结合，纵横沟通，这道题有七个拓展，每个拓展又有多个问题，这样一个题目就变成了二、三十个题目，从中引导学生理解知识的内在联系，把握解题规律，锻炼学生思维的灵活性、开拓性、多向性和创造性，从而更好地培养学生的探索能力和创新素养.对防止“题海战术”，提高课堂教学效率肯定大有裨益.