直线与椭圆及双曲线位置关系的简易判断法
云南省大理州宾川四中 (邮编:671600)
1 问题的提出
众所周知,直线l与圆⊙C的位置关系最简单的判断方法是:用圆心C到直线l的距离d与半径R的关系得出,即当且仅当
(1)d>R时,直线l与圆⊙C相离;
(2)d=R时,直线l与圆⊙C相切;
(3)d 由于椭圆与双曲线都有对称中心,是有心曲线,这点与圆一样,所以,我们自然希望也能用椭圆及双曲线的中心到直线l的距离d来判断直线与椭圆及双曲线位置关系,经过探索我们得到一个简便的判断方法. 2.1 本文中有关的符号说明 我们把椭圆的长半轴长及双曲线的实半轴长记为a,椭圆的短半轴长及双曲线的虚半轴长记为b,椭圆与双曲线的半焦距记为c,直线l与椭圆或双曲线焦点所在直线的的夹角记为θ(00≤θ≤900),直线l的倾斜角记为α(00≤α<1800),曲线中心到直线l的距离为d. 注不难得到焦点在x轴上总有cos2θ=cos2α, 焦点在y轴上总有cos2θ=sin2α. 2.2 直线与椭圆位置关系的判断 定理1设f(θ)=a2-c2cos2θ,则当且仅当 (1)d2>f(θ)时,直线l与椭圆相离; (2)d2=f(θ)时,直线l与椭圆相切; (3)d2 ① ② 计算得方程②的判别式△=4a2b2(b2+a2k2-m2) ③ ④ 综上,定理1成立. 2.3 直线与双曲线位置关系的判断 (1)d2>f(θ)时,直线l与双曲线相交; (2)d2=f(θ)时,直线l与双曲线相切; (3)d2 ⑤ ⑥ 计算得方程⑥的判别式 △=4a2b2(m2+b2-a2k2) ⑦ ⑧ 综上,定理2成立. 例1已知椭圆E的两个焦点F1(-3,0),F2(3,0),且椭圆E与直线l:x-y+9=0有公共点,求椭圆E长轴最短时的方程. 计算得 解由题意知, 计算得 如果把f(θ)=a2-c2cos2θ看成R2,那么,直线与椭圆的位置关系的判断方法几乎与直线与圆的判断方法一样,对于双曲线而言,由于中心在曲线外,除相切外,相离与相交的结论与椭圆相反.2 结论的形成及证明
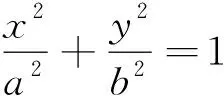
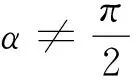
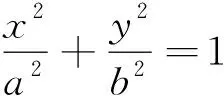
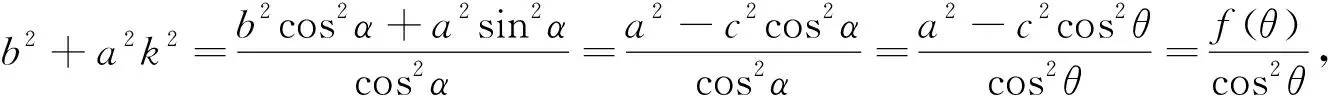
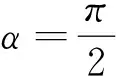
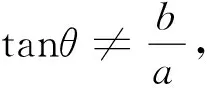
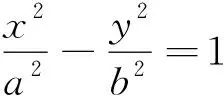
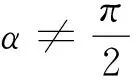
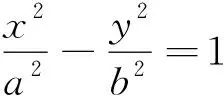
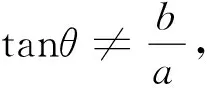
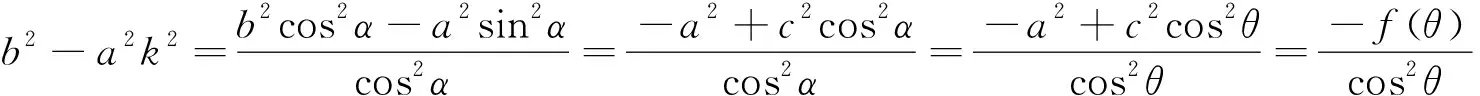
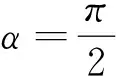
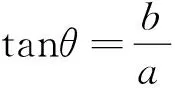
3 结论的运用
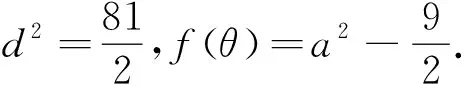
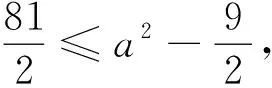
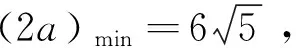
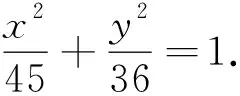
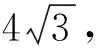
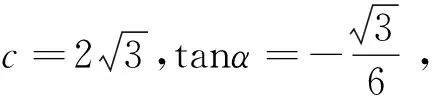


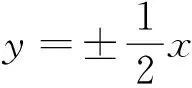

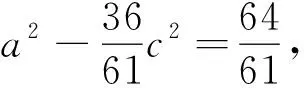
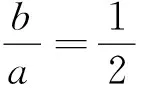
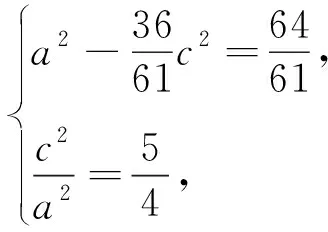
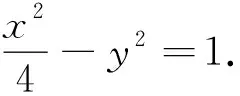
4 记忆方法
——对2018年广州市一道中考题的研究

