风力机盘式制动器的热-结构理论模型分析

刘海玲，殷玉枫，鹿传财，高崇仁

(太原科技大学 机械工程学院 太原 030024)

随着经济的增长，风力机行业迅速发展，但是，目前我国对风力机制动器的研究还没有成熟，严重制约着我国风力行业的发展。风力机制动器在制动过程中，制动器的温度和应力是瞬态变化的，同时风力机制动器的温度和应力是相互影响的。研究温度场和应力场的耦合分析是分析风力机制动器寿命的重要前提，是制动器材料选择的重要依据。

J.R.Barber[1]等研究分析了热弹性不稳定的问题，通过实验得出热弹性不稳定现象对制动盘的制动性能有着非常重要的影响，同时也得到了制动盘和摩擦衬片的“hot spot”的分布，得到了热弹性不稳定现象的临界瞬时速度。Voldridllsliy[2]研究了摩擦表面的相对速度，通过与临界滑动速度相比，发现了制动盘表面“hot spot”形成的主要原因，同时还发现制动盘的热疲劳破坏有可能也与“hot spot”有关。Mesut Duzgun[3]建立了通风制动器三维模型，分析了在制动器重复连续制动的情况下通风制动器的热行为，分析了不同的三种方案。

国内在研究制动器的制动过程时，主要关注于制动器的温度场的分布，对制动器的耦合特性范畴的研究较少，所以国内的有关的研究集中在制动器的温度场的分布。李亮针[4]建立了有限元模型，并通过实验验证了模拟的结果，同时分析了盘式制动器接触界面的温度场、应力场和热变形等很多原因，分析结果表明盘式制动器接触界面上的压力分布并不均匀。张立军等[5]对不同厚度的制动盘测量其温度和几何形变，分别分析了制动盘的制动压力和制动盘的几何特征对制动盘热应力耦合结果的影响。实验结果表明：制动盘发生几何形变的主要原因是制动盘制动过程中温度的升高，制动盘不同厚度对制动盘温度也有一定的影响。杨智勇等[6]通过试验，结果表明建立有接触模型的热—机耦合的模型，模拟出的结果更符合实际情况，模拟结果显示，制动盘在制动过程中热斑的分布是不均匀的，这是因为制动盘局部的压力过大导致的，这也导致了在制动盘上温度和应力分布的不均。

1 风力机热-结构耦合有限元模型的建立

1.1 风力机热传导模型的建立

1.1.1 风力机制动器热流密度的分配

风力机制动器的热载荷主要来源于摩擦产生的热流密度，摩擦表面的热流密度满足公式：

其中：q(x,y,t)——输入的热流密度；

η——制动副摩擦系数；

p(x,y,t)——摩擦表面比压；

υ(x,y,t)——摩擦盘和衬片的相对速度；

F(x,y,t)——制动压力；

S——摩擦衬片有效接触面积；

ω——制动盘角速度；

r——摩擦盘和衬片有效作用半径。

制动器摩擦表面的热流密度满足公式：

q(x,y,t)=qd+qp(2)

(3)

其中：k为热传导系数；ρ为密度；

1.1.2 风力机制动器的热传导方程

风力机在制动时，摩擦衬片固定不动，而制动盘作逆时针转动，制动盘没有内热源。风力机摩擦盘和衬片分别在直角坐标下的热传导方程：

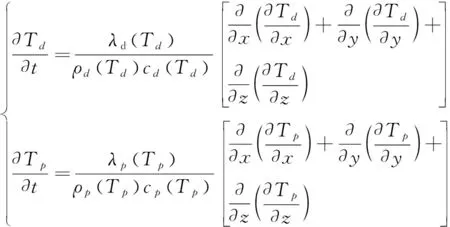
(4)

其中：cd，cp——风力机制动盘、衬片的比热容

λd，λp——风力机制动盘、衬片的热导率，

Td，Tp——风力机制动盘、衬片的温度

t——风力机制动时间

1.1.3 风力机制动器的初始条件和边界条件

(1)初始条件

风力机在没有制动之前，认为制动器与周围环境的温度是相同的，即温度场的初始温度就是周围环境的温度，我们较常用的环境的温度为一年内温度的平均值，认为制动器的初始条件为：

T0=Tf(5)

T0——风力机盘式制动器的初始温度；

Tf——环境温度，环境温度为20 ℃.

(2)边界条件

制动盘和摩擦衬片的边界条件采用第三类边界条件，即已知制动盘和摩擦衬片表面与周围环境产生的热量交换。

对于制动盘来说，摩擦界面、中间界面和其他界面作为主要的换热界面，摩擦界面是制动盘和摩擦衬片相接触的那部分表面。这部分表面只承受热载荷，即热流密度，这部分表面的边界条件为热流密度、热传导和热辐射，其数学表达式为：

(6)

其中：hd——制动盘的换热系数；

Td——风力机制动盘的温度；

Tp——风力机摩擦片的温度；

A——辐射面积；

σ0——斯特芬玻尔兹曼常数。

中间界面是除了摩擦界面之外的与周围环境不接触的界面，故其只承受制动盘的热传导，所以中间界面的边界条件为热辐射以及与空气的对流换热，数学表达式为：

其他界面也就是除了摩擦界面和中间界面之外的界面，也就是制动盘与周围环境相接触的表面，所以主要承受与周围环境的对流换热和热辐射，所以其他界面的边界条件为对流换热和热辐射，数学表达为：

边界条件对于摩擦衬片来说，与制动盘的边界条件是相似的，也可以分别分为三个部分，即摩擦界面、中间界面和其他界面，界面的范围也是类似的。摩擦界面是摩擦衬片上与制动盘相接触的表面；而中间界面是除了摩擦界面之外的摩擦衬片上不与周围环境相接触的表面；而其他界面就是除了摩擦界面和中间界面之外的摩擦衬片上的其他表面。摩擦衬片上不同的界面的边界条件与制动盘的相对应的界面上的边界条件是相似的。

1.2 风力机盘式制动器热应力的计算

假设风力机盘式制动器在制动过程中只发生了线弹性变形，但形状保持不变。则剪应变为0，因为温度变化产生的热应变为αΔT，即：

(9)

其中：

α——线膨胀系数；

ΔT——物体升高的温度；

不考虑温度场产生的热应变时，制动器的应变为：

其中：εx、εy、εz——风力机制动器在x、y、z三个方向上的应变；

γxy、γyz、γxz——风力机制动器在x、y、z三个方向上的剪应变；

σx、σy、σz——x、y、z方向的正应力；

τxy、τyz、τxz——对应平面的切应力；

E——风力机制动器的弹性模量；

G——风力机制动器的剪切模量；

μ——风力机制动器的泊松比。

若是考虑到热应变，风力机盘式制动器的应变就必须加上热应变，公式(10)变成了：

其中：

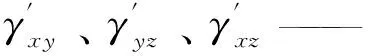
根据弹性力学理论，可以得到风力机盘式制动器热—结构耦合下的应力σ′和应变ε′之间的关系：

σ′=Dε′(12)

D——风力机制动器弹性矩阵。

2 风力机盘式制动器热-结构耦合流程图

风力机制动器温度分布不均，将导致制动器发生热弹性变形，而热弹性变形也会对风力机的温度产生影响，所以制动盘的温度和应力之间不是独立存在的，而是相互影响的。图1是风力机制动器温度场、应力场、变形之间的耦合关系流程图。

图1 风力机制动器温度场、应力场、变形之间的耦合关系图
Fig.1 The coupling relationship of temperature field, stress field and deformation of wind turbine brake

3 风力机盘式制动器热-结构模拟结果

3.1 风力机摩擦衬片应力场的模拟结果

利用ansys有限元软件模拟风力机盘式制动器制动器温度和应力的分布情况。风力机摩擦衬片的等效应力分布如图 ：

图2 风力机摩擦衬片的等效应力分布
Fig.2 Equivalent stress distribution of wind turbine friction lining

从图2可以看出：对于制动衬片而言，从制动开始到制动结束，制动衬片接触表面的温度一直升高，并且温度分布则是一直具有明显的等值线。整个制动过程中，制动衬片的最高温度是一直上升的，并且最大温度一直在摩擦面的最外端部分，这是因为在整个制动过程中，这部分区域一直受最大摩擦热流的作用，而且因为制动衬片的摩擦面一直紧贴制动盘的表面，所以这部分区域不受散热以及热辐射影响,因而温度会一直升高。而摩擦衬片四周表面也吸收储存了差不多相同多的热量，产生的温度梯度是很小的，所以摩擦衬片中心的热量扩散的很慢。而摩擦衬片四周因为与周围空气的强制热对流和热辐射，相对来说扩散的热量相对较多。

3.2 风力机制动盘的温度场和应力场模拟结果

图3 风力机制动盘的温度分布
Fig.3 Equivalent stress distribution of wind turbine friction lining

从图3可以看出制动盘表面温度的分布是不均匀的，制动盘外侧的温度最高，内侧的温度最低。摩擦衬片与制动盘的摩擦区域主要集中在制动盘的外侧，所以温度最先升高的区域也在制动盘的外侧，同样的制动盘外侧也是温度升高的最快的区域。制动盘内侧因为没有摩擦产生的热量，温度的升高主要依靠制动盘外侧与内侧的温度产生的温度梯度造成的热传导，所以制动盘内侧的温度升高的也不快。

随着时间的增加，摩擦产生的热量急剧增大，风力机盘式制动器的短时间内无法完全使这些热能消散，所以制动盘的温度也随着制动时间的增加而增加。制动盘的温度的较高点主要分布在制动盘与摩擦衬片的接触摩擦处，这是因为在这些区域温度的升高主要是因为制动盘和摩擦衬片间的摩擦生热，而非接触摩擦区域的温度主要是因为接触摩擦处比非接触摩擦处的温度高，产生了温度梯度，接触摩擦处的温度通过温度的传递到非接触摩擦处，所以非接触区域的温度远远低于接触摩擦处的温度。从整个制动盘来看，温度的分布是不均匀的。

在制动盘盘面上沿制动盘的径向方向节点，得到风力机盘式制动盘表面的温度沿制动盘径向方向的变化曲线。从图中可以看出温度最大为469.128 ℃，温度的分布沿着径向方向先升高再下降。这是因为制动盘温度较高的区域为摩擦制动的区域，而温度较低的区域为非摩擦区域，也就是从制动盘摩擦区域到摩擦区域再到非摩擦区域。在距离为1.4左右制动盘的温度开始有明显的趋势，上升的趋势一直持续到3.7左右，之后开始下降。而到5.4左右的地方，制动盘的温度下降到了80 ℃左右。而制动盘最外面的表面的温度为71.942 ℃.

图4 风力机制动盘表面温度沿径向的变化曲线
Fig.4 The radial surface temperature of wind braking plate

4 结论

(1)风力机制动盘不同表面有不同的边界条件。摩擦衬片的应力随着制动时间的增加而增加。

(2)风力机制动过程由温度场和应力场共同作用的，不是独立存在的，两者存在耦合关系。

(3)风力机制动盘在接触摩擦区域的温度和应力最大。同时制动盘和摩擦衬片的温度和应力分布都不均匀。