基于寿命空间划分的多部件系统维修决策

王玉亮，张晓红，曾建潮,2

(1.太原科技大学 工业与系统工程研究所，太原 030024；2.中北大学 计算机与控制工程学院，太原 030051)

目前，多数维修决策研究都是将基于TBM建模理论或者基于CBM建模理论与机会维修相结合的维修策略。机会维修策略是指在系统中的某个部件失效或者需要进行维修的同时对即将失效的某些个部件同时进行维修。Bergman[1]最先针对两相同部件提出了机会更换策略。文献[2-3]研究了将TBM与机会维修相结合的维修策略，其中文献[4-5]研究了在系统预防性维修之前发生故障时采用最小维修与机会维修相结合的维修策略。文献[6-9]将CBM与机会维修相结合建立了视情机会维修模型，并且最后寻求一种优化算法得到使得系统成本最低的状态阈值。高坤等[10]研究了基于CBM的轧辊维修策略的与备件库存的联合优化问题。

然而，此类文献并未给出统一的建模方法，对于一个崭新的多部件系统需要重新进行建模研究，既费时又费力。2015年，张晓红和曾建潮针对由多个相同[11]/不相同[12]的部件组成的系统，提出了一种多部件系统通用的状态空间划分建模方法，研究了相同/不相同多部件系统的维修优化问题。但文献[11]和文献[12]中考虑了退化增量分布建模的CBM决策模型。

本文将退化状态空间划分方法应用到多部件系统联合寿命空间的建模研究中，针对多部件系统提出了年龄机会更换策略，对任意M部件系统的联合寿命空间进行统一的划分与建模，然后，以两部件系统为例，研究了系统的基于TBM的维修优化决策问题。

1 系统的特征描述及假设

1)系统在每次需要维修时，只需要花费一次固定的费用Cset，只与维修的次数有关；

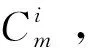
假设系统的单位时间停机成本为Cd.

2 联合寿命空间划分与建模

图1 单部件系统的寿命空间划分
Fig.1 Lifetime space partition of single-unit systems

图2 两部件系统的寿命空间划分
Fig.2 Lifetime space partition of two-unit systems

3 联合寿命分布

3.1 联合寿命分布的定义

单部件系统的维修更换过程是全更新过程，然而，在多部件系统中，经历一次维修之后，系统中部分或是全部部件恢复到初始状态，遵循半更新特性。因此，借助系统的半更新特性，推导系统联合寿命的稳态联合概率密度函数。

设部件i的寿命Ti～fi(t)，遍历整个寿命空间，下面以两部件系统为例分析求解系统任意两次更换活动之间的稳态联合寿命分布g(t1,t2).

系统第k-1次更换前的寿命向量为tk-1=(τ1,τ2)，更换后寿命向量为tk-1'=(τ1',τ2')，运行一个半更新周期后的寿命向量为tk=(t1,t2).根据所定义的年龄机会更换维修策略，第k-1次的系统更新情况的分析如下：

(1)更换系统中的全部部件。更换维修后tk-1'=(0,0)，若用R12表示两部件全部更换的事件：

(1)

(2)只更换系统中的部件1，在经历了维修后系统的寿命向量为tk-1'=(0,τ2).用R1表示在第k-1次更换时只对部件1进行预防性更换的事件，分以下两种情况分别讨论：

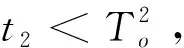
总之，事件R1发生的概率可以表示为式所示：

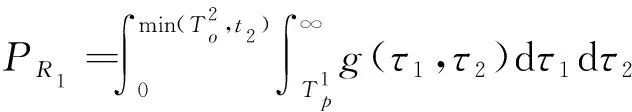
(2)

该情况所发生的概率可表示为式所示：

(3)

综上，系统在发生第k次更换前系统的寿命向量为Tk=(t1,t2)的概率可表示为式：

g(t1,t2)=

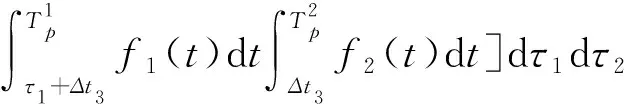
(4)

3.2 稳态联合寿命分布的求解

根据两部件系统的寿命空间划分方法可得到式所示的关系：

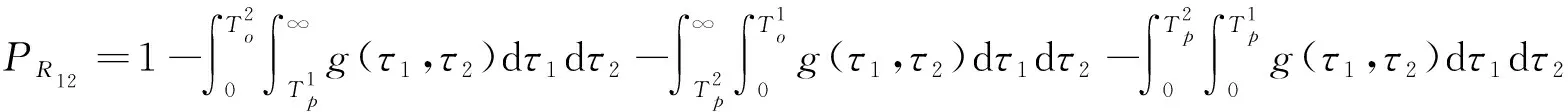
(5)

将式所示的关系、式所示的全概率公式和式中的正交近似数值求解规则相结合，可以得到式:

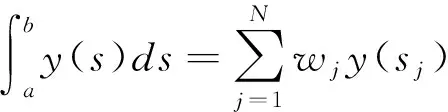
(6)

要求解的两部件系统的联合稳态寿命分布函数可用向量形式Gimax×imax=(G1,G2,…Gi,Gmax)'表示，其中矩阵Gi是一个1行imax列的向量，并且每个可以表示为Gi=(g(ih1,h2),g(ih1,2h2)…,g(ih1,jh2),…g(ih1,imaxh2))，式可改写为式所示的向量的形式：

G+K1G+K2G+K3G-K4G-K5G=b⟹

(I+K1+K2+K3-K4-K5)G=b

(8)

利用MATLAB数值实验所求得的式中矩阵G即为本节中所定义的稳态概率密度函数g(t1,t2)的数值近似解。

4 费用率模型

4.1 模型的建立

1960年，Barlow和Hunter[13]定义了长期时间内的平均费用率：

(9)

其中E(T)表示的是系统的半更新周期的期望，E(C(T))表示的是系统全部维修活动所产生的总成本的期望。一个半更新周期T应该包括两次维修之间的系统运行时间T'和维修停机时间D两部分。即：

E(T)=E(T')+E(D)

(10)

在系统的任意的时刻全部的维修活动以及其发生的概率和产生的成本如下：

(1)系统中只有一个部件进行更换产生的成本：

(2)系统中有两个部件同时进行更换产生的成本：

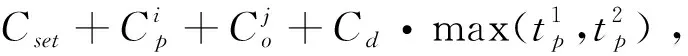
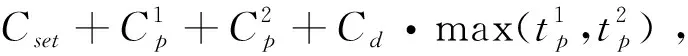
(3)系统中最小维修的成本：

根据制定的维修策略，若部件在系统更换时刻之前发生了故障需要对其进行最小维修，只产生最小维修的费用，因此，在每一个半更新周期内小修的次数计算如下：

综合以上分析，系统的维修成本的平均期望为式：

E(C(T))=

(12)

系统的平均维修停机时间可表示为：

(13)

系统的运行时间的期望是

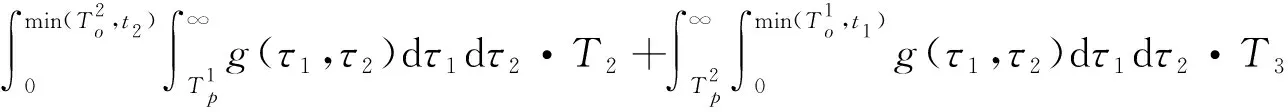
其中

综合以上的分析，系统的费用率模型可表示为式的带约束的数学优化问题：

(14)

4.2 模型的求解及数值实验

式是一个含有约束函数的优化模型不能通过简单的数学解析法求得最终的最优解。遗传算法是一种全局优化算法，因此，本文采用遗传算法进行寻求最优解。

为了验证本文提出方法的有效性和正确性，取文献[14]中某风场变桨系统关键部件进行验证该方法的正确性：电气滑环和元器件两个部件，寿命分别服从参数β1=1.116，θ1=151.3908和β2=1.057，θ2=223.3989的威布尔分布。

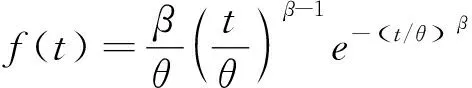
(15)

其中β为形状参数，θ为尺度参数。

图3 预防性更换阈值对费用率目标的影响
Fig.3 Effects of opportunistic maintenance thresholdson the expected cost per unit time

由图3和图4可知在更换阈值不断变化的过程中，都存在一个使得系统费用率最小的极值点。由于部件1与部件2具有对称性，可知部件1也存在一个使得系统费用率最小的极值点，因此，系统存在一个权衡点能够使得系统的费用率最低。

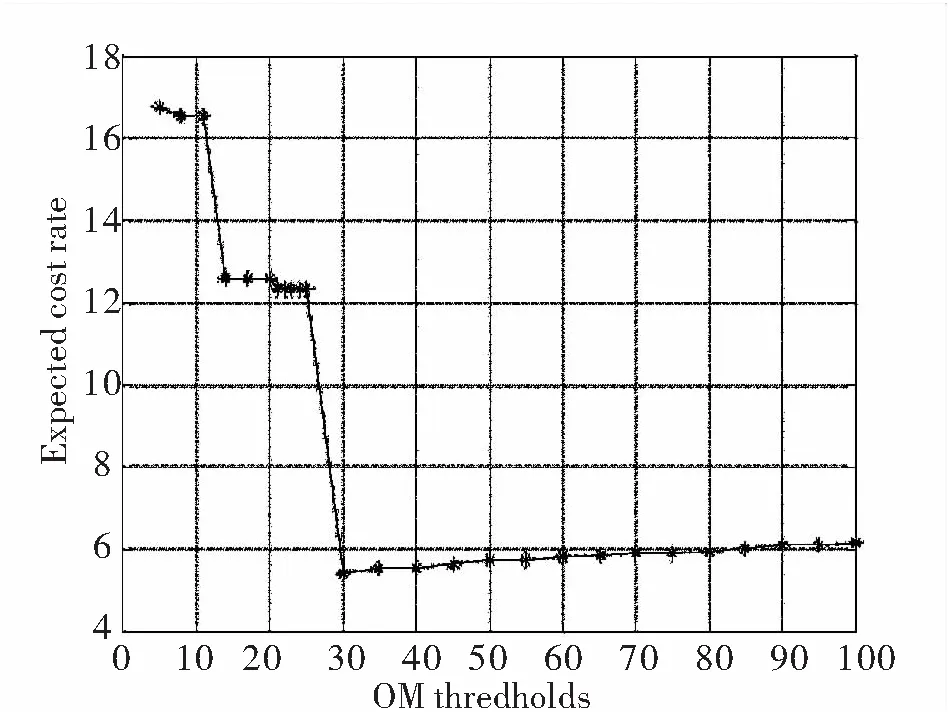
图4 机会更换阈值对费用率目标的影响
Fig.4 Effects of opportunistic maintenance thresholdson the expected cost per unit time

图5 遗传算法一次示例进化优化过程
Fig.5 An example of optimization result of GA

5 结束语

将退化状态空间划分方法应用到多部件系统联合寿命空间的划分建模研究中，提出基于TBM的机会维修策略，以两部件系统为例定义并推导了多部件系统的联合寿命分布，给出了相应地数值解法，以此为基础，建立了系统长期的费用率模型，最后通过遗传算法优化求解得到最优的更换维修阈值。

接下来可考虑更加符合实际的非完美维修的多部件系统的联合寿命空间的划分建模研究以及剩余寿命空间的划分建模或者将本文的研究继续深入到系统的维修备件库存的内容中去。