常见三角函数数学思维方式的养成和探究

赵熙瑞

摘要： 三角函数是高中数学中的基础知识，其思维方式十分灵活多变，其思索过程能够培养人们深刻、高效的逻辑推理能力。因此，本文以三角函数为例，通过案例分析的方式，探索其常见的数学思维方式，并探讨养成良好思维方式的基本措施，最后对各种思维方式的运用提出建议。

关键词： 三角函数;思维方式;案例分析

中图分类号： G633    文献标识码： A    文章编号： 1672-9129（2018）09-0166-02

Abstract：   trigonometric function is the basic knowledge in high school mathematics. Its thinking mode is very flexible， and its thinking process can cultivate people's profound and efficient logical reasoning ability. Therefore， this paper takes trigonometric function as an example， explores its common mathematical thinking mode through case analysis， discusses the basic measures to develop a good thinking mode， and finally puts forward Suggestions on the application of various thinking modes.

Key words：  trigonometric function; Mode of thinking; Case analysis

1 引言

三角函数是高中数学的重点和难点部分之一，高中阶段的学习包括正弦、余弦及正切三种，需要高中生加以全面掌握。三角函数题型变化多样，思维方式也十分广泛。目前，以三角函数思维方式为研究方向的相关论述较多，研究者们从多种角度对三角函数的思维方式加以归纳整理。但是，现有的研究成果往往只考虑了三角函数的思维方式，并没有从深层次对培养思维方式的措施进行分析。因此，本文以三角函数的经典题型的解析出发，对三角函数常见思维方式（联想思维、变换思维和图像思维）进行归纳分析，并从反思能力、创新能力和实践能力的角度提出培养三角函数思维方式的具体措施。

2 三角函数常见思维方式及案例分析

2.1联想思维方式及案例分析。所谓联想思维方式，就是由一个问题联想到另一个相关的问题，从而将后一个问题的解决思路运用到前一个问题当中，从而最终解决问题。这一思维方式，在数学研究当中十分常见，是解决数学问题的重要桥梁。而在三角函数中，采用联想思维方式解决问题的模式十分常见和有效。

例题：在△ABC中，内角A，B，C所对边分别为a，b，c，cosB=4/5，若c=2a求sinB/sinC的值。

解法：在△ABC中，因为cosB=4/5，

所以（a2+c2-b2）/2ac/2=4/5

因为c=2a，

所以[（c/2）2+c2-b2]/2c×c/2=4/5，即b2/c=9/20，

所以：b/c=3√5/10，

由正弦定理得sinB/sinC=b/c

所以：sinB/sinC=3√5/10

从上述例题的解题过程可以看到，解题者可以从三角函数中cosB的数值开始，联想到三角形中对应的边的比值，从而找到解题思路。联想思维方式的应用，有助于培养学生的发散思维，从而提高思维的灵活性。

2.2变换思维方式及案例分析。变换思维方式在三角函数中应用广泛，三角函数问题的解决多依靠于利用切弦转化、降幂公式、二倍角公式及正余弦定理对原函数进行变换，将已知信息与问题进行量化联系，从而解决三角函数问题。

例题：已知cos（π/6-α）=2/3，求sin（α-2π/3）的值。

解法：因为cos（π/6-α）=2/3，且（π/6-α）+（α-2π/3）=-π/2，

所以sin（α-2π/3）=sin[-π/2-（π/6-α）]=-sin[π/2+（π/6-α）]=-cos（π/6-α）=-2/3

从上述例题的解题过程可以看到，解题者可以利用诱导公式，将所求函数与已知函数相联系，从而抓住解题要点。变换思维方式注重学生对各公式的理解和熟悉程度，有利于学生对题目进行重点剖析，提升思维的准确性。

2.3图形思维方式及案例分析。在函数问题的解析过程中，其图形思维方式即由函数的解析式作出图像，通过图像特征简便求解函数单调性、值域、极值、最值等内容的解题方式。这种解题思路有利于快速对陌生函数进行初步了解，从而解决较为复杂的函数问题，在三角函数的解题过程中应用十分广泛。

例题：求解f（x）=sinx/sinx+2的值域

解法：令t=sinx∈[-1，1] 则g（t）=t/t+2=1-2/t+2

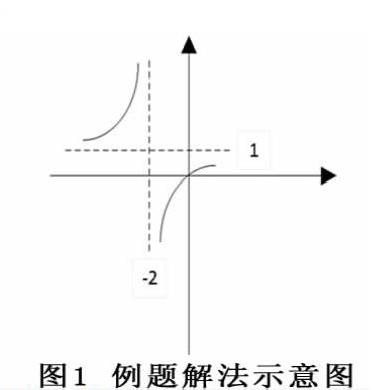
然后建立平面直角坐标系，作出类反比例函数图象如图1所示。

由图可得，值域为[-1，1/3]

从上述例题的解题过程可以看到，解题者可以通过换元方式将函数进行简化，从而做出函数的图像，并依据图像进行快速解题。通过对图形思维方式的应用，学生可以掌握三角函数快速解题的技巧，从而提高思维深度。

3 培养思维方式的措施

3.1培养反思能力。在三角函数的解题过程中，学生可以从现有题目解题过程进行总结和反思，尤其是可以对错题的解题过程进行逐步对照，找出自己在解题过程中出现错误的根源，从而避免下次在面对同类型题目时出现类似的错误。

3.2培养创新能力。三角函数问题中常需采用发散性思维解决问题，学生可以对旧题进行思考，寻找新解法，找出最优解，从而加深对题目的理解，拓展解题思维能力，并有利于培养和锻炼创新思维能力。

3.3培养实践能力。为进一步加强解题能力，学生可以通过探究和实践的方式，对三角函数各题型进行整理，并通过与自己所掌握的知识体系进行对比，从而找出知识盲区，总结解题方式，掌握三角函数解题技巧。

结论：本文从三角函数常见的联想、变换和图形思维方式出发，通过具体的案例，分析思维的过程，从而培鍛炼学生在三角函数领域思维的灵活性、准确性和思维深度，并从反思能力、创新能力和实践能力的角度提出培养思维方式的具体措施。

参考文献：

[1]曹梦炘.论述高中数学三角函数公式的运用[J].考试周刊，2017（13）：49-51.

[2]金雪亚.在公式变式训练中培养学生的数学思维能力——例谈《二倍角的三角函数》[J].数学学习与研究，2015（9）：93-93.

[3]孟祥秀.浅论高中生学习能力在三角函数教学中的培养[J].考试周刊，2014（6）：56-57.

[4]唐小惠.观察·联想·变形·统一——浅谈三角函数教学中思维品质的培养[J].数学教学研究，1997（4）.

[5]许海林.三角函数教学中学生思维能力的培养探究[J].数理化学习（高三版），2014（8）：56-56.

[6]张大胜.数学思想方法在三角函数中的应用[J].语数外学习（高中版上旬），2015（1）.