集合、逻辑、函数知识结构与方法拓展
■河南省信阳市职业技术学院 万永鹏
一、知识结构

二、结构分析
(1)数学是一门理性的科学,她有两个主要标志,一是公理化,二是符号化,因而学习数学必须打好两个基础:逻辑与集合。逻辑关注的是数学思维与表达,最小单位是命题。集合强调概念学习的标准化与符号化,以及多种数学语言之间的转换,最终目标是研究集合之间的关系。一纲、一目互为交织,使数学知识具有系统化的结构。
(2)高中数学知识中,函数是首要的核心概念,由它引发的知识体系、方法体系、思维体系支撑了数学的主要框架,因此,抓住函数,扎实打好基础是学习数学的“捷径”。
(3)对于函数概念的学习,要从对应出发,它是建立在两个非空数集的特殊对应,即任意一个自变量值x只对应唯一一个因变量值y,这种对应有稳定性、确定性,甚至可以用等式(方程)表达,于是可以由一个变量控制另一个变量,从而产生广泛的应用。
(4)函数性质的学习是对概念学习的深化。基本初等函数的学习是知识应用的具体化,因此要强化指数、对数、三角运算的学习与训练。
三、展例释理
例1 对于函数f(x),若f(x)=x,则称x为f(x)的“不动点”,若f[f(x)]=x,则称x为f(x)的“稳定点”;记A={x|x为f(x)的不动点},B={x|x为f(x)的稳定点}。
(1)探究:A与B是否具有包含关系,为什么?
(2)已知f(x)=a x2-1,命题p:∃x0∈R,使A与B至少有一个为∅。若p为假命题,求实数a的取值范围。
分析:(1)探究可以从特例出发,但作为解答题,需要证明,于是要从包含关系的定义着手。(2)因为p为假,所以﹁p为真,即∀x∈R,有A=B≠∅,求此时a的范围。
解:(1)A⊆B。
理由如下:若A=∅,则A⊆B显然成立,这时集合A={x|f(x)=x},集合B={x|f[f(x)]=x};若A≠∅,设∀t∈A,则f(t)=t,f[f(t)]=t,即t∈B,从而A⊆B。
(2)因为p为假,所以﹁p为真,即∀x∈R,有A=B≠∅。
由(1)知A中的元素满足f(x)=x,即a x2-1=x。由A≠∅知a=0或
B中的元素是方程a(a x2-1)2-1=x,即a3x4-2a2x2-x+a-1=0的实根,由A⊆B⇒(a x2-x-1)(a2x2+a x-a+1)=0。
由A=B知方程a2x2+a x-a+1=0无实根,或其解是方程a x2-x-1=0的解。
若方程a2x2+a x-a+1=0无实根,则
若方程a2x2+a x-a+1=0有实根,可
小结:从定义出发分析解答题目是很基本的思路。对A=B的理解,选择从A⊆B(B⊆A)入手,再结合高次多项式分解的原理,就找到解决问题的突破口了,当然后续的讨论,层次要清晰,不能乱序。
例2 已知函数f(x)是奇函数,且在(-∞,+∞)上为单调函数,若实数x,y满足等式f(x2-2x)+f(y)=0,求2x+y-1的最大值。
分析:u=2x+y-1是一个二元变量函数,需要消元,根据条件得到x,y的关系,消去y,化为u关于x的一元函数即可求解。
解:因为f(x2-2x)+f(y)=0,所以f(x2-2x)=-f(y)。因为f(x)为奇函数,所以f(x2-2x)=f(-y)。又因为f(x)在(-∞,+∞)上单调,所以x2-2x=-y,所以u=2x+y-1=-(x-2)2+3≤
小结:利用单调性化简f(x2-2x)+f(y)=0得到x,y的关系式是问题解决的关键。回答最值,必须说明何时取得。
例3 已知f(x)=l o gax(a>0,a≠1),如果对于任意x∈[2,+∞)都有|f(x)|≥1成立,试求实数a的取值范围。
分析:可以优先考虑去绝对值,也可以先考虑不等式恒成立,进行变量分离。
解:由条件|f(x)|≥1⇒|l o gax |≥1⇒≥|l o g2a|(g(x)=|l o g2x|)。
第五个支出是社会保障支出,关于社会保障支出的主要有以下几个问题:社会保障支出总量不足;社会保障支出增长缓慢;社会保障支出结构不合理、地区差异显著;社会保障基金增值困难、安全隐患。这个具体的数据大概说一下:2010年的时候我们国家社会保障支出占GDP的2.28%。这个与同期国家比较,比如说以中等发达国家为例,中等发达国家社会保障支出比重是30%,我们是2.28%,社会保障构建上严重投入不足,今天我们所讲的全民享有的、能够覆盖13亿人口的社会保障体系尚未完全建立起来。
因为g(x)=|l o g2x|(x≥2),所以g(x)min=1,所以|l o g2a|≤1且l o g2a≠0⇒1<a≤2。
小结:变量分离是解决不等式恒成立问题的首选方法,此法能将不等式恒成立问题很快转化为函数最值问题加以解决。利用对数换底公式拆分出l o g2a是不错的运算技巧。
四、跟踪练习
审题分析:由于函数关系式是以根式的形式来表达的,利用导数求解不便。利用复合函数的单调性法则,需要考虑先求定义域D,且使(-4,2-a)⊆D。
综上,a的取值范围是[4,6)。
A.(0,1) B.(0,1)∪(2,+∞)
C.(0,1)∪(2,+∞)
D.(0,2)∪(2,+∞)
审题分析:由于初等函数的连续性,f(x)没有零点,可以考虑其有界性,用最值加以描述。
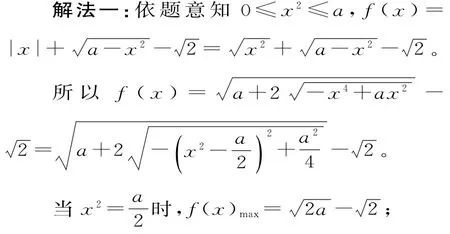
当x2=0时,f(x)min=a-2。
解法二:(换元法)因为x2≤a,所以可设

