导数、定积分知识结构与拓展
■河南省信阳高级中学 熊成兵
一、知识结构框架

二、结构分析
微积分的创立是数学发展中的里程碑,它的发展和广泛应用开创了向近代数学过渡的新时期,为研究变量和函数提供了重要的方法和手段。导数、定积分都是微积分的核心概念。在本章中,要理解导数的概念,了解导数在研究函数的单调性、极值与最值、零点问题,以及导数与不等关系中的作用,感受导数在解决实际问题中的作用,了解微积分的文化价值。本部分一直是高考的重点和难点。一般以基本初等函数为载体,利用导数研究函数的性质;利用导数解决与不等式相关问题;本部分涉及的数学思想主要为分类整合思想,转化与化归思想,对同学们的运算求解能力和推理论证能力的提高有很大的帮助。
三、实例分析
例1 设函数f(x)=x3+(a-1)x2+a x,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( )。
A.y=-2x B.y=-x
C.y=2x D.y=x
分析:本题考查函数的对称性和导数的几何意义及其运算。利用奇函数偶次项系数为零求得a=1,进而得到f(x)的解析式,再对f(x)求导得出切线的斜率k,进而求得切线方程。
解:因为函数f(x)是奇函数,所以a-1=0,解得a=1,所以f(x)=x3+x,所以f'(x)=3x2+1,所以f'(0)=1,f(0)=0,所以曲线y=f(x)在点(0,0)处的切线方程为y-f(0)=f'(0)x,化简得y=x。故选D。
小结:该题考查的是有关曲线y=f(x)在某个点(x0,f(x0))处的切线方程问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论:在多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,然后利用求导公式求得f'(x),借助于导数的几何意义,结合直线方程的点斜式求得结果。
例2 若函数f(x)=a x2+xl nx有两个极值点,则实数a的取值范围是( )。
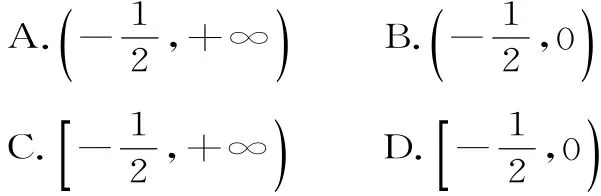
分析:本题利用导数研究零点问题。求导,将函数有两个极值点转化为导函数有两个不同的正零点,再求导,将函数有零点转化为判定极值的符号。
解:因为函数f(x)=a x2+xl nx有两个极值点,所以g(x)=f'(x)=2a x+1+l nx=0有两个不同的正零点。因为g'(x)在(0,+∞)上恒成立,则g(x)在(0,+∞)上单调递增,g(x)=0不可能有两个正根(舍)。
小结:(1)研究函数问题要注意“定义域优先原则”,否则会出现增根,从而导致出错;
(2)利用导数研究函数存在极值问题时,要注意转化为其导函数有两个不同的零点,而判定函数的零点的个数,往往转化为判定函数的单调性和极值的符号。
例3 设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f'(x)c o sx-
A.a<b<c B.b<c<a
C.c<b<a D.c<a<b
分析:构造函数g(x)=c o sx·f(x),求导,通过判定导数的符号确定函数的单调性,再进行比较大小。
解:令g(x)=c o sx·f(x),因f'(x)·c o sx-f(x)s i nx>0在(0,π)上恒成立,所以g'(x)=f'(x)c o sx-f(x)s i nx>0在(0,π)上恒成立,即g(x)在(0,π)上单调递增,则
小结:本题利用导数研究函数的单调性,解决本题的难点在于结合“f'(x)c o sxf(x)s i nx>0 在(0,π)上 恒 成 立”和这需要学生对导数公式及其结构非常熟练。
例4 已知函数f(x)=2 s i nx+s i n2x,则f(x)的最小值是____。
解:f'(x)=2 c o sx+2 c o s2x=4 c o s2x时函数单调增,从而得到函数的减区间为
小结:该题考查的是有关应用导数研究函数的最小值问题,在求解的过程中,需要明确相关函数的求导公式,需要明白导数的符号与函数的单调性的关系,确定出函数的单调增区间和单调减区间,进而求得函数的最小值点,从而求得相应的三角函数值,代入求得函数的最小值。

分析:(1)首先确定函数的定义域,然后对函数求导,再对a进行分类讨论,从而确定出导数在相应区间上的符号,最终求得函数对应的单调区间;(2)根据f(x)存在两个极值点,结合第(1)问的结论,可以确定a>2,令f'(x)=0,得到两个极值点x1,x2是方程x2-a x+1=0的两个不等的正实根,利用韦达定理将其转换,构造新函数并利用其单调性证得结果。

①若a≤2,则f'(x)≤0,当且仅当a=2,x=1时f'(x)=0,所以f(x)在(0,+∞)上单调递减。
(2)由(1)知,当且仅当a>2,f(x)存在两个极值点。
由于f(x)的两个极值点x1,x2满足x2-a x+1=0,则x1x2=1,不妨设x1<x2,
小结:该题考查的是应用导数研究函数和不等式问题,涉及的知识点有应用导数研究函数的单调性、应用导数研究函数的极值问题,在解题的过程中,需要明确导数的符号对单调性的作用,确定函数的定义域,对参数进行讨论,并构造新函数来解决问题。
四、跟踪练习
1.若函数f(x)=2x3-a x2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[-1,1]上的最大值与最小值的和为____。
解析:由f'(x)=6x2-2a x=0得x=为函数f(x)在(0,+∞)上有且仅有一个零点且f(0)=1,所得a=3。从而函数f(x)在[-1,0]上单调递增,在[0,1]上单调递减,所以f(x)max=f(0),f(x)min=m i n{f(-1),f(1)}=f(-1),所以f(x)max+f(x)min=f(0)+f(-1)=1-4=-3。
小结:对于函数零点个数问题,可利用函数的单调性、草图确定其中参数取值条件。从图像的最高点、最低点,分析函数的最值、极值;从图像的对称性,分析函数的奇偶性;从图像的走向趋势,分析函数的单调性、周期性等。
2.如图1所示的阴影部分是由x轴,直线x=1及曲线y=ex-1围成,现向矩形区域O A B C内随机投掷一点,则该点落在阴影部分的概率是( )。

图1

小结:定积分应用。先由定积分求出阴影部分面积,再利用几何概型即可求出点落在阴影部分的概率。

