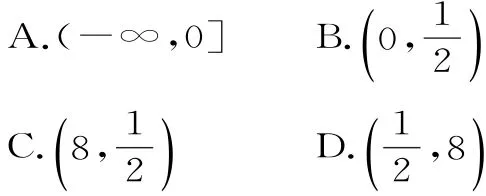高中数学创新试题的探索

■河南省信阳高级中学 李楠楠

高中数学创新题是指根据数学课程标准的理念和要求,依托一定的数学命题原理和技术,旨在培养或诊断同学们的数学创新意识与创新能力,在题目背景、题目形式、题目内容、解题方法等方面具有一定的新颖性与独特性的数学题。

一、定义新

纵观全国各地高考试卷中的创新题,不难发现,“新定义”型题目是创新题型的新宠儿。“新定义”主要包括定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解。

1.新概念。

例1 用C(A)表示非空集合A中元素的个数,定义 A*B=2},B={x|(x2+a x)·(x2+a x+2)=0},且A*B=1,设实数a的所有可能取值组成的集合是S,则C(S)等于( )。

A.1 B.3 C.5 D.7

解析：由已知可得(x2+a x)·(x2+a x+2)=0等价于x2+a x=0 ①,或x2+a x+2=0 ②。

因为A={1,2},且A*B=1,所以集合B要么是单元素集合,要么是三元素集合。若集合B是单元素集合,则方程①有两个相等的实数根,方程②无实数根,所以a=0;若集合B是三元素集合,则方程①有两个不相等的实数根,方程②有两个相等且异于方程±2 2。综上所述,a=0或a=±2 2,所以C(S)=3。故选B。

2.新运算。

A.m i n{|a+b|,|a-b|}≤m i n{|a|,|b|}

B.m i n{|a+b|,|a-b|}≥m i n{|a|,|b|}

C.m a x{|a+b|2,|a-b|2}≤|a|2+|b|2

D.m a x{|a+b|2,|a-b|2}≥|a|2+|b|2

解析：对于选项A,取a⊥b,根据勾股定理,可知结论不成立;

对于选项B,取a,b是非零的相等向量,则不等式左边m i n{|a+b|,|a-b|}=0,显然不等式不成立;

对于选项C,取a,b是非零的相等向量,则不等式左边m a x{|a+b|2,|a-b|2}=|a+b|2=4|a|2,而不等式右边=|a|2+|b|2=2|a|2,显然不成立。

由排除法可知,选项D正确。故选D。

3.新法则。

分析：根据所给的两个点的坐标写出直线方程,设出两个点的坐标,根据所给的映射对应法则得到两个点的坐标之间的关系,代入直线方程求出一个圆的方程,得到轨迹是一个圆弧,求出弧长。

解：根据题意可得直线A B的方程为x+y=4,设点 M(m,n),M'(x,y),则以M'的轨迹是一个圆弧,且

二、背景新

纵观全国高考试题,以高等数学为背景的创新试题备受命题专家青睐,是高考试题中一道亮丽的风景线。

例4 设S为复数集C的非空子集。若对任意x,y∈S,都有x+y,x-y,x y∈S,则称S为封闭集。下列命题:

①集合S={a+bi|(a,b为整数,i为虚数单位)}为封闭集;

②若S为封闭集,则一定有0∈S;

③封闭集一定是无限集;

④若S为封闭集,则满足S⊆T⊆C的任意集合T也是封闭集。

其中为真命题的是____(写出所有真命题的序号)。

解析：两个复数的和是复数,两个复数的差也是复数,所以集合S={a+bi|(a,b为整数,i为虚数单位)}为封闭集,①正确。当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确。对于集合S={0},显然满足所有条件,但S是有限集,③错误。取S={0},T={0,1},满足S⊆T⊆C,但由于0-1=-1不属于T,故T不是封闭集,④错误。故真命题是①②。

三、方法小结

创新题的题型新颖,形式多样,融综合性、应用性、开放性、创新性于一体。解题时要求认真理解题意,透过“现象”把握问题的“本质”,并将它抽象成数学(如集合、函数、数列、向量等)问题,运用相应的数学知识求解。解决这类问题通常分为三个步骤:(1)对新定义进行信息提取,确定解题的方向;(2)对新定义所提取的信息进行加工,探求解题方法;(3)对定义中提取的知识进行转换,有效地输出,进而解题。解决这类问题常见的思想与方法:直接法、特值法、排除法、数形结合、转化化归等。

四、巩固练习

A.奇函数 B.偶函数

C.既是奇函数又是偶函数

D.非奇、非偶函数

2.设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使得f(x0)=-x0,则称x0是f(x)的一个“次不动点”,也称f(x)在区间D上存在“次不动点”。若函数“次不动点”,则实数a的取值范围是( )。