f(x)=|g(x)-ax-b|的双重最值问题
■浙江省天台中学高三(1 5)班 王淑颖
函数是高中数学的一条主线,近几年的高考、学考、竞赛对绝对值函数的考查下足了功夫。下面笔者就形如f(x)=|g(x)-a x-b|这一类函数的最值问题提供一些基本方法,望能对读者有所帮助。
问题1 函数f(x)=|x-b|在[0,1]上的最大值为M(b),求M(b)的最小值。
解法2:(几何法)函数f(x)=|x-b|可看作函数y=x与y=b取相同自变量时函数值差的绝对值(纵向距离)。如图1,线段①代表函数f(x)=|x-b|在[0,1]上的最所以M(b)的最
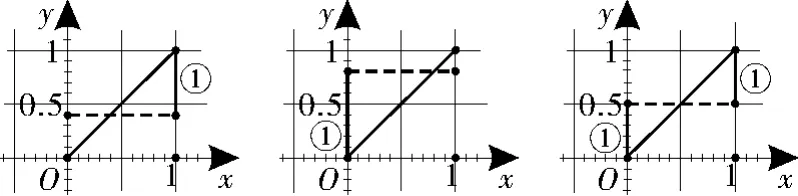
图1
问题2 函数f(x)=|x2-b|在[-2,2]上的最大值为M(b),求M(b)的最小值。
解析:如图2,线段②代表函数f(x)=|x2-b|在[-2,2]上的最大值为M(b),当b<2或b>2时,M(b)>2;当b=2时,M(b)=2。所以M(b)的最小值为2。

图2
问题3 函数f(x)=|2x-b|在[0,2]上的最大值为M(b),求M(b)的最小值。
解析:如图3,线段①代表函数f(x)=|2x-b|在[0,2]上的最大值为M(b),

图3
将问题1、2、3进行推广,可以得到如下结论:
结论1 已知函数f(x)=|g(x)-b|,g(x)是闭区间上的连续函数,记f(x)的最大值为M(b),则M(b)的最小值为
问题4 函数f(x)=|x2-a x-b|在[-2,2]上的最大值为M(a,b),求M(a,b)的最小值。
解析:函数f(x)=|x2-a x-b|可看作函数y=x2与y=a x+b取相同自变量时函数值差的绝对值(纵向距离)。由图4得,当a=0,b=2时,M(a,b)取得最小值2。
问题5 函数f(x)=|x2-a x-b|在[0 ,2]上的最大值为M(a,b),求M(a,b)的最小值。
解析:(1)连线,连接O B,记直线l1,此时l1:y=2x;

图4
(2)作平行切线,切点为A(1,1),此时切线l2:y=2x-1;
(3)取中间线,直线l到直线l1和l2距离相等,此时中间

图5
结论2 已知函数y=g(x)是闭区间上的凸函数(或凹函数),且y=g(x)的图像被两条平行线y=k x+b1和y=k x+b2(一条直线过曲线两端点,另一条是平行切线)完全“夹死”,记函数f(x)=|g(x)-a x-b|的最大值为M(a,b),则
解析:如图6,易知,直线A B:y=-x+3,平行切线l2:y=-x+2 2,所以M(a,b)的最小值为

图6
巩固练习:
1.若对任意x∈ [- 1,1],恒有|4x3-a x|≤b,则当b取得最小值时,a的值为____。
答案:3
2.已知函数f(x)=|c o s2x+as i nx|的最大值为b(a≤0,b∈R),则a+b的取值范围是____。
答案:[0,1]

