泥沙运动统计理论前沿研究成果

韩其为

（中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038）

1 研究背景

泥沙运动统计理论是指利用流体力学、河流动力学及概率论、随机过程相结合的途径来深入研究泥沙运动。最早在推移质扩散中引进概率论方法的是A.H.Einstein［1］，他研究了沙子在水槽中沿程和随时间的扩散，得到了分布函数，但由于两个参数无法确定，加之未与泥沙运动热点——起动与推移质联系起来，在欧美30年内未引起反响。后来放射性示踪技术的发展，结合试验，该扩散问题才被重新研究［2］，但始终未越出Einstein的框框而逐渐停滞。由于没有和力学及泥沙运动联系起来，而且开辟的研究内容太窄，始终缺乏推动力。后来Einstein［3］做了根本改变，初步采用了力学与概率论相结合的方法，但他是以力学方法为主研究推移质运动，给出的结果中，除提出交换外，仅引进了起动概率。他这次的成果却引起了强烈反响，到目前为止仍有跟随研究，其影响长期不衰。这不仅得益于采用了力学与概率论相结合的方式，而且抓住了泥沙运动与工程泥沙所关心的问题。之后，欧美、日本及前苏联也沿着这个方向进行，成了1950年代以后泥沙运动理论研究的主流。不足的是，研究内容仍基本限于泥沙跳跃、推移质输沙率及推移质扩散分布。可见，从国外研究情况看，由于范围窄，深度浅，力学与概率论相结合的研究方式还远达不到泥沙运动统计理论，只能算为它的起步。

我国学者起步也早，窦国仁［4］1965年即发表了推移质跳跃运动及输沙率的理论研究。韩其为［2］1984年也开始了利用概率论随机过程与力学相结合的方式开展长期深入研究。孙志林［5］也开始了这方面的某些研究。尚需说明的是，近10多年来国外也有利用随机过程研究泥沙运动的极少数论文，但是仅针对输沙率，而且多限于推移质，并且还要借助于经验成果，故暂不提及。前后经过50余年的不断深入研究，本项目已建立了泥沙运动统计理论体系，不仅单独研究了一些课题，而且涉及到目前已有的泥沙运动理论的补充、提升和改造，同时开辟了很多新的领域，完成了大量创新，使泥沙运动统计理论成为泥沙运动的一个分支。下面对这项成果的主要部分予以介绍。

2 泥沙运动统计理论前沿研究成果

2.1 泥沙运动的概化图形［2，6-7］泥沙运动共有4种状态：静止、滚动（滑动）、跳跃与悬浮。前3种运动的泥沙集中在床面层（跳跃高以下），悬移常常冲出床面层，上升至悬浮高ym≤H。这4种运动在确定条件下满足力学方程。在条件不确定时，它们的运动是随机的。影响颗粒运动随机有3个方面：底部水流速度（纵向底速Vb、竖向底速Vb.y）、颗粒在床面位置（暴露度）Δ′以及泥沙级配Pl。底速的分布为正态分布，Δ为均匀分布（对于均匀沙）或不均匀分布，级配为已知的经验分布。当这三方面的随机变量取确定值，则运动满足相应的力学方程，是确定的；否则是随机的，但是可以求出其数学期望。

2.2 单颗泥沙运动力学及统计规律［2-9］

（1）3种运动泥沙（滚、跳、悬）统一的升降过程。泥沙由床面起动后，上升一定的高度（跳跃高或悬浮高）或完成一个起动过程（滚动），则开始下降，直至床面。在上升至最高点后下降至床面的两个床面接触点之间的运动称为一个单步，两个在床面停留点之间的运动称为一个单次。单次运动由若干单步运动组成。

（2）对滚动又分为前半步（接触滚动）和后半步（自由运动）。建立了前半步滚动的5种力学方程和后半步的1种方程。已求出它们的分析解和有关运动参数以及数学期望。对滚动的研究，过去几乎是空白，本研究予以填补。

（3）跳跃运动力学及统计规律。①研究了碰撞后产生的速度方程，从理论上证实了未得到共识的离散力，这里予以澄清。②建立了竖向运动第1阶段3种情况的3种方程，第2阶段、第3阶段各一种方程，纵向运动1种方程，求出了这些方程的分析解，以及有关脱离床面时间、跳跃高度、长度和速度等数学期望。并用一些试验资料进行了验证。在已有的跳跃研究中多为抓住一个环节进行，本项研究则将这些研究联系进行，得到了跳跃全过程较为完整统一的理论结果。

（4）悬浮颗粒运动涉及到一系列参数，包括上升与下降速度、水流的作用流量、流速分布与含沙量分布和跳跃高及其分布等等。特别是其中的跳跃高度是一个全新的概念，它与含沙量分布一一对应。而颗粒脱离床面时间与紊动猝发周期有关。

2.3 床面泥沙交换强度［9-12］

（1）提出了床面泥沙改变状态的基本概率，即起动概率ε0、止动概率1-ε0、由静起跳概率ε2.0、由动起跳概率ε2、悬浮概率ε4和起悬概率 β，以及由这6种基本概率推出的其他10种概率，而组成4×4方阵，即转移概率矩阵，见式（1）。

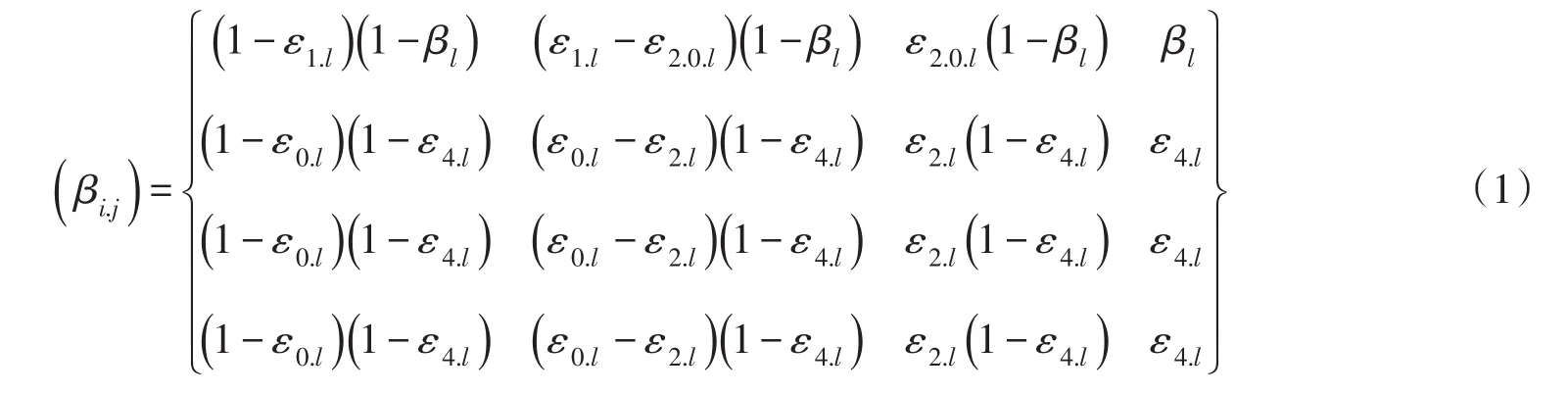
（2）对于马尔科夫链，上述转移矩阵能完全确定其随机特性，从而得到泥沙在床面4种状态的状态概率（见表1）。

（3）床面泥沙交换强度。如果进一步考虑泥沙在维持一种状态需要一定的时间，则可得到泥沙交换的16种交换强度。其中4种是维持原状态的强度。而其余12种是不同状态之间的交换转移强度。

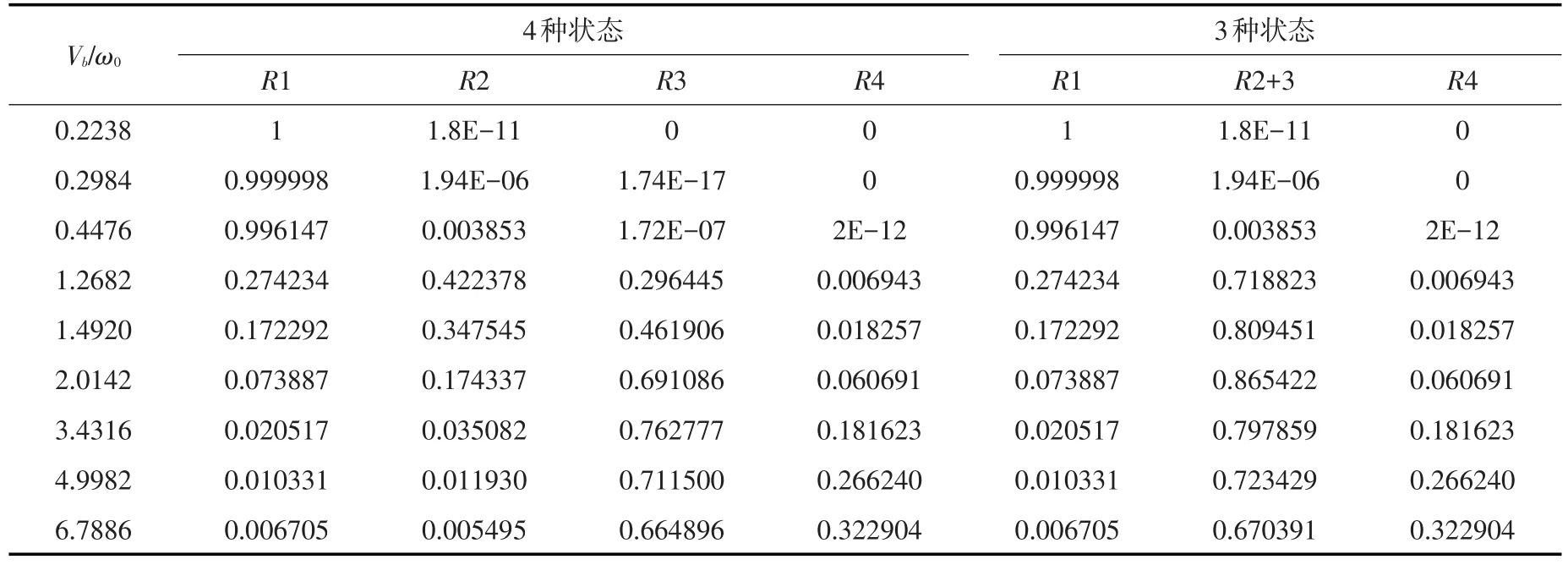
表1 状态概率的数字结果

2.4 多种输沙能力揭示及表达［10-13］

（1）由交换强度中的λ1.3.l=λ3.1.l可简单的导出推移质跳跃输沙率，它可以涵盖数种推移质输沙率公式，包括最著名、影响最大的A.H.Einstein公式。而且由交换强度还可导出滚动输沙率公式，包括滚动加跳跃的推移质输沙率公式，以及它们的比值。

（2）由与悬浮有关的参数，包括λ1.4.l及λ4.1.l共有27个公式和参数组成，求解后可得出新的强平衡条件下挟沙能力公式。它是目前考虑因素最多、机理阐述最清楚的挟沙能力公式。与大量实际资料符合较好，并且在一定范围内能概括目前国内流行的张瑞瑾公式、维里卡诺夫公式以及韩其为以前在数学模型中使用的两个公式。特别是对目前最有名、最权威的Einstein挟沙能力公式，能从理论上全面修正，包括上举力正态分布改为底部流速的正态分布；推移质单步长度不是L=100D；底部悬移质含沙量并不等于推移质平均含沙量，而它们的比值是变化的；推移质跳跃高不是2D；推移质与床沙交换的时间不是，而决定于起动周期，或紊流猝发周期。笔者不仅吸收他思路的正确部分，而且较早（1984年）地指出了他研究的不足和问题，并给出了正确的代替。

（3）上述按λ1.4.l=λ4.1.l研究悬移质与床沙交换的挟沙能力，是属于强平衡，即两种状态之间达到平衡。其实得到4种状态之间的12种交换强度，不仅有多种两两之间的平衡，还有4种状态之间的弱平衡，即4种状态之间的总体平衡。如悬移质与床沙、滚动和跳跃之间总体达到平衡，即：

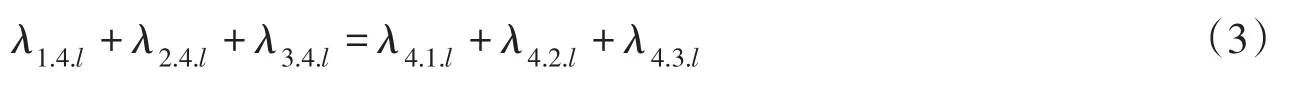
或者将交换强度代入，有：

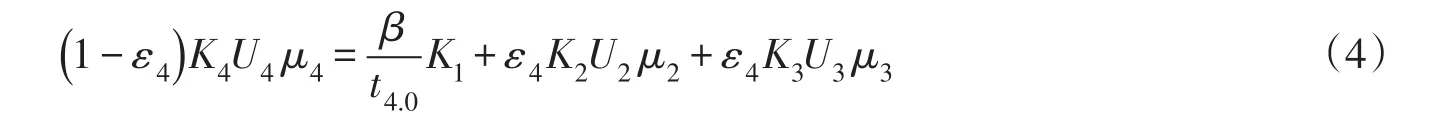
再将一些参数的表达式代入，得到悬移质与其它3种状态弱平衡交换时的输沙能力为：

当然，若悬移质与其它3种状态之间强平衡交换，则有λ1.4.l=λ4.1.l等，即：

此处m0=0.4，γs为泥沙容重，φ4为悬浮运动综合概率。而上述两式均是对均匀沙举例，对非均匀沙也有类似的结果，只是加一粒径组标号，则公式变为分组的。

（4）过去的研究只认为有两种输沙能力——推移质输沙能力和悬移质输沙能力。从上述研究看，这种看法是很局限的，由12种交换强度可导出9种输沙能力。可见，交换强度能广泛、深刻地揭示输沙能力，大大开阔了眼界。同时表明交换强度是最基本的。

2.5 泥沙起动规律及起动流速［14-16］

（1）引进Van der Walls力导出了颗粒间黏着力，同时给出了薄膜水附加下压力的表达式，从而由理论上建立了泥沙瞬时起动底部流速方程。

（2）建立了起动随机模型，证实了在起动阶段单步距离及起动周期符合指数分布，导出了起动流速分布以及它的数学期望，从而得到平均起动流速公式。

（3）指出瞬时起动速度是确定的，而时均起动速度是不确定的。进而定义了方便识别的起动标准，即相对输沙率λk，使起动流速观测和计算能定量进行。

（4）首次从理论上引入干容重，使起动流速公式适用于不同密实程度。

（5）本项研究着眼于泥沙起动规律，研究颇为深刻，是理论性最强的成果。澄清了没有公认起动标准条件下，不同观测者成果为何能集中在一条拟合线上。

2.6 床面泥沙边界条件［17］

（1）床面泥沙边界条件是泥沙运动、尤其是求解扩散方程主要定解条件之一，因为它决定了冲淤。多年来，不同学者先后提出了6种，笔者曾在文献［1-19］中对现有的前5种进行了讨论。它们大多是经验的或半经验的，有的虽然有一些定量的分析，但是其中的参数是经验的。有的给出的边界条件甚至是不合理或矛盾的。没有一个公式是由较严格的理论导出的。

（2）根据床面泥沙交换统计理论，很容易导出床面边界条件

式中，等号左边为扩散方程边界条件；中间为床面泥沙交换强度；右边为恢复饱和系数αl*、，以及由平均挟沙能力与平均含沙量之差表示的冲淤量。

（3）上述边界条件对一维就是其不平衡输沙方程，对立面二维和平面二维则是边界条件。上述方程是笔者首次提出（1973年）。但是有的作者对上式的写法，往往不严格，以致误解。例如，有的写成 αωlP4.l(S*-S)，有的写成αωl(P4.l*S*-P4.lS )。笔者最早也曾采用过它们作为近似。前者隐含了各组粒径冲淤同号；后者给出了冲淤恢复速度相同，排除了挟沙能力多值性。

2.7 一维悬移质不平衡输沙模型研究［18-22］目前二维、三维水沙数学模型较为广泛流行，因此有的对一维数学模型有所轻看。其实，一维水沙数学模型的可靠性在于泥沙部分的计算是否可靠，是否详尽。从这一点出发，在1970年代，笔者提出了一个一维泥沙数学模型，它不仅可以求不平衡输沙条件下含沙量、悬移质级配、床沙冲淤及级配的耦合解，而且后来又使用了前述边界条件。该模型在国内外是最先进的。此模型包含了含沙量及挟沙能力沿程变化，含沙量级配的沿程变化，冲淤条件床沙级配的变化。先后经过20余个天然河道、水库、水库下游河道及回淤区冲淤资料多方面的检验，证明符合实际。该模型自1970年代末开始在三峡工程论证、设计以及试运行和正常运行各阶段应用，在考虑上游来沙减少后是符合实际的。同时该模型已在金沙江下游、长江中下游、以及稍加补充后在黄河中下游及三门峡、小浪底水库、塔里木河和淮河等广泛使用。

2.8 推移质不平衡输沙研究［7，10］推移质与床沙和悬沙同时交换时不平衡输沙公式

推移质与床沙交换的不平衡输沙公式

推移质与悬移质交换的不平衡输沙公式

2.9 床沙粗化研究［7，23］床沙粗化是一个较早研究的课题，但是大都偏重于经验和半经验，缺乏深刻的理论描述。笔者曾收集了不同粗细床沙和不同宽窄范围床沙粗化的6种形式。按这些现象用床面泥沙交换强度，床沙粗化机理及根据就非常清楚。如推移质冲刷粗化可由λ1.b.l-λb.1.l来描述，悬移质冲刷粗化可由λ1.4.l-λ4.1.l表达。当然如果同时考虑两种粗化，则是它们叠加。在一定简化后可以导出这两种粗化时床沙级配变化公式。图1为丹江口水库下游汉江黄家港至光化河段卵石挟沙级配（属于宽级配）粗化过程。

推移质冲刷粗化与悬移质冲刷粗化的差别见图2。图2表明，沙质河床粗化主要靠悬移质冲刷，而不是推移质冲刷。

图1 床沙级配粗化过程（汉江黄家港-光化河段）

图2 粗化层级配对比

与冲刷粗化并行，尚存在后面提到的交换粗化，已导出了其方程。

2.10 推移质扩散新的研究及突破［24］笔者补充了点源扩散中的初始状态为运动的输移分布，使点源条件下，4种分布全部给出。

系统处理了点源、线源、退化面源不同的扩散，还包括固定参数与变动参数，忽略运动时间与考虑运动时间，统一导出了它们的分布函数。

扩散模型的研究面很窄，基本仅限于点源，仅文献［11］涉及到线源，研究的重点是导出假定条件少的更一般的分布函数。这种研究难以与工程泥沙问题联系起来，缺乏推动力。将点源扩大为线源，就能与河流泥沙相联。如从初始时刻加一P0(t)分布于源点，则构造一个线源，可研究其在0—x河段的沉积分布。类似地，也可以在初始时刻加一P0(x)分布于河段，研究它的输移分布。这样由点源扩散可构造8个线源扩散，而两个线源构造一个退化面源扩散。共研究了4种退化面源扩散（包括初始状态为静止和运动的沉积分布与输移分布），得到了分布密度及分布函数。

此项研究完善了点源扩散，深入研究了线源和面源扩散，得到了其分布，特别是突破了多年来扩散研究不考虑运动时间的难题。

3 开辟了新的研究领域

3.1 挟沙能力级配及有效床沙级配研究［25-27］

（1）笔者首次引进的挟沙能力级配及有效床沙级配［25］，它们是非均匀沙不平衡输沙的重要组成部分，也是一种有效的工具。对于不平衡输沙，挟沙能力级配不能采用P4.l，床沙级配不能采用P1.l.1，并且利用引进的挟沙能力级配及有效床沙级配可以将均匀沙的有关成果转化为非均匀沙的。

（2）对非均匀沙，挟沙能力级配及有效床沙级配可以证明有10条特性。包括：

（3）断面挟沙能力级配及有效床沙级配的一般表达式：

（4）几种特殊条件下挟沙能力级配及有效床沙级配。共有4种情况，包括来沙全部转为挟沙能力，床沙全部可悬；来沙部分转为挟沙能力，床沙全部可悬；来沙全部转为挟沙能力，床沙部分可悬；以及来沙部分转为挟沙能力，床沙部分可悬。其中来沙全部转为挟沙能力，床沙全部可悬，则有：

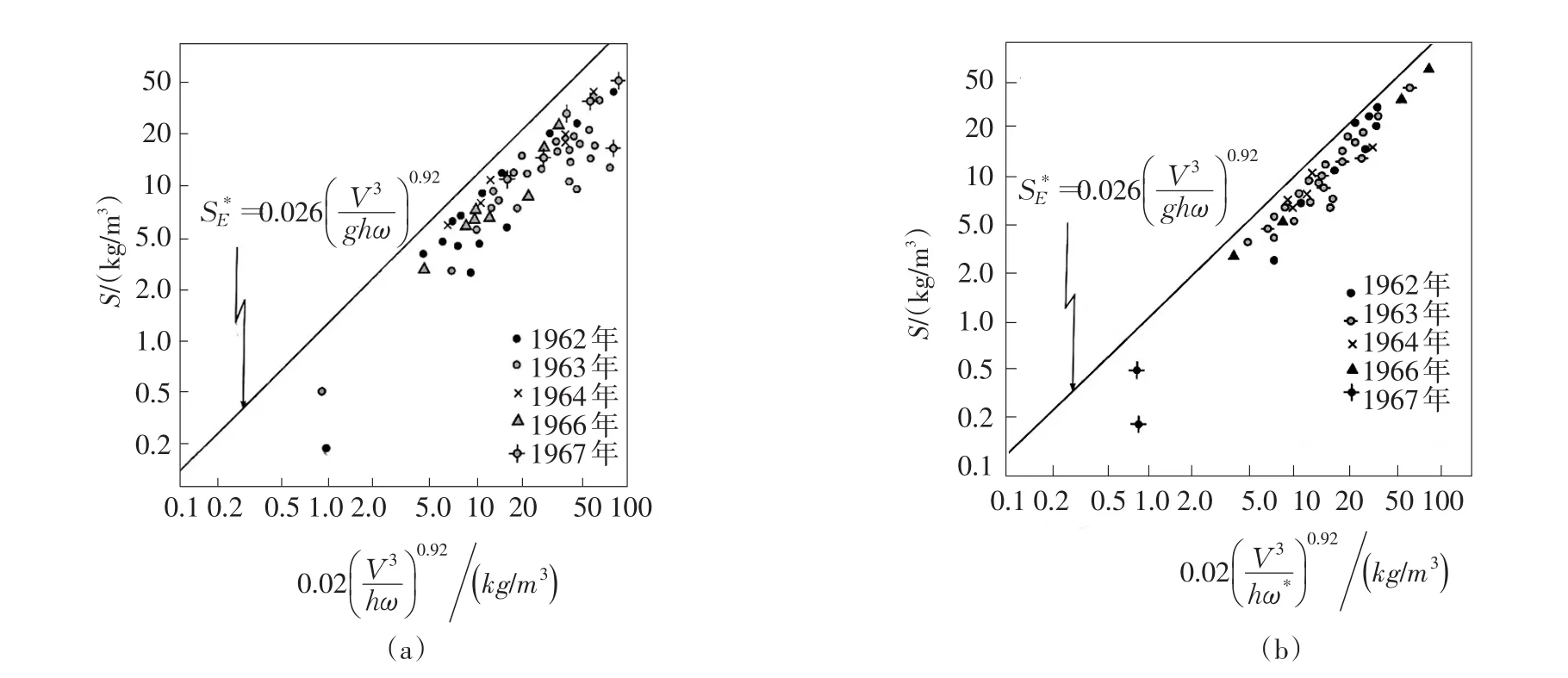
图3 黄河花园口站在冲刷过程中挟沙能力关系

（5）对水库下游河道，目前不少研究及数学模型仍采用含沙量级配代替挟沙能力级配，结果与实际资料差别很大（图3（a））。但是，按式（20）、式（21）计算，与实际资料符合较好（图3（b）），各点均集中，也反映了冲刷时挟沙能力略小于平衡线。在图4中，按分组泥沙点绘了结果不同粒径符合同样的挟沙能力关系，即其中以m、s、kg/m3为单位。这表明不仅证明而且统一了床沙质、冲泻质与全沙的挟沙能力规律。这为水库中挟沙能力研究，特别是数学模型采用全沙计算提出了理论支撑。同时为更一般的非均匀沙挟沙能力理论研究提供了基础。

图4 长江新厂水文站分组含沙量与水力因素关系

3.2 粗细泥沙交换机理及多方面影响［23，28］

（1）笔者曾在丹江口水库下游汉江发现了河床冲淤在大多数条件下都不是单向的（1980年）。这与目前泥沙研究和数学模型计算的单向冲淤（或者全部粒径冲，或者全部粒径淤）不一致。这显然是研究成果没有完全反映实际。在表2中列出了河道变形（黄河）、水库下游河道冲淤（黄河、汉江、长江）、水库变动回水区（丹江口水库）大量的冲淤资料，证实了冲淤是粗颗粒淤下，细颗粒冲起。泥沙冲淤分为三种：明显淤积—全部粒径均淤，至少不冲；明显冲刷—全部粒径均冲，至少不淤；以及微冲微淤。粗细泥沙交换应属于微冲微淤。

（2）研究三门峡水库对黄河下游冲刷时，有人利用二维扩散模型求解得到含沙量恢复距离为800 m。实际运行后，当流量在2500～3000 m3/s时，冲刷（含沙量恢复）不是800 m，而是直达河口，为800 km。有专家分析其原因是洪水漫滩后滩槽泥沙交换，引起的主槽含沙量减小而冲刷。但是这不能解释水流不上滩的情况。

（3）利用一维不平衡输沙方程及最一般的挟沙能力方程可以从理论上证明，粗细泥沙交换是完全能出现的。其实，明显淤积是水库淤积的一种极限；明显冲刷是水库溯源冲刷的一种极限。微冲微淤、粗细泥沙交换才是一般现象。

（4）假设水力因素（流速V及水深h）沿程不变，但是床沙沿程线性变细，现已证明，此时挟沙能力级配沿程线性变细，1ω*m沿程线性加大，总挟沙能力线性增加。同时，对细颗粒，P1.l.1＞P1.l.0，细沙增加；对粗颗粒，P1.l.1＜P1.l.0，粗颗粒减小。并且这种现象直至河口。

表2 不同河道河段冲淤量

（5）加大了挟沙能力，改变了冲淤数量。例如，表2中皇庄至仙桃1980—1984年，d≥0.25 mm的粗沙淤1292万t，d＜0.25 mm的细沙冲刷15 075万t。由于它们的沉速比故粗沙淤1292万t，能换取细沙冲刷1292×7.82=10102万t。可见，在交换条件下，河床共冲刷15075-1292=13783万t，而如果不交换则仅冲刷15075-10102=4973万t。另一个例子是皇庄至仙桃1974—1979年，d＜0.10 mm细沙冲刷2635万t；d≥0.10 mm粗沙淤积1775万t，粗细合计共冲刷860万t。两者的平均沉速之比可见，在交换条件下，共冲刷2635万t细颗粒；而如果不交换，淤下的1775万t粗颗粒会交换1775×18.1=32128万t细颗粒。可见，如果粗细颗粒不交换不发生粗颗粒淤积，则细颗粒淤积1775×18.1=32128万t，加上原有的细颗粒冲刷2635万t，则细颗粒淤积32128-2635=29493万t。可见粗细泥沙交换使河床淤积变成了河床冲刷。当然，这里未考虑水力因素变化，如果考虑，则冲淤变化不会那样大。但是对冲淤的影响则是不能否认的。

（6）粗细泥沙交换揭示了存在另一种粗化，即交换粗化。如表2，丹江口水库汉江下游河道1974年d＜0.25 mm泥沙冲刷905万t，d≥0.25 mm淤积152万t。冲淤抵消，合计净冲刷753万t。此时，床沙中细颗粒冲走905万t，粗颗粒152万t淤下，床沙显然发生了粗化。再如该表中丹江口水库变动回水区1980—1983年，d＜0.05 mm冲刷1701万t，d≥0.05 mm淤积4446万t，冲淤合计净淤2745万t。但是，此时床沙中细颗粒减少1701万t，粗颗粒增加4446万t，显然已发生了粗化。这是淤积条件下的粗化。第三个例子是该表中汉江皇庄至仙桃1977年d＜0.10 mm细颗粒冲刷204万t，d≥0.10mm粗颗粒淤积202万t，冲淤抵消接近平衡，可是床沙仍然发生了粗化。

（7）粗细泥沙交换的分界粒径Dk。利用非均匀沙与均匀沙挟沙能力关系，有

3.3 挟沙能力多值性［29-30］

（1）关于挟沙能力是单值的，还是多值的，到目前为止，是一个有争议的问题。有争议是指一种认为挟沙能力是单值的，另一种认为是多值的。两种看法各持一词，也会提出一些“证据”，但无法从理论上证明。所谓单值与多值的标准也没有统一的认识。这些正是长期存在争论的原因。但是这两种不同的看法影响很大，甚至会影响悬移质挟沙能力研究的发展方向。

（2）尽管到目前为止，认为挟沙能力是单值的看法在泥沙研究中占有多数，但是仍有一部分研究者认为是多值的，并且还是一些知名专家的看法和研究，如前苏联罗辛斯基和我国沙玉清、侯晖昌以及曹如轩等。张瑞瑾在其著名的挟沙能力公式的实测资料验证中，公式的上、下包络线，就是冲刷与淤积挟沙能力的范围。这说明他虽然没有提挟沙能力多值性，但是间接地呈现出它并不是单值的。需要指出的是，他们认为挟沙能力多值性的原因之一是临界速度多值性。如沙玉清根据资料分析，就提出了3种临界流速：开动流速、挟动流速和止动流速。侯晖昌认为挟沙能力是双值关系，并引用沙玉清临界速度进行了分析。曹如轩直接点了挟沙能力双值关系图。但他们均未从机理上具体分析和多值性直接推导。

（3）挟沙能力多值性的实际资料。表3给出了黄河下游河道历年平均资料，分3类列出：冲刷、平衡和淤积。这些资料是1960—1996年36年的平均。从表3中看出，无论冲淤还是平衡，挟沙能力包括进口挟沙能力S*及出口挟沙能力SL*是相近的，没有系统变化。但是，按此挟沙能力由不平衡输沙公式计算的含沙量与实际不符。需根据冲刷、平衡、淤积不同情况对挟沙能力进行修正，即分别乘以K=0.67、K=1.00、K=1.68改正挟沙能力后计算的含沙量，才能和实际的含沙量符合。这种冲刷时挟沙能力小于平衡的，淤积时大于平衡的，正是挟沙能力多值性的表现。

表3 黄河下游河道挟沙能力多值性

图5中用更多的资料证实了挟沙能力改正后计算含沙量与实测值符合很好。否则，如不改正（即按挟沙能力单值），则计算与实测差别很大。

（4）挟沙能力多值性的理论根据及机理分析。

①非均匀沙挟沙能力结构引起的挟沙能力多值性。它实际是由两部分组成：由上游输来已经含在水中的泥沙，以及由河床冲起的泥沙。前者的挟沙能力为S0*.l，后者为Sl.*0，后者与前者不一样，要受到黏着力与薄膜水附加下压力作用。这样，全部挟沙能力为

当 μl=1时，表示强平衡情况，挟沙能力全部由上游输来，于是

图5 取α=0.1修正挟沙能力多值性效果

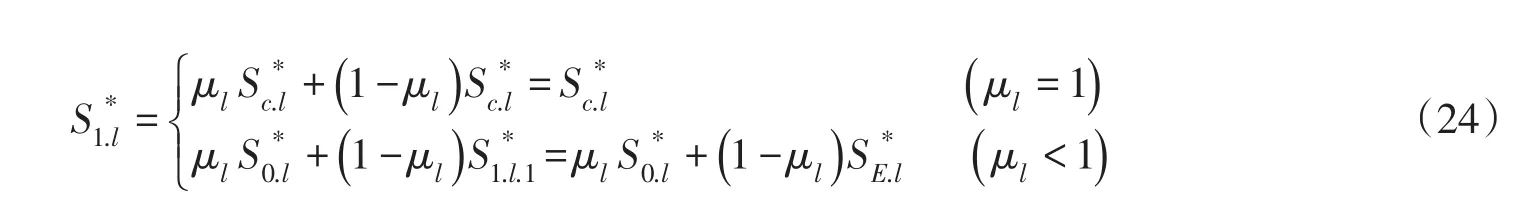
②恢复饱和系数引起的挟沙能力多值性。由不平衡输沙公式有：

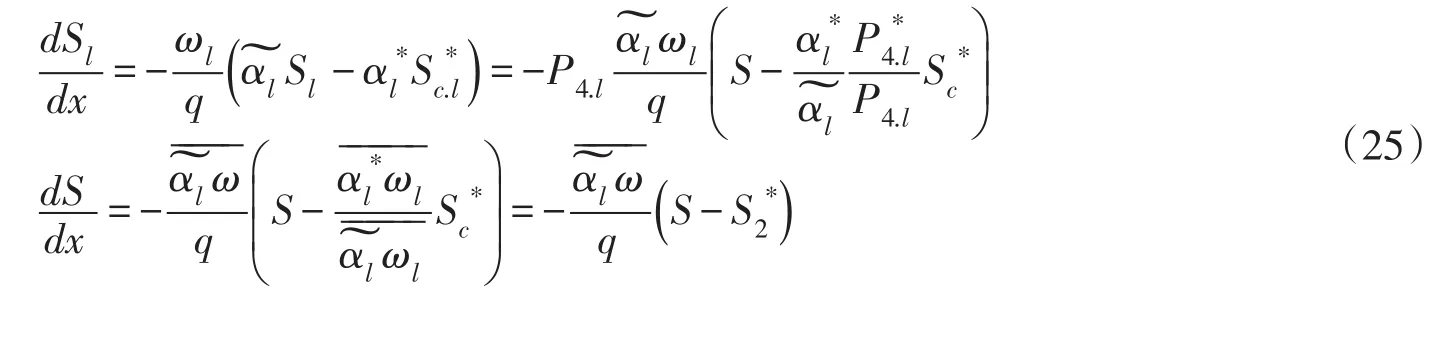
可见此时决定冲淤的不是S=S*，而是可称为虚挟沙能力。它实际起了挟沙能力的作用，正是挟沙能力多值性的表现。对于均匀沙，则有：

③挟沙能力结构与恢复饱和系数综合作用下的挟沙能力多值性。此时有：

（5）挟沙能力多值性的应用。已应用到黄河下游、淮河中游小柳巷以及三峡水库下游长江中下游河道。证实了挟沙能力多值性的存在，以及按本方法计算的结果基本符合实际。

3.4 黄河揭河底冲刷的理论研究［31］

（1）“揭河底”和“揭底冲刷”是黄河中游河道高含沙洪水时发生的一种强烈冲刷。此时，河底泥沙被成块掀起，而且还可以冲出水面。据水文年鉴描述“露出水面达数平方米，像是在河中竖起一道墙（与水流方向垂直）。二三分钟即落入水中消失”。据黄河龙门站发生揭底冲刷的资料为流速5.0～10.7 m/s，坡降7.2‰～31.8‰，水深约4 m左右。对于揭底冲刷已有一些研究，但均是经验的，没有从力学上对它的掀起、上升、冲出水面等进行理论分析。

（2）土块受力状态：正面推力FD，上举力FL，床面切应力τ0，土块水下重力G，底部床面薄膜水附加下压力∆G，底部颗粒间黏着力Fμ1，下游侧面黏着力转为向下的摩擦力Fμ2，两个侧面的黏着力转为向下的摩擦力。土块的几何形状abc取为a=b，扁度其中a为土块长和宽，c为厚。

（3）按照上述各力建立了土块起动的瞬时底速及时均底速公式，如瞬时起动底速公式为：

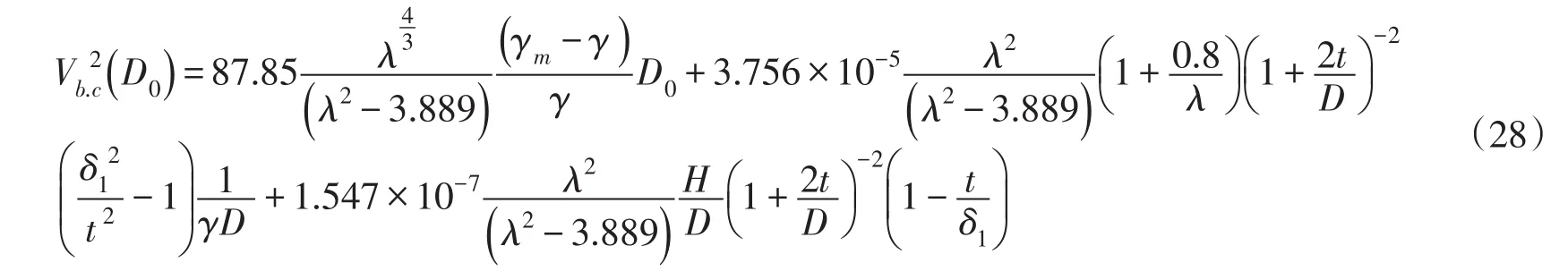
式中：γm为土块容重；γ为浑水容重；γ0为清水容重；D0为土块等容粒径；D为组成土块的单颗泥沙粒径。

经分析得到此时土块与单颗粒的受力有相当的变化。由于含沙量高，此时重力有很大减少。例如当含沙量达到600 kg/m3时，土块水下重力仅为单颗的更主要的是由于薄膜水附加下压力及黏着力均只是作用在土块几个面上，而不作用在土块的全部颗粒上，这两种力较之它们作用在全部颗粒上的值大为减少，仅占千分之一以下，实际可以忽略。

（4）土块的薄膜水附加下压力较之单颗的可以忽略，从而解释了泥沙研究中考虑单向受压与水深有关，和土力学中的超静水压力与水深无关的矛盾。这点是非常重要的澄清。

（5）经过一系列推导，得到土块时均起动流速为：

这是忽略薄膜水附加下压力和黏着力公式，故不再包含单颗粒径D。

（7）据时均起动流速公式，土块扁度系数λ愈大，起动流速愈小。如λ=10较之λ=4，起动流速减小0.477。这证实了“揭河底”的土块为什么是扁的，并且像帆一样。当然这与泥沙分层沉积有一定关系。

（8）由于忽略薄膜水附加下压力及黏着力，且水下重力大幅减弱，故此时很大土块也能起动。事实上，当S=900 kg/m3，H=4 m，D0=1 m（a=1.737，c=0.1737），平均流速2.32 m/s，即能起动。同样条件下，当D0=3 m（a=5.21 m，c=0.521），则V=3.42 m/s，即能起动。

（9）土块起动时，是以转动（向下游）形式进行。颗粒的转动方程是在正面推力力矩m(FD)、升力力矩my(FL)、阻力力矩my(R ) 及水下重力矩m(FG)和质量及附加质量的转动惯量作用下的运动。已建立了转动的较为复杂的一个方程。

（10）根据颗粒在床面转动方程的数字解，发现在θ=74°法向反力为负，开始脱离床面。另一方面，当θ=45∘时，uy.0最大，也可能直接上升而脱离床面。这表明，已证实土块起动时不一定到最高点θ=90°才脱离床面。

（11）土块上升及下降。土块上浮与下降运动从机理分析，仍然是一种推移质跳跃运动。即从床面至一个颗粒高（对于土块为a），接着继续上升，至最高点，再下降直至床面。建立了这3个阶段土块运动方程，包括它们的运动距离、速度和时间的方程，并且还考虑了加速与减速的不同情况。除上述竖向运动外，还建立了纵向运动方程。对这些方程均求出了分析解及数学期望。为了使大家有一印象，现举一个例子。设γm=1.839 t/m3，γ=1.374 t/m3，a=0.8 m，CL=1.2，Vˉ=7.27m/s，H=4 m，Vy=2.198 m/s，ux.0=1.873 m/s，从而得到土块上升全部时间t3=6.538 s，下降至床面的纵向平均速度7.12 m/s＜Vˉ=7.27 m/s，顺水流移动距离44 m。

（12）土块可能冲出水面。当土块上升至水面仍有一定速度时就会冲出水面。此时重力是变化的，已建立了其方程，得到了冲出水面的计算方法。例如当Vy=2.5 m/s，uy.c=1.147 m/s，土块露出水面的高度达到0.892 m，超过了它的长度0.8 m，即它已脱离水面。

4 焦点、难点的突破和争议的澄清

前面对泥沙运动统计理论从总体和其带动的研究领域成果进行了简要介绍。以下对研究中的焦点、难点的突破，创新点的建立以及争议的澄清进行了补充说明。

（1）首次证实了床沙质与冲泻质有共同挟沙能力规律（图5），并且均满足这不仅解决了长期存在不能计算的一个难点，也对数学模型计算中采用全沙给出了理论支持。

（2）突破了以往半经验、经验的方法，从理论上建立了床面边界条件，解决了不平衡输沙的一个焦点问题。

（3）最早用资料揭示并用理论证实了床面粗细泥沙交换是一般条件下河床沿程冲刷的基本形式，突破了河床演变总是单向冲淤（或冲或淤）的习惯看法。并据此给出了水库下游河道冲刷距离很长的原因。

（4）从理论上证实了泥沙成团起动流速可以小于组成该沙团的单颗泥沙的起动流速。例如，当D=0.005 mm，D0=0.0127 mm，当H=0.5 m，单颗起动流速为0.591，成团起动流速为0.703。但是当H=8 m，则单颗起动流速为1.781，成团起动流速为1.42，即成团小于单颗，以成团起动为主。

（5）多年来无法理解“揭河底”的动力来源得到揭示，除已知水力作用强、重力减弱外，证实了薄膜水附加下压力和黏着力大幅减小（转为内力）以至消失，是其主要原因。

（6）对于细颗粒的薄膜水单向压力转变导致与水深有关，而土力学中饱水土超静水压力与水深无关的矛盾，是宏观与细观的差别引起，从而排除了争议。

（7）统一了泥沙起动流速与输沙率，指出瞬时起动流速是确定的，时均流速是不确定的，从而提出了时均起动流速的约定标准（Vb.c及λqc），使时均起动流速能定量确定。在笔者之前，也有人提出几种起动标准，但方法不具体，难以应用。

（9）多年来认为床沙粗化是冲刷引起，研究方法也是建立在河床冲刷基础上，笔者首次研究了交换粗化，澄清了这个限制，并且给出了交换粗化方程。

（10）多种输沙率的揭示，突破了两种输沙率（推移质和悬移质）的长期制约，促进了研究。

（11）罗辛斯基提出的相加分组推移质的公式qb=∑Pb.lqb(l)，此式错误，应为qb=∑P1.lqb(l)，予以澄清。

（12）统一了粗细泥沙交换分界粒径与床沙质与冲泻质分界粒径，并给出了计算方法。而且这种分界粒径与挟沙能力级配也是一致的。

（13）首次从理论上得到了输沙率分布为Erlang分布，当n→∞，它趋近泊松分布。已经用试验资料检验了这种分布，与实际颇为符合。

（14）非均匀沙不同的混合方法对干容重有相当的影响。干容重的大小，决定于颗粒间间距t，从而决定单颗泥沙黏着力及薄膜水附加下压力。同时干容重还影响颗粒成团起动流速。笔者首次引入了不同粒径之间的接触概率，从而能根据混合沙的级配，采用随机充填得出干容重。