积累数学活动经验 发展学生数学素养

顾大权，姚楚舒

（江苏省张家港市第一中学）

数学基本活动经验是个体在亲身经历数学活动过程中所获得的关于数学活动的个性化经验.《义务教育数学课程标准（2011年版）》中将课程目标由“双基”改为“四基”，增加了数学基本思想和基本活动经验.数学活动经验从不同的角度，可以有不同的分类.按照前苏联数学教育家斯托里亚尔的学习活动阶段划分，从数学活动角度出发，数学活动经验可分为数学化经验、逻辑联结经验和数学应用经验.从目前课堂教学的流程来看，多数课堂教学都由知识引入、知识关联、知识应用和知识总结等几个主要环节构成，而数学活动经验的习得更多来自课堂，数学素养的培育落脚点在课堂.下面笔者以苏科版《义务教育教科书·数学》九年级上册“2.5直线与圆的位置关系（3）”一课的教学为例，围绕数学课堂教学的几个主要环节，谈谈如何引导学生积累数学活动经验.

一、在知识引入环节注重学生数学化经验的获得

数学化经验就是学生在经历生活世界向数学世界的转化过程中，利用观察、实验、归纳、类比、猜测等方法对具体事物进行抽象概括的过程中所获得的经验.数学化经验主要指抽象化和概括化的经验.

环节1：情境创设.

师：要从如图1所示的一块三角形铁皮余料中剪一个圆，如何使剪得圆的面积最大？

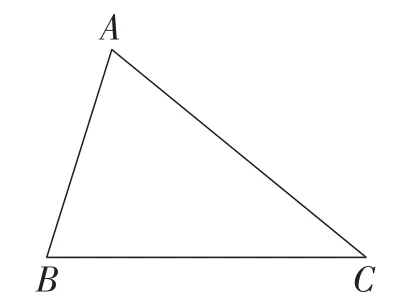
图1

师生活动：在学生充分思考后，教师通过几何画板软件演示寻找最大面积的圆，使学生的思维随着图2到图5的变化逐渐清晰起来.

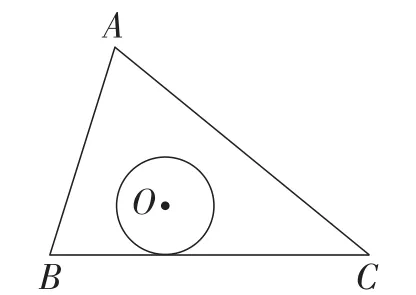
图3

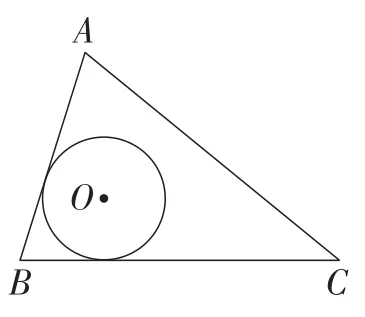
图4

图5

问题1:要剪出这个圆，关键要找到什么？

问题2：上面4个图中，哪个圆的面积最大？此时，⊙O与三角形三边的位置关系是什么？

问题3：由三条边都是切线你想到了什么？

问题4：一个三角形有几个内切圆？为什么？

环节2：概念介绍.

问题1：结合图6，能否给三角形的内切圆下个定义？

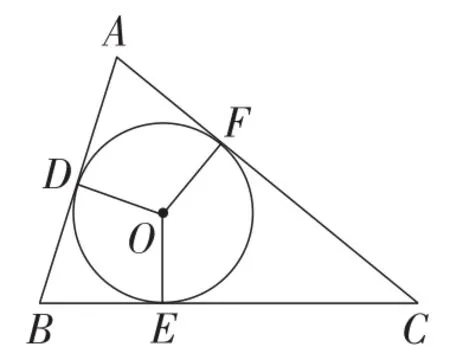
图6

问题2：三角形的内切圆和圆的外切三角形的“内”和“外”两个字如何理解？“切”字又如何理解？

在知识引入环节，从实际生活中的三角形铁皮余料中剪出一个圆的问题，可以抽象成在一个三角形中画一个圆，并且使圆的面积最大，将实际问题转化为数学问题.这一过程就是让学生从具体情境中经历初步抽象、获得抽象化的经验.学生经过探究，发现圆的面积最大时，就是其和三角形的三边都相切的时候，本质就是在三角形内部作一个圆，使它与三角形的三边都相切.这时需要知道圆心和半径，圆心要到三条边的距离相等，所以圆心在三角形三个角的平分线上，画出其中两个角的平分线，就可以确定出圆心.半径就是圆心到三条边的垂线段，过圆心作一边的垂线段就确定了半径.这一过程中，学生经历去情境化，联想到切线的性质，提炼出本质属性，使所研究的实际问题变成纯粹的数学问题，获得了数学化经验.在探究的过程中，学生理解了三角形的内心是怎样形成的，为什么它是三角形角平分线的交点，知道了知识产生的来龙去脉，更重要的是在探究的过程中获得了隐性的数学知识和抽象、概括的经验，发展了数学思维能力，积累了提炼概括化的经验，提升了数学素养.

二、在知识关联环节注重学生逻辑联结经验的提升

逻辑联结经验是学生在经历数学的逻辑联结过程中获得的经验，是学生在数学学习中，借助分析、对比、分类、演绎等思维方法，对已有知识再加工得到新的知识，以及对已有知识进行整理形成公理形式体系的过程中获得的经验.逻辑联结经验主要指知识扩充的经验和知识系统化的经验.

环节3：概念辨析.

如下表所示，对比三角形的外心和内心，你能说说它们的特征吗？

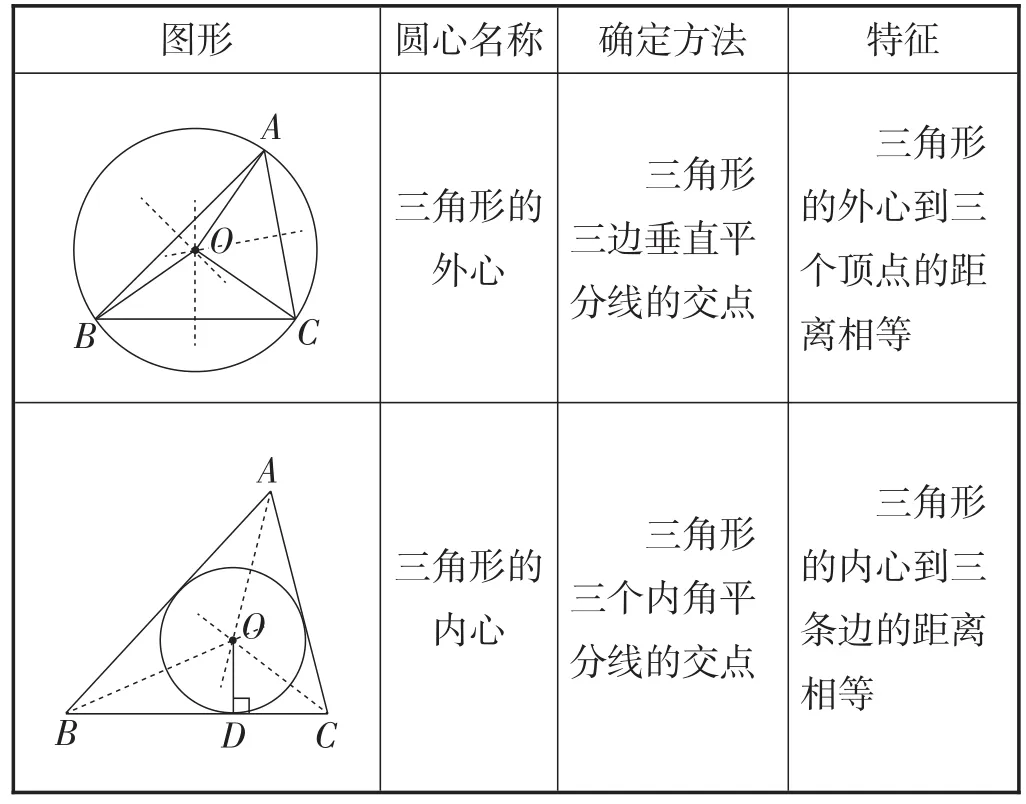
图形 圆心名称确定方法A OO 三角形的外心特征B C三角形三边垂直平分线的交点三角形的外心到三个顶点的距离相等A O三角形的内心三角形三个内角平分线的交点三角形的内心到三条边的距离相等B D C

环节4：概念延伸.

师生活动：教师出示相关图形，学生结合图形给出定义.与四边形各边都相切的圆叫做四边形的内切圆，这个四边形叫做圆的外切四边形.

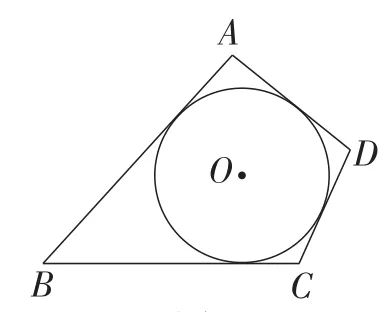
图7

如图7，四边形ABCD是⊙O的外切四边形，⊙O是四边形ABCD的内切圆.

以此类推，与多边形各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形.

在概念辨析环节类比三角形外接圆的学习经验，辨析三角形内心和外心的特征，在对比中体会它们的区别与联系，更好地掌握它们各自的特征.学生在建构新知识的过程中必然会和已有的知识建立联结，在联结的过程中进行对比、辨析，加深了对内心和外心两个概念的理解，不但经历了知识与方法的对比，而且提升了知识系统化的经验.在概念延伸环节，把在研究三角形内切圆的过程中积累的经验进一步发展，得到四边形的内切圆和多边形的内切圆的概念，让学生经历从特殊到一般的过程，感受数学知识扩充的经验，发展了学生的数学学习能力，提升了学生的学科素养.

三、在知识应用环节注重学生分析问题和解决问题经验的积累

分析问题和解决问题的经验是应用数学知识解决问题必备的经验.解决数学问题不单单是要解决某个数学问题，而是由点及类，获得解决同类其他数学问题的经验.分析问题和解决问题的经验主要指审题、分析问题的经验，以及提炼解题模式的经验.

图8

环节5：概念应用.

例1如图8，在△ABC中，点O是内心.

（1）若∠ABC=60°，∠ACB=70°，则∠BOC=______.

（2） 若∠A=80°，求∠BOC的度数.

（3）若∠A=n°，则∠BOC=______.（用含n的代数式表示.）

变式：在△ABC中，点O是外心，若∠A=n°，则∠BOC=______.（用含n的代数式表示.）

例2如图9，在△ABC中，内切圆I与边BC，CA，AB分别相切于点D，E，F，∠B=60°，∠C=70°，求∠EDF的度数.

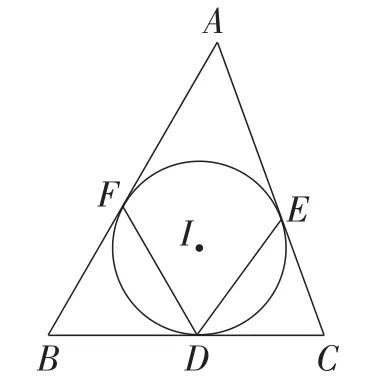
图9

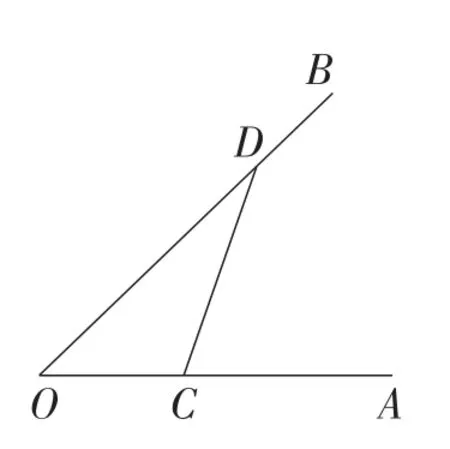
图10

例3如图10，OA，OB是两条射线，点C，D分别在射线OA，OB上.求作⊙P，使它与OA，OB，CD都相切.

例1的主要目的是强化学生对内心是如何产生的进行理解.学生经过分析，发现OB，OC此时都是角平分线，从而解决问题.在第（3）小题中让学生感受从特殊到一般的数学思想.变式训练让学生对容易混淆的内心和外心两个概念再次进行区分，获得解题的经验，同时提炼解决这类问题的通法.例2进一步强化了学生对内心的理解，也就是研究三角形内切圆的经验.根据题意分析内切圆与三边都相切，三条边都是圆的切线，想到连接内心和切点得到垂线段，从而使问题得以解决.例3强化了对知识引入中的数学活动经验的积累，让学生提取刚刚积累的活动经验并将活动经验进行迁移.这几道例题不但让学生积累了审题、分析问题的经验，也通过总结、思考，获得了提炼解题模式的经验，发展了数学素养.

四、在知识总结环节再生学生数学活动的经验

在知识总结过程中引导学生进行反思，通过反思，将学生的数学活动经验由原有的知识性层面上升到思想方法层面，形成意识和习惯，也就将原有的较低水平的活动经验再生为成熟稳定的活动经验.

环节6：总结提升.

问题1：通过本节课，你学到了什么？

问题2：你能说说三角形的外心和内心的特征吗？

问题3：你掌握了哪些研究问题的方法？

问题1不但让学生回顾了本节课所学的与内心的相关知识，也让学生总结了所经历的研究数学问题的过程，积累了数学活动经验.问题2对比内心和外心的特征，让学生掌握解决内心和外心问题的方法，提炼处理这类问题的经验.问题3使学生原有的经验进一步升华，经历“原始经验—再生经验—概括性经验”，从而形成成熟、稳定的数学活动经验.

数学活动经验是从数学活动中获得的，而数学活动更多的落实在平时的课堂上.教师在课堂教学的各个环节中要积极创设有效的活动情境，让学生不断积累数学化经验、逻辑联结经验和数学应用经验，从而丰富、发展学生的数学活动经验，让课堂成为学生积累数学活动经验的殿堂，只有这样，才能真正提升学生自身的数学核心素养.