小网格 大舞台
——以2018年天津市中考网格作图题的研究为例
宋 春,刘金英,赵国华
(天津市滨海新区塘沽第六中学;天津市中小学教育教学研究室;天津市滨海新区塘沽教育中心)
网格中的几何作图问题是近几年天津市中考探索的新题型,具有立意新颖、综合性强、思维含量高等特点,能有效的考查学生的数学核心素养.笔者以2018年天津市中考数学试卷第18题为例进行拓展研究,以期抛砖引玉.
一、试题呈现
题目如图1,在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均在格点上.
(1)∠ACB的度数为________;
(2)在如图所示的网格中,P是BC边上任意一点.以点A为中心,取旋转角等于∠BAC,把点P逆时针旋转,点P的对应点为P′.当CP′最短时,试用无刻度的直尺,画出点P′,并简要说明点P′的位置是如何找到的(不要求证明).
此题体现了《义务教育数学课程标准(2011年版)》(以下简称《标准》)对作图的要求,即在尺规作图中了解作图的道理,保留作图痕迹.同时,考查了学生利用网格,综合运用数学知识解决问题的能力,属于“综合与实践”的范畴.题目虽小,却蕴含着浓重的思维含量和进一步研究的价值,为后续教学中教师的教和学生的学,提供了极好的素材.
网格作图问题承载了学生的几何直观能力、发现与探究能力、逻辑推理与合情推理能力等,是中考命题的热点.例如,2018年北京、福建、海南、宁夏、四川广安、黑龙江齐齐哈尔,山东威海等地区的中考试卷中,均设置了相关问题.
为什么命题者对网格作图题如此青睐呢?笔者认为原因有以下五点:第一,有利于考查“图形与变换”的性质;第二,有利于考查图形与直观;第三,有利于考查学生“综合与实践”的能力;第四,有利于考查学生逆向思维能力;第五,有利于命题者打磨出精品试题.
二、试题研究
1.探源头,深挖教材找关联
人教版《义务教育教科书·数学》九年级上册习题23.1第1题第(1)小题“任意画一个△ABC,作下列旋转:以点A为旋转中心,把△ABC逆时针旋转40°”,此题是考查旋转的基本作图题,可以借助圆规和量角器完成,作用是巩固旋转的性质.习题23.1第4题“如图2,分别画出△ABC绕点O逆时针旋转90°和180°后的图形”,此题尝试在网格中作旋转,可以将△OAB逆时针旋转90°,找到点A,B的对应点A′,B′,再找到点C的对应点C′,就可以画出△ABC绕点O逆时针旋转90°后的图形(如图3).此题用无刻度的直尺就可以完成,其依据是在网格中可以借助全等三角形构造等腰直角三角形.

图2
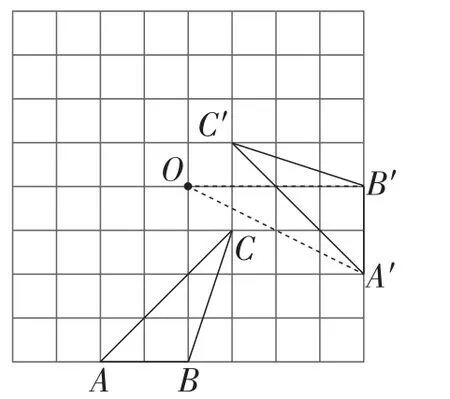
图3
从这两道简单的教材习题来看,旋转作图问题可以有效地帮助学生加深对相关问题的理解,这与2018年天津市中考试卷第18题的情境设计、问题本质、思考方法有很多相似的的地方.
2.探解法,变换角度寻路径
题目第(1)小题中,∠ACB=90°.第(2)小题的作法与分析如下.
作法1:如图4,取格点D,E,连接DE交AB于点T;取格点D′,E′,连接D′E′交CD于点K; 取格点M,N,连接MN交BC延长线于点G;取格点F,连接FG交TC延长线于点P′,则点P′即为所求.

图4
作法2:如图5,取格点D,E, 连接DE交AB于点T; 取格点D′,E′,连接D′E′, 取格点I, 连接TI交D′E′于点H;取格点M,N, 连接MN交BC的延长线于点G;取格点F,延长FG交AH的延长线于点C′;延长TC交C′F于点P′, 则点P′即为所求.
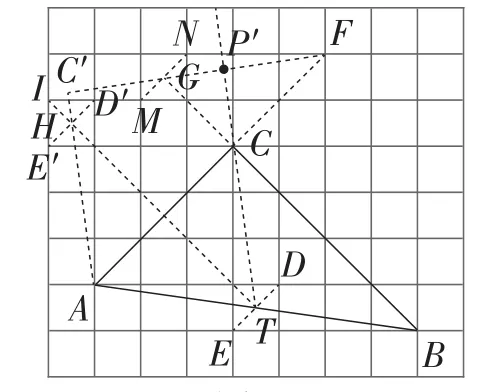
图5
解析:因为∠DAC=∠D′AC=45°, 再构造∠DAT=∠D′AH,即可构造出∠CAH=∠CAT.又由作法1可知∠F=∠B,AF=AB, 得到△C′AF≌△CAB.则∠AC′F=∠ACB=90°.由作法2可知AT=CT,则∠CAT=∠ACT.易得∠CAC′=∠ACT.从而有TC∥AC′. 所以CP′⊥C′F.
作法3:作法同作法2,利用解析式法求解,即在网格中建立平面直角坐标系,通过直线解析式确定特殊点的坐标,使问题方便求解.
解析:如图6,以A为原点,AD为x轴,AD′为y轴建立平面直角坐标系,
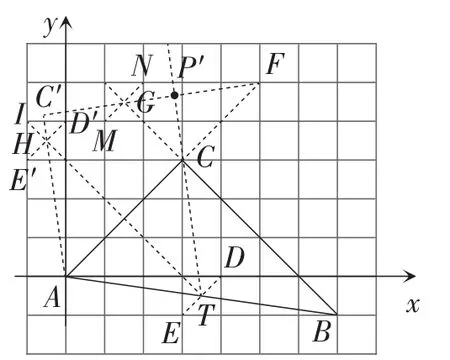
图6
可得直线AH的解析式为y=-7x.
由作法2可知FC′⊥AC′.

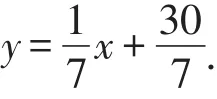
由CP′∥C′A, 则直线CP′的解析式为y=-7x+24.
作法4:如图7,取格点D,E, 连接DE交网格线于点K;取格点D′,E′,I,I′, 连接D′E′,II′交于点H; 取格点M,N,M′,N′, 连接MN,M′N′交于点G;取格点F,延长FG交AH的延长线于点C′;延长CK交FG于点P′,则点P′即为所求.

图7
解析:作法4中构造全等三角形的方法同方法2,即构造△C′AF≌△CAB.若要解决CP′⊥C′F的问题,由三角形全等可知∠AC′F=∠ACB=90°,为此利用同位角相等构造CP′∥AC′.
由作法4可知∠KDC=∠KCD=∠HAD′,得∠HAF=∠KCF.所以AH∥CK.所以CP′⊥C′F.
作法5:如图8,取格点D,E, 连接DE交网格线于点K;取格点D′,E′,I,I′, 连接D′E′,II′交于点H;取格点M,N,M′,N′, 连接MN,M′N′交于点G;取格点F,延长FG交AH的延长线于点C′;延长AC′交网格线于点F′;连接CK交FG于点P′,则点P′即为所求.
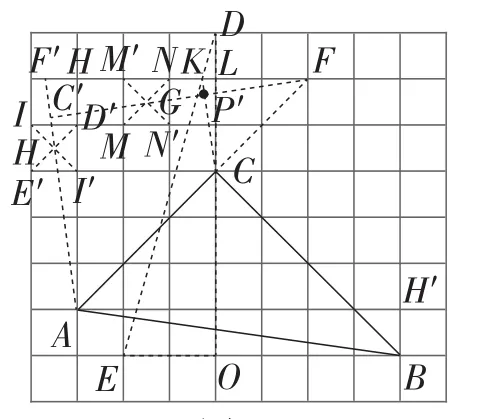
图8
解析:作法5中构造全等三角形的方法同方法2,即构造△C′AF≌△CAB.若要解决CP′⊥C′F的问题,由三角形全等可知∠AC′F=∠ACB=90°,为此借助成比例线段构造CP′∥AC′.

从上述作法不难发现,五种作法的共同点是构造全等三角形或相似三角形,关键是找到判定三角形全等的条件.作法2的思考路径较简捷,说明此题借助几何直观解决更方便些.作法4和作法5在构造两直线平行时,需考虑等角或对应线段成比例,方法巧妙,但不容易发现.这就是网格中存在的隐含条件,需要在网格中发现基本图形,如相似、全等、平行、垂直等.对于作法1和作法2,若能以数思形,借助图形进行直观分析,就可以迅速获得隐含条件,使问题形象、简明地得以解决.
三、进一步思考
1.网格作图题可以提供解决几何问题的多种途径
在网格背景下研究平面图形,一方面,能保留图形自身的几何特性;另一方面,网格自身的位置及数量的特殊性,使得图形中存在一些特殊关系,进而使图形的一般几何性质得以特殊化和数量化.网格作图给学生提供了多角度探究问题的方法,由于构图时可以选用网格中的特殊点,为学生拓展和创新搭建了平台,进而可以通过图形的旋转、平移、翻折、位似变换来构图,可以先画后证,还可以根据图形的特点及运算的需要,在网格中建立平面直角坐标系,用解析法确定点的位置、直线的位置关系等.
2.网格作图题可以考查学生的综合能力
此题的解决过程,从知识层面上,主要考查了勾股定理、成比例线段、相似三角形、全等三角形、直角三角形斜边上中线的性质、旋转作图等;从技能层面上,主要考查了学生的计算能力、作图能力和推理能力,其核心是构造全等三角形,作出平行和垂直;从基本思想方法来看,主要考查了数形结合、几何直观、化归思想、函数思想等.
3.网格作图题可以搭建培养学生创新思维的广阔舞台
此题属于“综合与实践”范畴,《标准》要求达到结合实际情境、经历设计解决具体问题的方案,并加以实施的过程,体验建立模型、解决问题的过程,并在此过程中,尝试发现和提出问题.通过对有关问题的探讨,进一步理解有关知识,发展应用意识和能力.网格中的基本作图包括:构造相似三角形、全等三角形、平行、垂直、n等分线段,作轴对称、平移,等等,这为学生创造性地应用数学知识解决问题提供了条件.在网格作图题中,只有熟练掌握基本图形的基本性质,将图形的变换了然于胸,才能在运用的过程中实现知识与技能的升华.
网格作图给学生提供了多角度探究的空间,构图时可以选取网格中的特殊点,增加解题的灵活性和创造性.网格作图是以学生的经验为基础,在短时间内完成构图、分析、验证和精准的判断,根据学生的自身能力及特点,可以展现出不同水平、不同角度的问题解决的方式,这彰显了网格潜在的庞大功能,即依托小网格,铸就大舞台.

