在观察与联想中进行整体建构
——2017年天津市中考试卷第25题评析有感
刘家良
(天津市静海区沿庄镇中学)
观察是发现、分析和解决问题的思维端口,而联想是架起知识之间、问题之间纽带的一座桥梁,观察、联想两者之间相辅相成.整体建构是解答中考压轴题的策略之一,在整体建构中朝着目标方向去变形,灵活善变、异中求同,并从中提炼出思想方法,这就需要观察与联想的助力.细品2017年天津市中考试卷第25题,笔者深有感触.
一、试题解析
题目已知抛物线y=x2+bx-3(b是常数)经过点
(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t) 为抛物线上的一个动点,点P关于原点的对称点为P′.
①当点P′落在该抛物线上时,求m的值;
②当点P′落在第二象限内,P′A2取得最小值时,求m的值.
分析:此题是2017年中考天津卷的最后一道试题,其中第(2)小题②问是此题的压轴一问.第(1)小题用待定系数法求抛物线的解析式,由抛物线的顶点坐标公式求顶点坐标.此小题面向全体,考查二次函数的基础知识和基本技能;第(2)小题第①问需要综合多个知识点:关于原点对称的点的坐标规律,图象上的点的坐标与函数式的关系,解方程(组).其中消去未知数t变二元为一元,是解m值的关键所在,需要学生具有观察、迁移和灵活的思维,此问检测了中等生对相关知识的综合运用能力;第②问具有较强的甄选功能:根据坐标的几何意义构造直角三角形,确立P′A2的函数式,是破解此题的第一道突破口,将P′A2函数式中含有的两个自变量m与t,设法变成含有一个自变量(m或t)的解析式是拦在众多学生面前的一道“坎”,要越过这道“坎”,就要依据m和t的关系,将m用含t的式子表示,或将t用含m的式子表示,这其间蕴藏的悉心观察、注重联系、善于变形、整体建构,是解m值的一条思维主线.
解:(1)将点A(-1,0) 代入y=x2+bx-3中,
得1-b-3=0.
解得b=-2.
所以y=x2-2x-3.
得顶点坐标为(1,-4).
(2)①因为点P′与点P(m,t关于原点对称,
所以点P′的坐标为P′(-m,-t).
因为点P,P′都在抛物线y=x2-2x-3上,
所以m2-2m-3=t,m2+2m-3=-t.
两式相加,得2m2-6=0.
② (方法1)由题意,知点P(m,t) 在第四象限内,
所以m>0,t<0.
由x2-2x-3=0,得
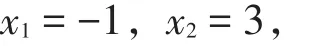
即抛物线y=x2-2x-3与x轴的交点坐标为(-1,0),(3,0).
因为点P(m,t) 为抛物线上的点,
所以0<m<3,m2-2m-3=t.
所以m2-2m=t+3.
由两点间的距离公式,得
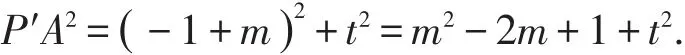
所以P′A2=t2+t+4.
因为0<m<3,
(方法2)由题意,知点P(m,t) 在第四象限内,
所以m>0,t<0.
由x2-2x-3=0,得
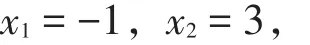
即抛物线y=x2-2x-3与x轴的交点坐标为(-1,0),(3,0).
因为点P(m,t) 为抛物线上的点,
所以0<m<3,m2-2m-3=t.
P′A2=
因为0<m<3,
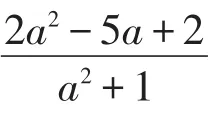
二、教学启示
《义务教育数学课程标准(2011年版)》指出,学生学习应当是一个生动活泼的、主动的和富有个性的过程.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.将观察放在学习活动过程之首,可见观察在学习活动中的重要地位.
解题是对所求对象(数、式、图形等)的观察、联想、比较、思考和发现的系列过程,在寻找“蛛丝马迹”的线索中开启思维之门.主动观察、善于思考,表现在将条件(已知)和结论(未知)化为一体的综合性联动,将整体和局部联系在一起做出宏观分析和微观思考.例如,整体替换法、构造法、换元法等,使求解过程呈现出巧妙、灵活、简约的思维气息,从而达到锻炼学生思维灵活性和深刻性的目的.因此,教师要为学生创设一些通过观察而使解题过程变得简捷的题目,引导学生体验观察为解题带来的便捷,并由此认识到观察在数学学习活动中所占的重要地位.
案例1:已知a2-2b=2,求式子2a2-4b-3的值.
此题学生如果直接计算也可以得到所求结果,但是若仔细观察所求式子和已知之间的数量关系,就会化复杂为简单.
师:有思路的同学请举手.

师:赋值法能化抽象为具体,这种方法值得大家去学习.
生2:由a2-2b=2,得a2=2+2b,代入所求式子,得2(2+2b)-4b-3=1.
师:将所求式子变为只含有一个字母的式子,需要将已知式子中的一个字母用含另一个字母的式子表示.运算过程中恰好消去了b,得到所求结果.
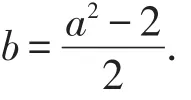
师:生3类比生2的方法,得到了所求结果.善于借鉴别人的经验,值得大家学习.
生4:观察所求和已知,发现所求和已知之间有一种内在的联系,所求式子中的2a2-4b=2(a2-2b)=4,这样顺利得到结果为1.
师:大家分享的4种解法中,生4的解法最为简捷.大家能说说为什么吗?
生5:生4没有忙于计算,而是善于观察已知和所求式子之间的联系,把已知和所求式子进行挂钩,巧妙得出结果.
师:解题前需要观察.观察是我们学习、思考问题的一扇窗.
案例2:如图1,两圆是以点O为圆心的同心圆,大圆的弦AB切小圆于点C,AB=8,求由两圆组成的圆环面积.
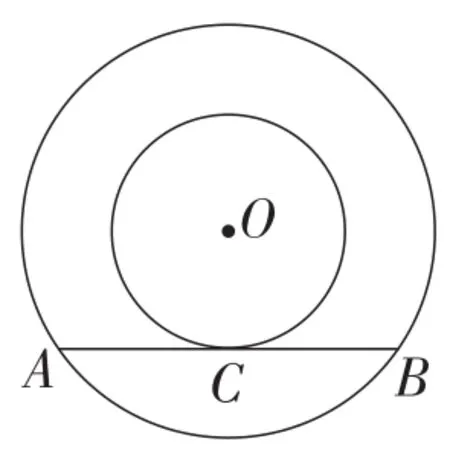
图1
师:大家表达自己的想法和解法.
生1:求圆环面积,需知两圆的半径,而两圆的半径都是未知的.至此我就解不下去了.
生2:“见切线,连半径”,如图2,连接OC,OA,则OC⊥AB.再也没什么线索了.
师:图中有了大圆和小圆半径了,可列式试一试.
生3:πOA2-πOC2,还是没有头绪啊!
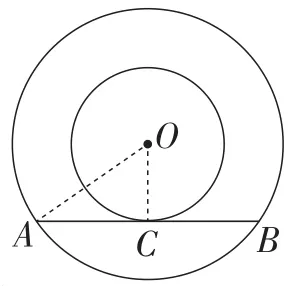
图2
生4:πOA2-πOC2=π(OA2-OC2).而这里的OA2-OC2=AC2,至此“案子”已破.
师:生4将大圆半径、小圆半径,还有弦长的一半通过勾股定理这个媒介融合在一起,巧妙地得出圆环的面积.彰显了观察与联想的魅力,体现了整体思想的魅力.
观察与联想是解题者展翅飞翔的羽翼,需要教师提供素材并慢慢的引导,逐步使学生认识到两者的魅力所在,逐步养成主动观察、善于联想的思考习惯,逐步使思维视线由局部向整体转移.

