注重思路转化 启发数学思维——一道几何问题的解题思考

齐 欣

（山东省临清市京华中学）

有效的解题教学通过合理的审题培养学生识图、用图的能力，将题目的特点转化为有效的解题方法.以学生发展为本，坚持低起点切入，积淀基本数学思想和基本方法，引导学生发现通法，注重关联，善于指导学生对解题思路进行深入分析及解后反思，这样解题之法就会自然、清晰地呈现在学生脑海中.笔者现将自己对一道几何填空题的解法探究整理成文，期待同行指正.

一、原题呈现

题目如图1，正方形ABCD的边长为6，点O是对角线AC，BD的交点，点E在CD上，且DE=2CE，连接BE.过点C作CF⊥BE，垂足为点F，连接OF，则OF的长为_____ .

图1

二、探寻解法过程

思路1：借助旋转变换，构造全等

由CD=6，又DE=2CE，可知DE=4，CE=2.在Rt△BCE中，由BC=6，CE=2，知于是由弦高公式，得从而BF=注意到OB=OC=32，且可证∠OBF=∠OCF，已具备一边、一角分别相等，因此可在线段BF上截取BG=CF，构造全等三角形为突破口.

解法1：如图2，在线段BF上截取BG=CF，连接OG.

图2

因为∠OBG=45°-∠CBE=45°-∠ECF=∠OCF，

又OB=OC，

所以△OBG≌△OCF.

从而OF=OG，∠BOG=∠COF.

所以∠FOG=∠COF+∠COG=∠BOG+∠COG=∠BOC=90°.

当然，此题也可以作OG⊥OF来构造全等解决，本质是一样的，都是借助如图3所示的旋转变换模型引路.

图3

思路2：借助四点共圆，导角定相似

由∠BOC=∠BFC=90°，可知点O，F均在以BC为直径的半圆上.据此，在四点共圆的条件下，可进一步挖掘、探究角的关系，往往相似易于获得.

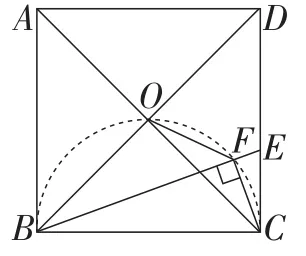
图4

解法2：如图4，由∠BOC=∠BFC=90°，

得B，C，F，O四点共圆.

所以∠BOF+∠BCF=180°.

所以∠BOF=180°-∠BCF=180°-∠BEC=∠BED，且∠OBF=∠EBD.

所以△BOF∽△BED.

解法3：同解法2，得B，C，F，O四点共圆.

所以∠OFB=∠ACB=45°=∠BDC.

因为∠DBE是公共角，

所以△BOF∽△BED.

【评析】事实上，在图1中，相似三角形（全等三角形除外）达20对.而恰恰就是包含OF，DE的这一对相似三角形的发现才是解决问题的关键.因此，抓住“边定全等，角定相似”，问题迎刃而解.

思路3：融推理于计算

除了导角，还有没有其他方法能得到△BOF与△BED相似呢？回到图1正方形背景中来看△BOF与△BED中以点B为端点的四条线段，显然夹公共角的四条边BO，BF，BE，BD的长都容易求出，因此，又可通过计算、验证得到的四条线段对应成比例，借助判别三角形相似的又一基本方法SAS来解决.融推理于计算是解题的突破口.

注：准确、快速求出BF的长是关键.

思路4：旋转变换，相似相伴

回看上述归纳的基本图形（图3），里面的两个等腰直角三角形显然是相似的.这是解题的一个突破口.

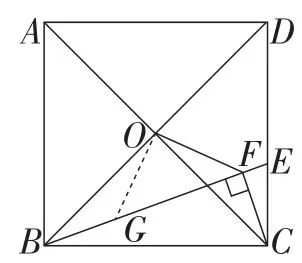
图5

解法5：由B，O，F，C四点共圆，得∠OFB=∠OCB=45°.

如图5，在线段BF上取点G，使OG=OF.

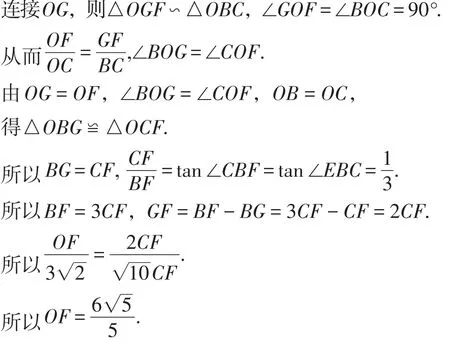
绕过“拦路虎”，再杀“回马枪”，及“关联问题思路受阻，要学会向上看，看我们已经得到了什么？”等等，这些都是教师在中考前经常交代学生的解题策略，用在这里进行解后反思，又有了新的发现.还有，CF，BF的长都是不必求出来的，原因是图1里面用图中字母表示的直角三角形三边之比都是确定的.

变式1：把图1放在坐标系中，以点B为原点，BC，BA所在直线分别为x轴、y轴，其余条件不变，求点F的坐标.

追问：OF的长和点O，F坐标之间有怎样的关联？

追问的意义在于由OF的长求不出点F的坐标，但是由点O，F的坐标却可以求出OF的长.

思路5：转化为解直角三角形

继续思考，再次结合条件观察△OFC，又有何新的发现呢？显然OC，CF已知，∠OFC=135°，原来这就是一个解直角三角形的基本图形（如图6），以此为突破口，得到解法6.

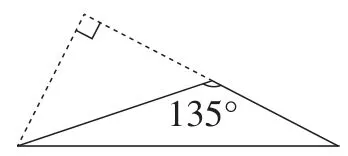
图6

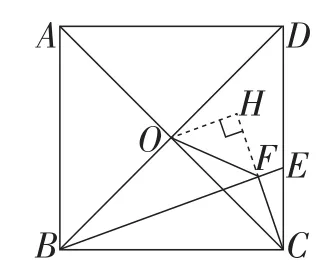
图7

解法6：如图7，作OH⊥CF，交CF延长线于点H，显然点O，F在以BC为直径的圆上，

还可以过点C作OF边上的高，或过点O作BC边上的高，思路是一样的.都是通过作垂线，构造直角三角形，并结合辅助圆及方程思想解决问题.对基本图形的运用是解法1至解法6，以及变式1解法的共性.

思路6：活用辅助圆

类比解法3、解法4，能否构造一个以OF为边的三角形与图中的关联三角形相似？继续思考，如果延长CF交BD于点M，容易发现△MFO与△MBC相似，以此为解题突破口.

解法7：如图8，延长CF交BD于点M，作MN⊥BC，垂足为点N.

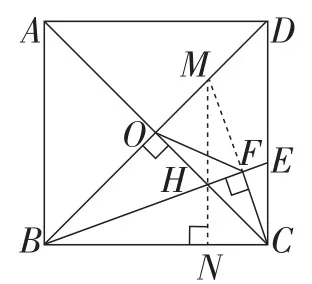
图8

借助辅助圆和相似三角形求解，作垂线构造直角三角形是关键.继续观察图8，容易发现△MHC与△OFC相似.

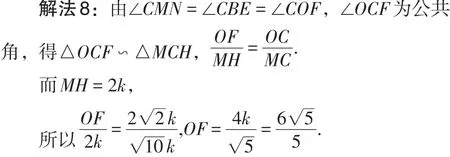
构造△MHC与△OFC相似是解题突破口.

思路7：巧借平行线

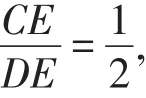
解法9：如图9，作CM∥BD，交BE的延长线于点M，

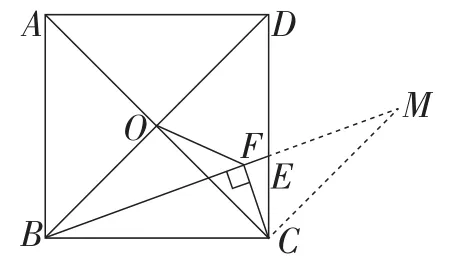
图9

借助相似的基本图形，求得ME的长是关键.正是“倍分关系寻相似，添线平行成习惯”.

思路8：构造中位线

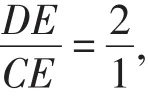
解法10：如图10，取ED的中点N，连接ON.

因为OD=OB，

所以ON为△BDE的中位线，ON∥BE.

延长CF交ON于点H，

则∠OHF=∠BFC=90°.

由EN=CE，ON∥BE，得

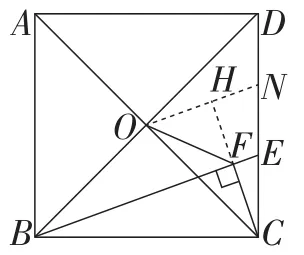
图10

由B，O，F，C四点共圆，得∠OFH=∠OBC=45°.

三角形中位线性质和判定，以及四点共圆的活用是解题的关键.

思路9：切换视角巧转化

解法11：如图11，作EH∥OC，交BD于点H，

变式2：正方形ABCD的边长为6，点O是对角线AC，BD的交点，点E在CD上，且DE=2CE，连接BE，交AC于点G，求BG，CG的长.

追问：继续求FG呢？

推广：正方形ABCD的边长为a，点O是对角线AC，BD的交点，点E在CD上，且DE=2CE，连接BE.过点C作CF⊥BE，垂足为点F，连接OF，则OF的长为_______（用含a的代数式表示）；如果DE=nCE，其他条件不变，则OF的长为___________（用含a的代数式表示）.

【评析】从解题策略上来说，方法要优化，正确是目的，效率是关键.

巩固练习：如图12，在△ABC中，∠ACB=90°，在BC上截取CD=AC，点E在AB上，∠CED=90°，CE=2，DE=1，F是AB的中点， 点G在CB上，∠GFB=2∠ECB.

（1）求FG的长；

（2）求证BE=BG.

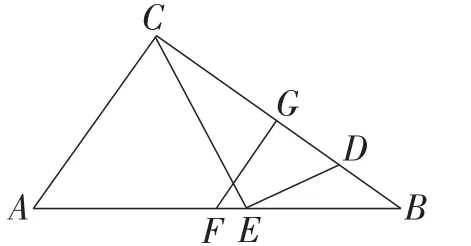
图12

【评析】发现FG∥AC是第（1）小题求解的关键，发现△BED∽△BCE是求解第（2）小题的关键.罗增儒教授曾说过，结论也是条件（从结论出发，BE∶BC=1∶2,等于DE，CE之比），从而得到思路.

三、解后反思

1.掌握审题要领是解法自然生成之钥

本文所述题目突出的是综合性、深刻性、灵活性、创新性.既体现在命题设计的原则上，又体现于笔者对审题和解题的感悟之中.合理的审题，迅速挖掘出题中包含的基本图形及特征，这往往会对解决相应的几何问题起到事半功倍的效果.审题的深入程度是决定解题顺利与否的关键.审题要辩证的看待问题的本质，及时发现合理地解题入口，从而迅速把握解题抓手.以上辅助线的添加、思路的探寻离不开合理、有效的审题.在已有认知经验基础上，通过众多信息的提取、组合，与已有模型关联、步步进阶，直至问题最终解决.

2.渗透数学思想是解法自然生成之本

充分探究试题多解，渗透对基本思想、方法的挖掘和相应的训练不仅有利于学生从大量烦琐的运算中解脱出来，而且有利于培养学生的求简意识和创新能力.回顾问题的解决，首先，从整体上把握，分出层次，排除干扰；其次，联想掌握的数学模型方法，渗透数学思想，从最容易发现的几个基本图形入手，用讲“故事（模型）”的方式，“采蘑菇（关联）”的方法将解法如何探究、生成、反思，以及完善的过程一一展示；最后，通过变式及推广，分别对解法做梳理，异中求同、举一反三.孔凡哲教授说过，数学模型是故事，解题永流传.借“图形”关联，明思维之道；用“故事”引路，优解题之术.体会数学问题都是运用所学过的知识加以解决的，知识转化才是一切转化思想与方法的本源.

3.启发数学思维是解法自然生成之源

数学的严谨呈现为“冰冷的美丽”，但是数学的发现却是“火热的思考”.以上解法不是凭空产生的，是基于尊重学生，尊重知识发展逻辑，坚持低起点切入，学生的思维自然而然地卷入其中，探求的愿望油然而生，逐步引导学生“由此向，及远方”，领略沿途“风景”，不知不觉中，实现解法自然生成这一目标.引导学生通过合理审题，激活其已有知识，注重基本图形性质，考查几何基础知识的应用和经验图形的积累，是几何教学中提高学生分析和解决问题能力的重要一环；注重基础、关注技能、突出经验、强化思想也是近几年各地区中考关于“图形与性质”内容考查的鲜明特色.通过方法的渗透和体验，让学生学会用数学的思想方法解决问题，掌握数学模型方法，逐步将思维引向深入，使学生在思维能力、思维习惯和数学意识上得到协调发展.

4.探寻知识关联是解法自然生成之魂

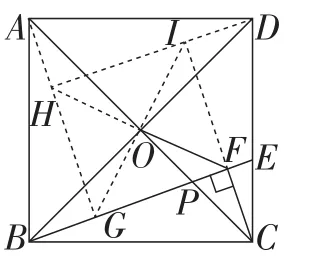
图13

因此，从创新的思维视角，探寻知识关联，让学生在探索过程中领略到问题的演绎及变式策略，深化认知结构和完善思维，学会变换思考问题的角度，是我们不懈的追求.