关注几何模型 破解线段最值
——以2017年中考数学试题为例
张 宁
(宁夏回族自治区中卫市沙坡头区宣和镇张洪学校)
近年来,在全国各地中考数学试题中经常出现有关线段或线段之和的最值问题,这类问题通常以线段、直线、三角形、四边形、圆等几何图形或函数图象为背景,考查学生综合运用所学知识分析问题和解决问题的能力.这类问题形式灵活多样,涉及的知识点较多,对学生而言具有一定的难度.解决这类问题的关键是要根据图形的基本特征,将线段或线段之和的最值问题转化为相应的几何模型,然后利用几何图形或函数图象的性质求解.笔者以2017年全国各地部分中考试题为例,说明几何模型在求线段或线段之和最值问题中的应用,供读者参考.
模型1:如图1,点A,B在直线l的同侧,作点A关于直线l的对称点A′,连接A′B,交直线l于点P,则此时PA+PB的长最短.
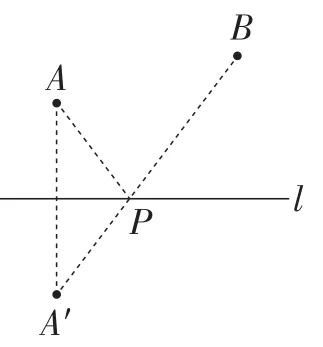
图1
这一模型通常称之为“将军饮马”问题,其本质是根据“两点之间线段最短”求最短距离的一个几何模型.
例1(湖北·孝感卷)如图2,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4) ,且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为________.
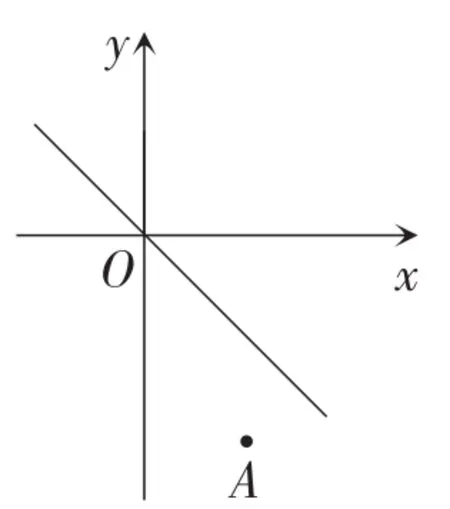
图2

图3
解析:由平移的性质易知点B的坐标为B(0,-2) .
如图3,作点B关于x轴的对称点B′,连接AB′,交x轴于点P.
由模型1知,此时PA+PB的值最小.
利用待定系数法,易求得直线AB′的表达式为y=-3x+2.
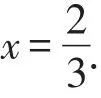

【点评】此题主要考查一次函数的性质、待定系数法、线段之和的最值问题等知识点.根据已知条件,点P为x轴上的动点,点A和点B为两个定点,符合模型1的基本特征.根据模型1,这里作出了点B关于x轴的对称点B′,然后利用待定系数法确定直线AB′的表达式,最终利用一次函数的性质求得点P的坐标.当然也可以作出点A关于x轴的对称点A′来解决问题,此处从略.
模型2:在等底等高的所有三角形中,等腰三角形的周长最短.
如图4,AD∥BC,△ABC和△DBC是等底等高的两个三角形,AB=AC,则AB+BC+AC<DB+BC+DC.①

图4
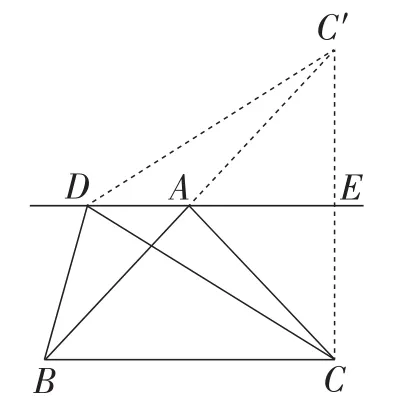
图5
证明:如图5,作点C关于直线AD的对称点C′,连接AC′,DC′,CC′,CC′交AD于点E.
易知AC′=AC,DC′=DC,∠C′AC=2∠EAC.
因为AD∥BC,所以∠EAC=∠ACB.
因为AB=AC,所以∠ABC=∠ACB.
因为∠ABC+∠ACB+∠BAC=180°,
所以∠BAC+∠C′AC=180°.
所以B,A,C′三点共线.
在△C′DB中,BC′<BD+DC′,即
AB+AC<DB+DC.②
从而可知,AB+BC+AC<DB+BC+DC.
【说明】为了叙述方便,模型2中比较的是两个三角形周长之间的关系,即不等式①.因为这类问题涉及到的图形是同底等高的一系列三角形,所以利用这一模型求解线段之和的最小值问题时,直接利用不等式②即可.显然,模型2是模型1的一种特殊情形,利用这一模型可直接求解相关问题,简化解题过程,提高解题效率.
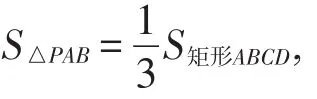

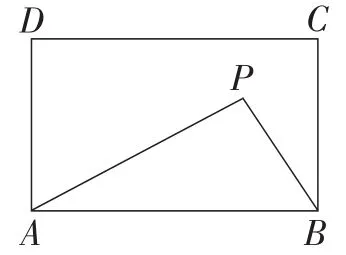
图6
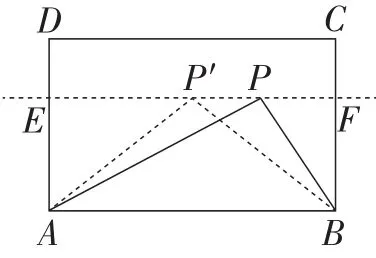
图7
解析:如图7,过点P作直线EF∥AB,分别交AD,BC于点E,F,易知动点P在直线EF上运动.

由模型2知,当△PAB是等腰三角形时,PA+PB的值最小.
当点P位于线段EF的中点P′处时,△P′AB是等腰三角形,此时PA+PB的值最小.
故此题选择选项D.
【点评】此题主要考查三角形与矩形的面积公式、勾股定理、线段之和的最值问题等知识点.根据已知易知,△PAB和△P′AB是等底等高的三角形,符合模型2的基本特征.由此可知,当点P位于线段EF的中点P′处时,△P′AB是等腰三角形,PA+PB的值最小.
模型3:直径是圆中最长的弦.
已知:在⊙O中,AB是直径,CD是弦.求证:AB>CD.
证明:假设AB<CD,连接OC,OD,则OC+OD=AB.
因为AB<CD,所以OC+OD<CD.

图8
这与公理“两点之间,线段最短”相矛盾,所以假设不成立.
所以直径是圆中最长的弦.
例3(海南卷)如图8,AB是⊙O的弦,AB=5,C是⊙O上的一个动点,且∠ACB=45°.若M,N分别是AB,AC的中点,则MN长的最大值是______ .
解析:因为M,N分别是AB,AC的中点,

图9
为使MN的长取得最大值,只需要BC的长取得最大值即可.
因为BC是⊙O的弦,所以当BC是⊙O的直径时,BC的长取得最大值.
如图9,过点B作⊙O的直径BC′,连接AC′,取AC′的中点N′,连接MN′.
易知∠AC′B=∠ACB=45°,∠BAC′=90°.

【点评】此题主要考查三角形中位线的性质、圆的性质、直角三角形的边角关系等知识点.利用“直径是圆中最长的弦”这一结论容易求得MN长的最大值,即过点B作⊙O的直径BC′,然后构造直角三角形是解决此题的关键.
模型4:给定两点A,B及第三个点P,则PA+PB≥AB,当且仅当点P在线段AB上(含点A,B)时,PA+PB取得最小值AB;当点P在AB的延长线上时,PA取得最大值AB+PB;当点P在BA的延长线上时,PB取得最大值AB+PA,不妨称之为三点共线原理.

(A)3 (B)4 (C)5 (D)6

图10

图11
解析:如图11,过点P作PC⊥Ox,垂足为点C.
因为F(0,2),M( 3,3)是定点,
要使△PMF的周长最小,只需PM+PF取最小值,即PM+PC取最小值,由图形易知,当M,P,C三点共线时,PM+PC即可取得最小值.
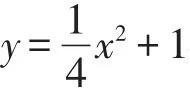
故△PMF周长的最小值为MF+MC′=2+3=5.
故此题选择选项C.
【点评】此题以抛物线为背景,主要考查平面直角坐标系内点到坐标轴的距离、两点之间距离的求法、勾股定理等知识点.根据已知,要求解△PMF周长的最小值,其本质是求PM+PF的最小值,根据三点共线原理容易解决.此题中已知“抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等”,在很大程度上降低了试题的难度.如果已知条件中没有给出这一结论,读者也可以自行计算说明.
模型5:已知⊙O外一点P和⊙O上任意一点Q,当点Q,O,P共线,且点P和点Q在点O的同侧时,PQ长度最小.
证明:如图12,连接OP,交⊙O于点Q′,连接OQ.

图12
由三角形的三边关系可知,PQ+OQ>OP,
即PQ+OQ>PQ′+OQ′.
又因为OQ=OQ′,所以PQ>PQ′.
所以当点Q在点Q′处时,PQ长度最小.
综上所述,当点Q,O,P共线,且点P和点Q在点O的同侧时,PQ长度最小.
例5(四川·内江卷)如图13,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE.
(1)求证:AC2=AE·AB;
(2)过点B作⊙O的切线交EC的延长线于点P,试判断PB与PE是否相等,并说明理由;
(3)设⊙O的半径为4,N为OC的中点,点Q在⊙O上,求线段PQ的最小值.
解析:(1)如图14,连接BC,证明△AEC∽△ACB即可,此处从略.
(2)如图14,连接OB,证明∠PEB=∠COB=∠PBN即可,此处从略.
(3)如图14,连接OP,交⊙O于点Q.由模型5知,此时PQ的长度最小.
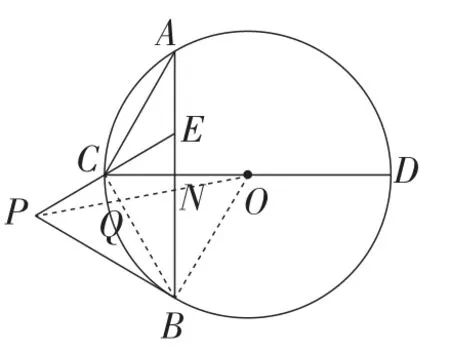
图14

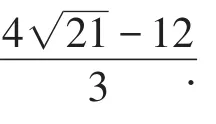
【点评】此题是圆的综合题,主要考查相似三角形的性质和判定、等腰三角形的性质、等边三角形的性质和判定、垂径定理、切线的性质、勾股定理等知识点.第(3)小题有一定的难度,确定PQ最小值时点Q的位置是解决问题的关键,根据模型5即可确定点Q的位置,然后利用勾股定理、方程等即可求出线段PQ的最小值.
总之,线段或线段之和的最值问题是初中数学学习的难点,几何模型是解决这类问题的基本工具.只有在学习中不断积累几何模型,才能有效地建立起基础知识与数学应用之间的桥梁.建立和处理几何模型的过程,就是将数学知识应用于实际问题的过程.建立模型更为重要的是,能够提高学生对几何事实的进一步认识,能够有效提高学生分析问题和解决问题的能力.

