理论交织结硕果 解题能力巧提升
——以一道旋转不变性问题为例
王 海,虞秀云
(江西师范大学数学与信息科学学院)
解题研究一直以来都是教育领域所关注的重点,波利亚的“怎样解题表”作为经典的解题理论之一,是开展解题研究的重要理论支撑.罗增儒教授的解题信息论则从不同方面提出了解题观点,但两者在解题思想和步骤上有许多神似的地方.
“怎样解题表”是《怎样解题》一书的精华,“怎样解题表”的四个步骤中,通过一系列提问,引导我们从不同的方面进行解题思考,给我们带来很好的解题思路.波利亚在《怎样解题》中提到“你能否想到一道更为普遍化的题目?能否想到一道更为特殊化的题目?”阐述了一般化与特殊化之间的联系.解题信息论认为,数学解题的过程就是数学问题信息的获取、存储、处理、输出,从而实现解题目标的运动过程.在数学解题过程中,大脑需要处理一系列的信息(题目的条件,有关的定理、定义和公式等),同时通过信息间的有效组合得出解题方法,从而解决数学问题.
在解题过程中,两种理论的交织使用,有利于数学解题能力的提高.“怎样解题表”主要从宏观层面上教会我们如何寻找解题思路,而解题信息论主要从微观层面上教会我们找到具体的解题方法.在实际解题中交织使用这两种理论,有利于解题思路与解题方法的产生.笔者以一道旋转不变性问题为例,谈谈如何利用这两种理论进行数学解题活动.
例1如图1,正方形ABCD和等腰直角三角形BEF中,连接DF,G为DF的中点,连接EG,CG,则EG和CG之间有什么数量关系和位置关系?并加以证明.
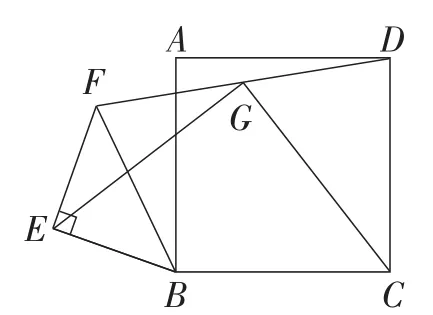
图1
一、理解题目,大胆猜想
“怎样解题表”的第一步提到,首先理解语言的陈述,并引入适当的数学符号.上述例题中的未知量是EG和CG之间有什么数量关系和位置关系;已知量是正方形ABCD、等腰直角三角形BEF、G为DF的中点.通过深入理解题目给出的条件,得到更多的结论,即AB=BC=CD=AD,∠A=∠ABC=∠BCD=∠ADC=90°,BE=EF,∠BEF=90°,∠EBF=∠EFB=45°, FG=DG.利用“怎样解题表”的第一步“你必须理解题目”,对题目的已知量和未知量进行分析,发现例1所给的条件并不充分,无法直接证明出EG和CG之间的数量关系和位置关系.根据“怎样解题表”的第一步和几何直观,猜想EG=CG,且EG⊥CG.
二、从一般到特殊,寻找解题思路
“怎样解题表”的第二步:找出已知量和未知量之间的联系;如果找不到直接的联系,你也许不得不去考虑辅助问题;你应该最终得到一个解决问题的方案.通过上面的分析,发现“不得不去考虑辅助问题”,即寻找一道更为特殊化的题目.我们知道,适用于普遍情况的,对其中的特殊情况也必能适用,这是逻辑方面的常识.从特殊到一般,是我们获得知识的最基本的途径.通过观察图1,发现正方形ABCD和等腰直角三角形BEF有一个公共点B,如果将等腰直角三角形BEF绕点B旋转,那么EG和CG的数量关系和位置关系是否会发生变化?这道题是否可以转化成一道旋转不变性的问题呢?本文选取了等腰直角三角形BEF在旋转的过程中的四种特殊位置的图形加以讨论,寻找解答例1的方法.
变式1:如图2,在正方形ABCD及等腰直角三角形BEF中,连接DF,G为DF的中点,连接EG,CG,则EG和CG之间有什么数量关系和位置关系?并加以证明.
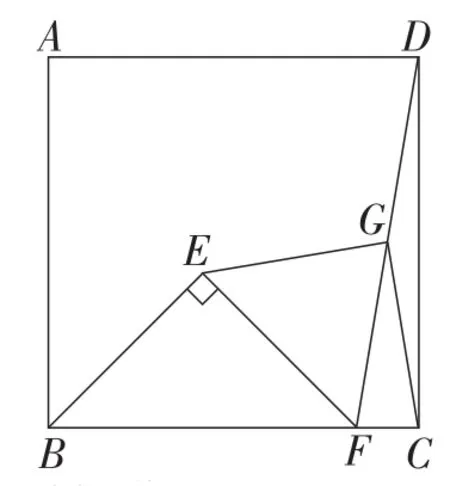
图2
思路探究:通过解题信息论的三步曲,寻找解题方法.连接ED,发现B,E,D三点在同一条直线上.
(1)有用捕捉,即从理解题意中捕捉有用的信息.根据题意,找出3条信息:△DCF是直角三角形;G是DF的中点;∠BDC=45°.
(2)有关提取,即从记忆存储中提取有关的知识信息.此题中的有关提取为:直角三角形斜边上的中线等于斜边的一半;一条弧所对的圆周角等于它所对的圆心角的一半;等式的性质.
(3)有效组合,将上述两组信息加工配置成为一个和谐的逻辑结构,详细过程如流程图3所示.
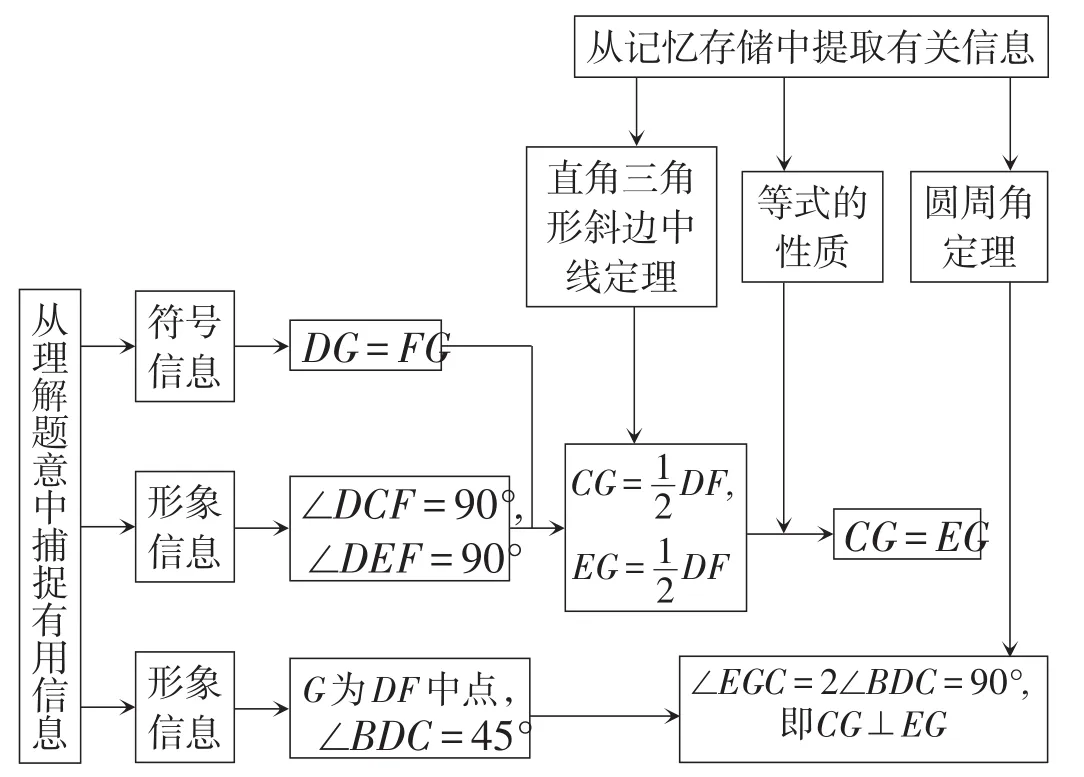
图3
变式2:如图4,在正方形ABCD及等腰直角三角形BEF中,G为DF的中点,连接EG,CG,则EG和CG之间有什么数量关系和位置关系?并加以证明.
思路探究:由于在解答变式1时,利用直角三角形斜边中线定理,间接得到了EG=CG.那么以DF为斜边构造直角三角形,作出辅助线,能否寻找到解题方向呢?
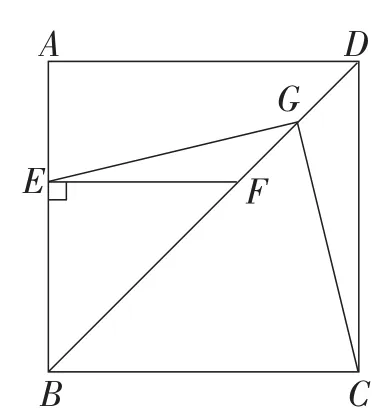
图4
(1)有用捕捉:△BEF是直角三角形;G是DF的中点;EF∥BC.
(2)有关提取:根据变式2,思考如何以DF为斜边构造直角三角形,发现EF∥BC.如图5,延长EF与CD交于点H,连接HG.由于EG和CG分别是△EGH和△CGD的两条边长,若能证明△EGH≌△CGD就能得到EG=CG.那么怎样证明△EGH≌△CGD是第一个难点.从图5可以看出∠EGC=∠EGF+∠FGC,只要证明∠EGF+∠FGC=90°,那么就能说明EG⊥CG成立.如何证明∠EGF+∠FGC=90°是第二个难点.

图5
(3)有效组合:利用△DFH是等腰直角三角形,GH为中线,得知GH=DG,∠GDC=∠GHE=45°.显然EH=DC.从而证明了△EGH≌△DGC(SAS),因此EG=CG,解决了第一个难点.由△EGH≌△DGC,可以得到∠EGH=∠DGC,即∠DGH+∠HGC=∠EGC+∠HGC,因为∠DGH=90°,所以∠EGC=90°,解决了第二个难点.
变式3:如图6,在正方形ABCD及等腰直角三角形BEF中,连接DF,G为DF的中点,连接EG,CG,则EG和CG之间有什么数量关系和位置关系?并加以证明.
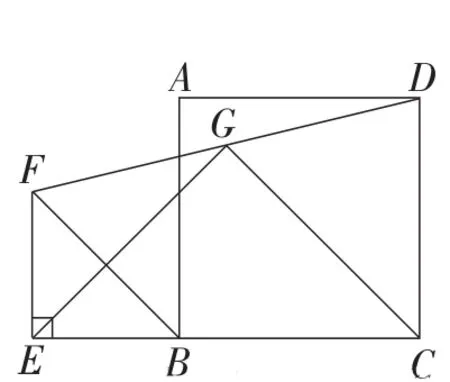
图6
思路探究:变式2中利用两个三角形全等,证明了EG=CG.而条件“G为DF中点,EF∥DC,DF与EF分别与DC交于点F和点D,那么是否可以通过作辅助线构造两个三角形全等来证明EG=CG呢?这使得我们想起一类辅助线作法的数学模型:如图7,在一个平面内,一条直线与一组平行线相交于A,B两点,过AB的中点G,任意画一条直线,与平行线相交于C,D两点,那么就能构造出两个全等三角形,即△ACG≌△BDG.
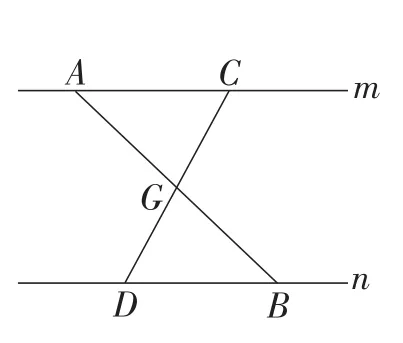
图7
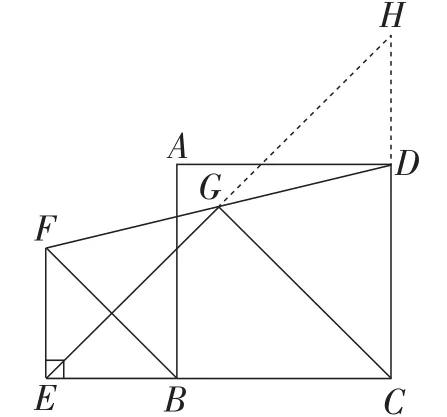
图8
根据该数学模型,在图6中延长CD与EG的延长线交于 点H(如图8). 因为 ∠FGE=∠DGH,FG=DG,∠EFG=∠HDG,所以△EGF≌△HGD(ASA).从而得到BE=EF=HD. 又因为BC=CD,∠ECH=90°,所 以△ECH是等腰直角三角形.根据EG=HG和等腰三角性三线合一的性质,可以得到EG=CG,EG⊥CG.
变式4:如图9,在正方形ABCD及等腰直角三角形BEF中,G为DF的中点,连接EG,CG,则EG和CG之间有什么数量关系和位置关系?并加以证明.
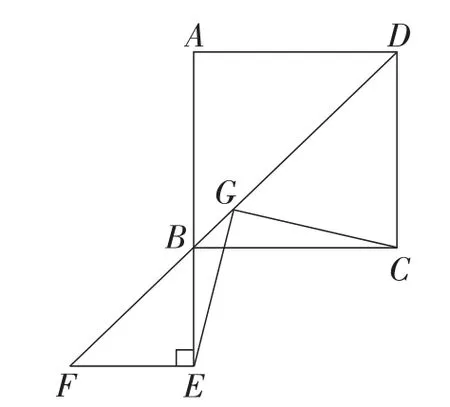
图9
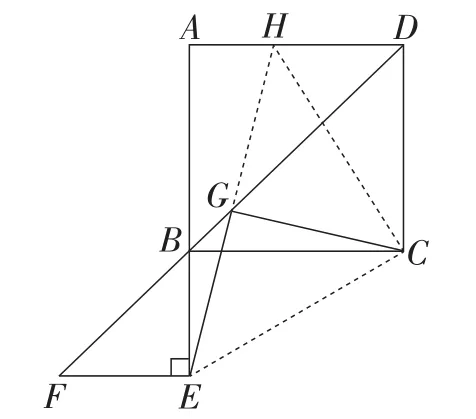
图10
解数学题时,应用数学模型去寻找解题思路,可以排除其他因素的干扰,提高思维的敏捷性.根据图7提到的一类辅助线作法的数学模型,如图10,延长EG,与AD交于点H,连接EC,HC, 因为△EFG≌△HDG,所以EF=HD,EG=HG.易证得△BCE≌△DCH.所以△ECH是等腰直角三角形,再根据EG=HG和等腰三角性三线合一的性质,可以得到EG=CG,EG⊥CG.
三、从特殊到一般,揭示本质
“怎样解题表”的第三步:执行你的方案,你能清楚地看出这个步骤是正确的吗?一方面,要审视推理得到的每一步的合理性;另一方面,对执行的方案的本质要洞悉清楚.例1实质上是建立了以点B为公共顶点的等腰直角三角形BEF和正方形ABCD,将等腰直角三角形BEF绕着点B旋转的模型,探讨等腰直角三角形BEF在旋转的过程中,EG和CG的数量关系和位置关系是否发生变化,然后选取了四种特殊位置的图形,证明了EG和CG的数量关系和位置关系不会发生变化.其实等腰直角三角形BEF旋转到任何位置,该结论依然成立.同时,建立了一种特殊的数学模型,解决了符合这一特征的一类问题.
例1是这类旋转图形的一般情形,也符合这一模型的使用条件.如图11,过点D作EF的平行线,交EG的延长线于点H,连接EC,HC,因为△EFG≌△HDG,得 到DH=EF,EG=HG.所以△BCE≌△DCH.所以△ECH是等腰直角三角形.从而得到EG=CG,EG⊥CG

图11
在例1的解题过程中,可以从几种特殊情况入手,寻找一般情形的解法,也能将一般情形的解法在其他特殊情形中应用,从而体现了特殊化思想与一般化思想两者的辩证统一.一方面,通过将一般性题目特殊化,去寻找一般化题目的求解方法;另一方面,通过将特殊性题目一般化,去解决这一类题目.
四、拓展应用,解决一类问题
“怎样解题表”的第四步提到:你还能在别的什么样的题目中利用到这个结果或方法吗?像例1类型的题目的解题思想和方法在其他许多题目上都能应用到,例如,在如下题目中就有所体现.
例2如图12,在△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,M是BC的中点,连接MD和ME,求证:MD=ME,MD⊥ME.

图12
由“怎样解题表”的第一步“理解题目”,得到如下条件:(1)理解语言的陈述,未知量为MD=ME,MD⊥ME;已知量为△ABD和△ACE是等腰直角三角形,M是BC的中点;(2)深入理解题目的条件,即AD=BD;AE=EC;∠D=∠E=90°;∠DBA=∠BAD=∠EAC=∠ECA=45°;BM=MC.但是以上条件并不是在每个解题中都会应用到,利用解题信息论的第一步“有用捕捉”,抓住关键条件BM=MC,BD=AD,AE=CE.
根据“怎样解题表”的第二步“拟定方案”,拟定解题方案如下:根据题目条件和图形,尝试利用前面的数学模型,构建两个全等的三角形,利用例1所展示的旋转不变性问题,通过证明等腰直角三角性,得到MD=ME,MD⊥ME.针对以上解题方案,结合解题信息论第二步“有关提取”,需要提取判定三角形全等的条件、平行线性质、三角形内角和定理、等腰三角形三线合一有关定理和性质,才能有效解决这道题目.
结合“怎样解题表”的第三步“执行方案”和解题信息论的第三步“信息间的有效组合”,得出解题方法如下:如图13,过点B作EC的平行线,与EM的延长线交于点F,连接DF,DE,因为△EMC≌△FMB,得EC=BF和EM=FM.所以△BFD≌△AED.所以△DFE是等腰直角三角形,所以MD=ME,MD⊥ME.
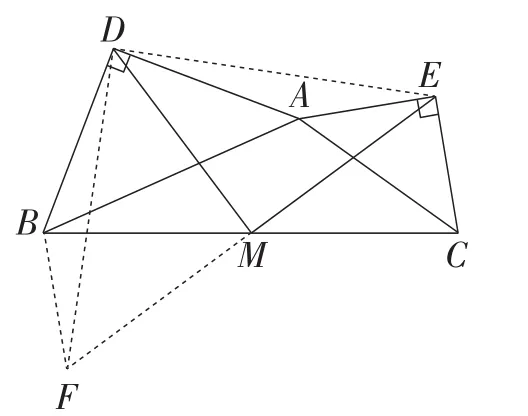
图13
最后,根据“怎样解题表”的第四步,检查已经得到的解答,强调回顾,包括解题方案是否合理,解题思路是否正确等.解题信息论强调解答依然向我们输入信息,表现为解后的探究.通过反思解题过程,提升自我监控能力;反思解题结果,完善认知结构;反思解题方法,优化思维品质;反思解题实质,促进思维的发展.波利亚的“怎样解题表”的第四步和解题信息论的解后探究正好诠释了这样一个道理:在解题教学中,教师更多的是要教会学生解题的方法和思想,而不是某道题的解法;每道题目的解决并不是学会解题的终点,而是学会解题的起点.
解题教学要以学生的思维为起点,追求自然合理的解法.在数学解题活动中,教师与学生的认识往往是不一样的,不能把教师的解题方法直接灌输给学生.文章利用波利亚解题四步骤和解题信息论三步曲从宏观上与微观上引导学生思考问题和寻找具体的解题方法,致力于拓展学生的思维空间,提升学生的思维能力,升华学生的思维境界,切实提高学生的解题能力.

