浅谈利用几何画板软件制作动点课件的方法
陈 翔,张瑞红
(湖北省宜昌市第三中学;黄冈师范学院计算机学院)
动点问题是大家关注比较多的一种题型,由于点运动到不同的位置时,图形也相应地发生改变,所以教师在讲解这类问题时如果借助几何画板软件画图会十分直观.下面笔者就这类问题的课件制作提供一些方法供读者参考.
例1在△ABC中,BC=4,高AD=3,点F沿边AC从A向点C运动,作EF∥BC交AB于点E,交AD于点G,以EF为斜边作等腰直角三角形PEF,且使点P,A在直线EF的异侧,设EF=x,△PEF与四边形BCFE重合部分的面积为y.
(1)当点P在线段BC上时,求线段AG的长;
(2)求y与x的函数关系式,并求x的取值范围.
在制作该题目的课件时,一般都想画出重叠部分的内部,并用醒目的颜色标识.此题显然有图1,图2所示的两种情况.情况1:如图1,当点P在△ABC内部时,重叠部分就是△PEF的内部.情况2:如图2,当点P在△ABC外部时,重叠部分是一个梯形的内部.
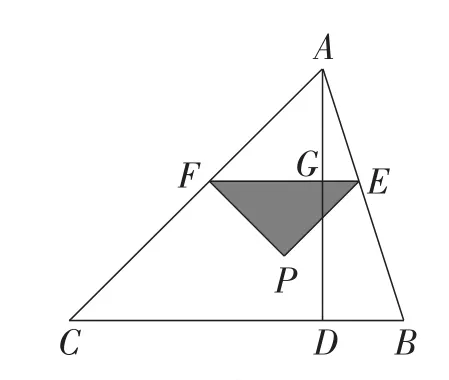
图1
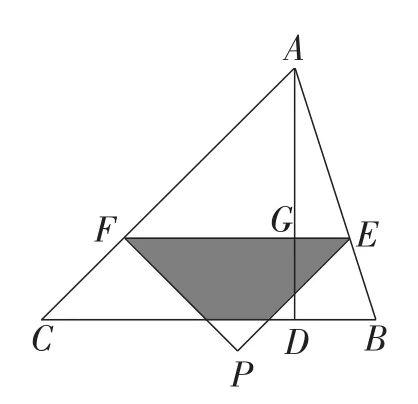
图2
如果利用几何画板软件先作出情况1时的△PEF的内部,那么它在情况2时仍然可见,这显然不行.下面介绍两种解决问题的方法供读者参考.
方法1:如果制作一个“隐藏/显示”按钮,使得在情况2时隐藏△PEF的内部,而在情况1时显示△PEF的内部,此时无法做到当点P刚刚到△ABC外部时就将△PEF内部隐藏,不够智能,所以这并不是最好的方法.笔者的思路是这样的:用∠PDA的度数作为控制△PEF内部的颜色参数.因为当∠PDA是锐角时,点P在△ABC的内部;当∠PDA是钝角时,点P在△ABC的外部.也就是说,当点P在△ABC外部时, 90°-∠PDA的值不存在,如果将△PEF内部的颜色参数设置为1+那么点P在△ABC的外部时,由于该值不存在,△PEF内部的颜色就不存在,因而不可见.具体作法是:先构造△PEF内部,并度量∠PDA的度数,再点击“数据”,计算的值,选中该值和△PEF内部,依次执行命令“显示、颜色、参数”,在弹出的对话框中,按图3所示的方式设置即可.

图3
实际上,1+0× 90°-∠PDA也可用1+0× 2.4-EF或代替,这里的2.4是当点P在边BC上时,EF的长度,1.8是当点P在边BC上时,AG的长度.
方法2:既然用常规方法所作的重叠部分的内部容易相互干扰,如果能做到两种情况下BC的平行线与AB的交点不同,就可以做到互不干扰.所以笔者将边AB以点E0为界分成上下两个部分(这里的E0就是当点P在边BC上时点E的位置),再隐藏线段AB,连接AE0,BE0,过点F作BC的平行线,分别作出这条平行线和线段AE0,线段BE0的交点,并将这两个点的标签都设为点E,最后作出两种情况下的重叠部分的内部,就可以实现上述设想.至于点E0的位置确定,相信读者能自行解决.读者可以试试利用上述两种方法用几何画板软件作出下题中的重叠部分.
练习1:在Rt△ABC中,∠B=90°,BC=4,AB=8,D,E,F分别是AB,AC,BC的中点.P为边AB上的一个动点,作PQ∥BC交AC于点Q,以PQ为一边向右作正方形PQMN,作出正方形PQMN与矩形EDBF的重叠部分.
提示:此题可分为如图4所示的三种情况来设置.

图4
例2在▱ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从点A出发,以每秒1 cm的速度沿AB,BC向点C匀速运动,过点P作直线PM∥BD,PM与AD或DC交于点M.当点P运动1秒时,另一动点Q也从点A出发沿同样的路线、同样的速度运动.过Q作直线QN∥BD,QN与AD或DC交于点N.设点Q运动的时间为t秒(0≤t≤10),试用t表示直线PM与QN截▱ABCD所得图形的面积S.
点Q运动时,直线PM与QN截▱ABCD所得图形的面积有三种情况,如图5,6,7所示的阴影部分.要用几何画板软件画出此题的动态图形,如果不熟悉几何画板软件,会面临两个问题:一是如何在折线段ABC上作点P,并制作一个使得点P从点A连续运动到点C的按钮;二是不同情况下如何作出点Q.下面笔者就这两个问题的解决方法提供一些思路供读者参考.

图5
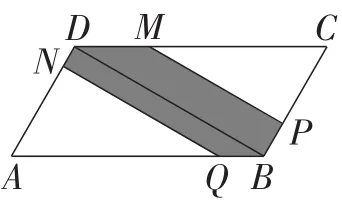
图6

图7
首先看第一个问题的解决方法,连接AC,在AC上作一点K,经过点K作BD的平行线,将此平行线和线段AB,BC的交点的标签都设置为P,与线段AD,CD的交点的标签都设置为M,这样就作出了点P,M.
如何作出点Q呢?为了便于读者理解,我们以五边形ABCDE为例介绍一下几何画板软件中“点的值”的概念.先作五边形ABCDE,再依次选中点A,B,C,D,E,执行命令“构造、五边形的内部”,选中该五边形内部,执行命令“构造、边界上的点”,设此点为P,选中此点,执行命令“度量、点的值”,这个值的意义就是当它从起点A出发沿着五边形的边界运动到某一处时,已经走过的路程和五边形周长的比值,根据这个比值就可以确定该点的位置.(注意:起点A是构造五边形的内部时,第一个被选中的点.)
练习2:正方形ABCD中,点E,F分别从点D,C同时出发,点E向C运动,点F沿着正方形的边CB,BA向点A运动,点F的速度是点E的速度的两倍,直线EF和直线AC交于点G.
(1)点F从点C向点B运动时,点G的位置会发生改变吗?试说明理由;
(2)点F从点B向点A运动时,点G的位置会发生改变吗?试说明理由.
综上所述,利用几何画板软件能画出由于点的运动形成的不同情况下的图形,必须综合利用几何画板软件的度量、计算、绘制点等功能来解决问题.其主要思路是:如果想让某种情况下图形的一个部分可见,而在另一种情况下这一部分不可见,那么可以将这部分图形和一个“后缀”是的值关联,这里的a是自变量x的临界值,利用这个值控制不同情况下的图形的显示和隐藏.另一种思路是将其中一条线段分成几段,其分界点就是图形的临界状态.
以上是笔者用几何画板软件制作涉及动点问题课件的一些心得体会,供读者参考.

