看图解题犯“糊涂” 分析求解获心得
徐海燕
(浙江省余姚市低塘初级中学)
作为教师,我们每天都在向学生传授新的知识,即使是复习课,也是要让学生温故知新,而作业或试卷是检验学生对每节课或每章节收效情况的最实在的标杆.在批阅作业或试卷的过程中,我们总会发现学生存在这样或那样的错误,细细思量这些错误,或许对学生的知识掌握情况会有新的感知,从而为教学积累经验,并采取适当的措施为下一阶段教学的展开做铺垫.下面笔者摘录几道作业题目和学生的相关解法,粗浅地和大家交流一下.
一、就图论题,草率下笔

图1
案例1:如图1,已知A,B,C,D是⊙O上的四个点.若∠ADC=
∠BCD=90°, 且AD=CD, 求证:AC⊥BD.
对于此题,学生出现了如下几种解法.
生1的解法:因为∠ADC=90°,AD=CD, ①
所以△ADC是等腰直角三角形.②
所以∠DAO=∠DCO=45°.③
又因为OA=OD, ④
所以∠ADO=∠DAO=45°.⑤
所以∠AOD=90°.⑥
所以AC⊥BD.⑦
生2的解法:因为AC是⊙O的直径,
所以∠ABC=90°.
又因为∠ADC=∠BCD=90°,AD=CD,
所以四边形ABCD是正方形.
所以AC⊥BD.
生3的解法:因为AO=CO,
所以BO平分AC.所以AC⊥BD.
这道题目比较简单,本以为学生稍微动下脑筋就可以做出,但上述解题思路,不禁让人眉头紧蹙.
生1在第①②步中的推理有根有据,乍一看,第③步似乎也言之有理,但细细深究,“∠DAC=∠DCA=45°”并不等价于“∠DAO=∠DCO=45°”.但学生从图形的表象出发,认为点O在AC上是默认的事实,无需特别说明;生2更是直接指明“AC是⊙O的直径”并加以应用,后面的步骤有条不紊,只可惜万事俱备,稍欠东风;生3视题目条件如不见,直接应用垂径定理的逆定理“平分弦(不是直径)的直径垂直于弦”,忽视了括号中特别强调的内容,只是就图论题,从始至终未指明“A,O,C三点共线”或“BD是⊙O的直径”.
教学启示:对于学生能直观感知题目中正确的数量关系或位置关系,教师要及时地给予肯定.但感知仅仅是解题的一个引子,重点还是在于后面的推理论证过程.而学生恰恰对推理论证的语言缺乏严谨性,逻辑思维不紧密.在教学过程中,教师要认真做好板书的示范作用,尤其是在学生初步接触几何证明题时,教师要培养他们养成推理论证时步步言之有“据”的习惯.
二、借图求解,缺乏深究
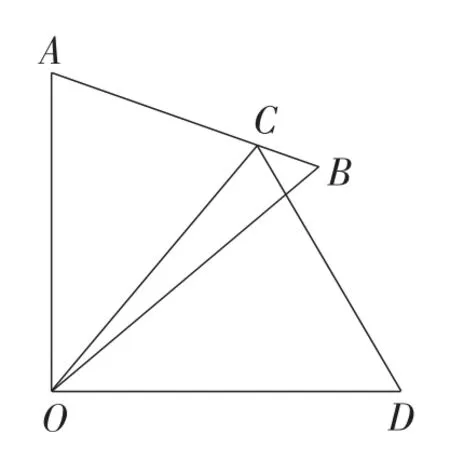
图2
案例2:如图2,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是_____.
答案:60°.
这道题目80%以上的学生都做对了,但从课堂反应来看,部分学生的“对”是因为借助了工具——量角器,单纯停留在填补卷面空白的基础上,不曾展开进一步的逻辑论证.在学生看来,在一些大型的考试中,如期中、期末或是月考,其中几何题的配图还是比较标准的.于是像选择题和填空题这样只需要写出最后结果的题目,学生在最后不会做的时候,就抱着侥幸心理填答案,课后也不再多加讨论.
教学启示:教师需要向学生传授一些解题技巧,如“特殊值法”“极限思想”,和类似上述借助数学工具求解角度问题等方法.但从另外一个角度思考,为了真正的体现题目的价值,在平时的教学过程中,教师仍应该要求学生对题目展开缜密的逻辑推理,不能有丝毫懈怠.与此同时,作为一线教师,平时需要多研究中考试题,筛选好题,挖掘其中的数学思想和求解规律,对学生“授之以鱼”的同时做到“授之以渔”,以便他们能“做一题、学一法、会一类、通一片”.
三、错得精彩,虽败犹荣
案例3:某地有一座圆弧形拱桥,桥下水面宽度为7.2 m,拱顶高出水面2.4 m.现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,此货船能否顺利通过这座拱桥?
学生解法:如图3,设y=ax2+2.4过点(3.6,0).
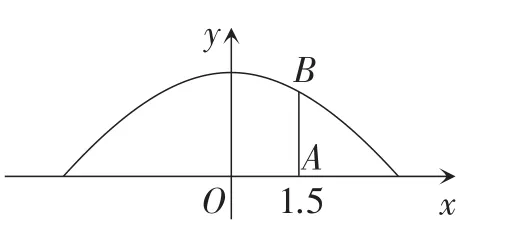
图3
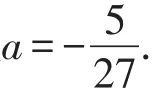
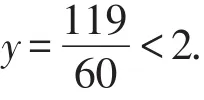
所以货船不能顺利通过这座拱桥.
有些拱桥问题可以抽象成抛物线问题,但必须有一个前提——题目中有明确说明,否则就仅仅是一己之见.而这道题目中只是说明它是一座圆弧形拱桥,所以只能通过构图的方式进行解题.即便如此,这位学生能够想到把拱桥抽象成抛物线,转换成代数问题,这一数学转化思想很好.所以在评语中,笔者对这位学生奉上八个字“错得精彩,虽败犹荣”.
教学启示:教学中,教师要换个角度看待学生所犯的错误,在错误中找到学生的闪光点,并给予肯定.与此同时,教师在解题教学中仍旧要向学生灌输利用代数方法解决几何问题的思想,关注习题的更新动向,精选用代数方法可以更好的解决几何问题的题目,让学生在解题中体验这一解题方法的独到之处.
四、依赖图象,忽视条件

图4
案例4:如图4,抛物线y=+c与x轴交于A,B两点(点A,B分别在y轴的左右两侧),与y轴的正半轴交于点C,顶点为D,已知A(-1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状,并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE,设△QPE与△CDB重叠部分(如图4中的阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
学生解法:(1)B(3,0),C(0,3 ) .
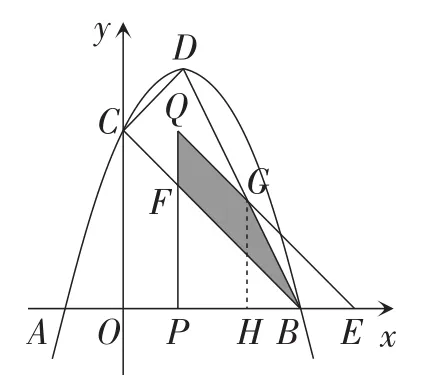
图5
(2)△COB为直角三角形,理由略.
(3)如图5,作GH⊥Ox,交x轴于点H,
其中直线BD的解析式为y=-2x+6,直线BC的解析式为y=-x+3.
所以QP=3,FP=3-t.
其中直线QE的解析式y=-(x-t+3)=-x+t+3.
令yQE=yBD,即-x+t+3=-2x+6,得x=3-t.
此时y=2t.
则HG=2t,HB=t,PH=3-2t,PB=3-t.

此题第(3)小题中点明“△COB沿x轴向右平移t个单位长度(0<t<3)”,尤其对t的范围进行了说明,求解中要求写出S关于t的函数解析式及t的取值范围,这无形中就是一种暗示,可惜很多学生没有看出来,对△COB的运动始末未做任何探究,直接从已有图形出发,求出四边形阴影部分的面积,一旦求出就作罢,殊不知这只是求出了运动的一个分支,还有另一个分支没有求出.事实上,如图6,当点Q恰好运动到BD边上时,重叠部分恰好由四边形QFBG转化成△QFB;如图7,当△QPE继续向右平移时,重叠部分仍为三角形,即△FGB.
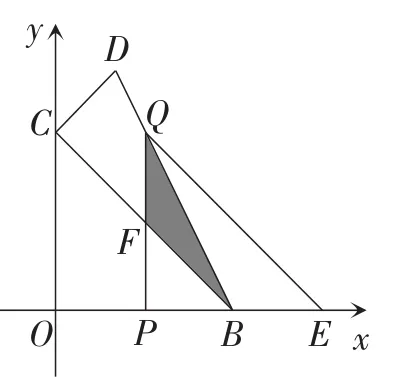
图6
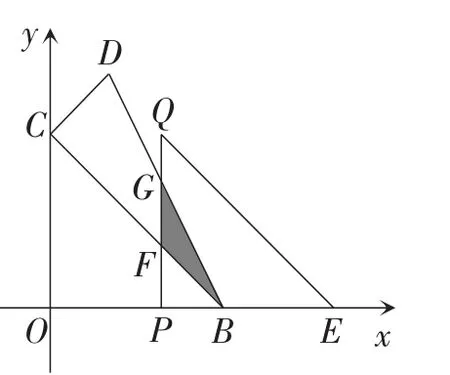
图7
教学启示:动点问题是初中数学中的一种常见题型.在解这类题目中,教师应该引导学生弄清楚图形运动的始末,尤其要注意运动中临界点的位置,让学生透过现象看清问题本质,在求解中体验数学中的表象美和内在美.
五、结束语
教学的步调一如既往地向前迈进,备课、授课、批改作业等依旧是教师每天的常规节奏.做个有心人,对学生作业或试卷中的答案不只是做对或错的评价,有时间还要多想想这些“解”的来由或背景,或许我们也会有新的收获.

