基于区间数信息的群决策逆判方法
陈 岩,李明月,曲家杰
(沈阳工业大学 理学院,沈阳 110870)
0 引言
自美国学者Saaty[1]提出层次分析法以来,群决策过程中专家的权重以及专家的决策水平就成为了决策研究领域的一个研究重点。群决策逆判方法(或逆判问题)就是评判群决策过程中各个决策专家的判断水平问题。关于群决策逆判问题,刘万里[2,3]采取方差分析以及相似关系、模糊传递闭包方法,给出群决策过程中AHP判断矩阵的逆判问题的分析方法。陈岩等[4,5]则通过改进的统计分析法解决了基于模糊互补判断矩阵和语言信息判断矩阵群决策逆判问题。针对基于模糊互补信息的群决策逆判方法,陈侠等[6]利用相对偏差给出了一种改进方法。此外,针对基于直觉模糊判断矩阵的群决策逆判问题,巩在武等[7]等利用相关度给出了分析方法。针对区间直觉模糊判断矩阵的群决策逆判问题,夏梅梅等[8]给出了基于相似度的分析方法。陈岩等[9]针对直觉模糊决策矩阵信息给出了基于相似度量的群决策逆判方法。
近年来,有关区间数不确定信息的排序以及群决策一致性问题研究取得了一些重要研究进展,而基于区间数不确定信息判断矩阵的群决策逆判问题研究工作所见甚少。本文首先将区间数的不确定偏好信息转换为互反判断矩阵,进一步利用方差度量分析方法对专家的评判水平进行判断、排序以及分类。最后用一个算例说明了这种方法的实用性和有效性。
1 基本概念和定义
为叙述方便,记N={1,2,…,n},M={1,2,…,m}。设在群决策问题中决策方案集为X={x1,x2,…,xn}(n≥2),xi为第i个决策方案;专家集为E={e1,e2,…,em}(m≥2),ek为第k位决策者。以下给出有关概念的简单描述。,其中元素表示方案xi对方案xj的相对重要程度,矩阵Ak满足:>0 ,
定义1[1]:设决策者ek针对方案集X给出了一个两两方案比较判断矩阵为,∀i,j∈N,称为互反判断矩阵。
定义2:设R为实数集,称闭区间[aL,aU]为区间数,用aˉ表示。其中aL、aU∈R,aL≤aU,分别为区间数的左、右端点。特别的,若 0<aL≤aU,则称闭区间[aL,aU]为正区间数。

定义3:设决策者ek针对方案集X给出的区间数评价向量为其中和为实数型数值,且
定义4:称直积X×X上的一个模糊子集P:X×X→为X中的模糊关系。
为叙述方便,设pij=up(xi,xj),pij表示方案xi与方案xj的重要性程度的比较,并规定:
(1)pij=0.5,表示方案xi与方案xj重要性程度无差别;
(2)0≤pij<0.5,表示方案xi没有xj重要,且pij越小,方案xi越不重要;
(3)0.5<pij≤1,表示方案xi比xj重要,且pij越大,方案xi越重要;
定义5:若比较判断矩阵P=[pij]n×n满足下列性质:
(1)pii=0.5
(2)pji+pij=1,∀i,j;i≠j
称矩阵P为模糊互补判断矩阵或互补判断矩阵。
定义6:若模糊互补判断矩阵P=[pij]n×n满足:
pik+pkj=pij+0.5,∀i,j,k
则称矩阵P是完全一致性的或是一致性互补判断矩阵。
2 区间数评价值与互反判断矩阵的转换
专家ek所给出的区间数评价信息向量,每个方案的评价值可以认为是一个区间,通过区间数比较[14]将区间数评价信息转化为两两比较的互反判断矩阵评价信息形式,记为其中:

在式(1)中,表示区间数优于区间数的可能度,即专家ek关于方案xi重要性优于方案xj的程度的评价信息,容易证明矩阵Q为互反判断矩阵。
3 基于区间数信息的群决策过程中专家逆判方法
3.1 正互反矩阵的特征向量的近似计算
求解正互反矩阵特征值、特征向量的和积法近似计算公式如下:
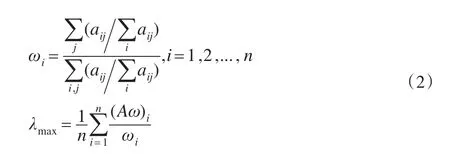
3.2 基于互反矩阵的数理统计分析
对于特征向量W=(ω1,...,ωn)T,由其构造的互反矩阵是完全一致的。然而在实际应用中互反矩阵A=(aij)n×n一般不具有一致性,因此互反矩阵A的元素与的对应元素之间关系由以下式子近似描述:

显然,当εij=1互反矩阵A是完全一致性的。
引理 1[1]:当δij∈(- 1,1) 时j=1,2...,n。其中C.I.为一致性指标。
定义 7:矩阵 ΔAk=[δkij]n×n称为矩阵A的偏差矩阵,
引理 2:若δij~N(0 ,σ2)(1 ≤i<j≤n)且相互独立,则
定理1:互反矩阵A是完全一致性的充要条件是χ2=0。证明:若互反矩阵A为完全一致性的,则,偏差矩阵 ΔA为零阵,即δij=0,易得χ2=0。反之,若χ2=0,则中的各项均为零,即δij=0,易得,由定义互反矩阵A是完全一致的。
如果互反判断矩阵Q为满意一致性的,由判断矩阵的一致性性质,那么χ2的样本观察值应当较小。进一步,可以视为度量决策者所做决策与一致性决策的偏离程度的统计量,其估计量越小,专家ek的评判水平就越高,因此,偏离度就可作为评判专家ek判断水平的一个标准。
通过计算的极大似然估计量,可以评价群决策决策专家们的判断水平,但群决策专家们实际评判水平差异是否显著仍需检验。
为叙述问题方便,设群决策中m位专家的方差估计量分别为,选用统计量,由假设检验理论可得如下结论:
根据该结论,可两两比较方差估计值检验决策专家的评判水平差异是否显著,方法如下,作假设检验:

取显著性水平α,若估计值则认为专家ek、ek+1处于同一档次;若估计值F>Fα,则认为专家ek的评判水平比专家ek+1评判水平明显高,即专家ek、ek+1评判水平不处在同一个档次上。经过两两比较可以将m位专家的评判水平分成若干档次。
3.3 逆判方法
根据前面的分析,基于区间数不确定信息的群决策逆判分析方法为:
(1)根据公式(1)将区间数评价值转换为互反判断矩阵;
(2)计算 ΔAk,k=1,2,…,m;
(4)对专家评价水平进行排序。越小,相应的评价水平越高;
4 算例
现设有六位专家 {e1,e2,e3,e4,e5,e6} 对四个方案其进行评判。其评价值以区间数形式表示,如表1所示。

表1 区间数
步骤1:由公式(1)将区间数评价信息转化为互反判断矩阵:
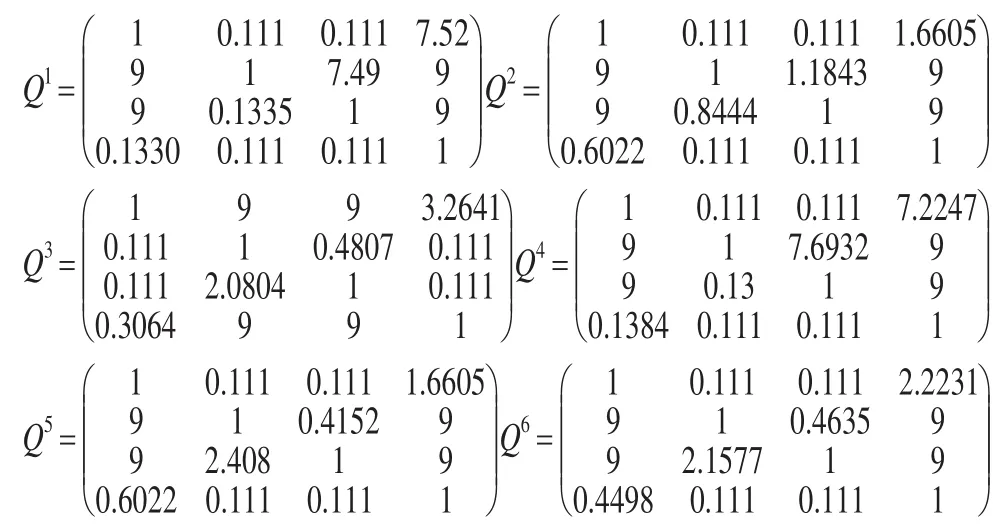
步骤2:由公式(2)用和积法求互反判断矩阵最大特征值、特征向量:


步骤3:计算偏差

步骤4:比较分类
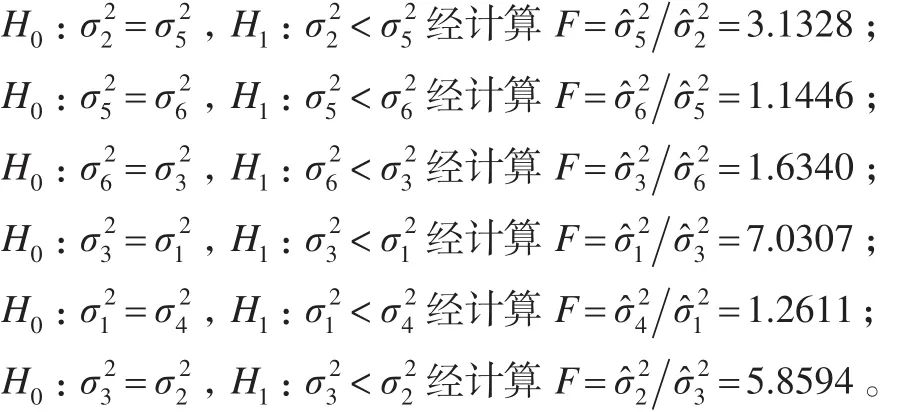
n=4,取临界值α=0.05=F0.05(6,6)=4.28。
由此可得e2评判水平最高,e5次之,e4评判水平最低,分类如下:(e2,e5,e6),(e3),(e1,e4)。
5 结论
针对基于区间数不确定信息的群决策逆判方法,本文通过方差估计量、假设检验方法给出了逆判问题分析方法。最后通过算例显示了该分析方法的有效性和实用性。该统计分析方法操作简单、易于掌握,为逆判问题进一步深入研究提供了一种有效的工具。

