拒绝服务攻击下的Euler-Lagrange系统的安全控制*

曹 然，程 龙

摘 要：研究了Euler-Lagrange系统在拒绝服务(denial-of-service, DOS)攻击其传感通信通道时的安全控制问题.为减少采样资源消耗，本文设计了基于事件触发机制的控制算法.针对DOS攻击活跃期和休眠期两种情况，设计了Lyapunov函数并证明了所提出的基于事件触发的算法能保证Euler-Lagrange系统在DOS攻击下的稳定性.最终通过仿真算例验证了算法的有效性.

0 引 言

近十年来随着控制技术以及通信技术的发展,将物理系统和信息系统结合设计的信息物理系统 (cyber-physical-system, CPS) 受到了越来越广泛地关注. 作为信息物理系统中的一个重要问题,其安全控制吸引了国内外学者的深入研究[1]. 安全控制问题主要研究当系统传感/通信网络受到恶意攻击时,攻击可能导致控制器无法正常接收到信息物理系统的状态信息,在这种情况下如何设计控制器并进行稳定性分析[2]. 安全控制问题具有许多实际应用,如考虑卫星网络或者大型供电网络在受到恶意攻击下,该系统能否保持正常工作状态.

根据攻击方式的不同,安全控制问题可分为拒绝服务(denial-of-service，DOS)攻击下的控制[3]和欺骗攻击下的控制[4]等情况;针对所研究的CPS系统模型的不同, 可分为一阶线性系统、二阶线性系统以及非线性系统的安全控制等[5-6].在现有研究中,通常先假设CPS系统模型符合输入输出稳定性,并结合相应性质分析出CPS系统状态在受攻击时不会发散,这种方法对系统模型要求较高[3,5]. 另一种方法将CPS系统分为受攻击时刻和不受攻击时刻两种情况,分别进行Lyapunov 稳定性分析,最后证明系统的整体稳定性,但这种方法目前只应用于线性系统之中[6-7].

本文研究了Euler-Lagrange系统的安全控制问题. Euler-Lagrange系统可以描述一类实际系统,如机械臂、无人机等[8].同时由于此类系统具有较强的非线性,也给控制算法设计带来了一定的挑战. 考虑到节省采样资源,本文选用事件触发思想设计控制器,控制器仅在事件触发时才会更新其控制输出[9].本文首先构建了辅助变量,然后根据Euler-Lagrange 系统的性质设计了控制器以及相应的事件触发律,并分别针对DOS攻击活跃期以及休眠期进行了Lyapunov 稳定性分析,并最终证明了在DOS攻击下的Euler-Lagrange系统的稳定性.

1 数学背景

本文研究的Euler-Lagrange系统由如下动力学模型描述[10]

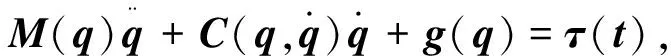
(1)

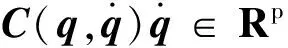
该模型具有以下三个性质[10]：

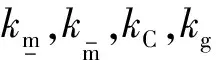
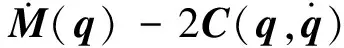
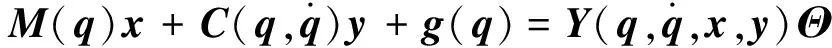
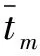
(2)

本文中采用的控制算法基于事件触发机制,控制输入仅当事件成功触发时才会更新. 用{tk}k∈N代表事件发生序列,则对于任意时刻t∈[tk,tk+1],理想控制输入为uid(t)=f(q(tk)). 在本文中,由于存在DOS攻击影响,控制输入在活跃期内无法更新,具体表现形式如下[12]

u(t)=f(q(tk(t)))

(3)

其中

(4)

本文中需要用到的定义和假设如下:

定义1. 考虑系统(1)在控制律(3)的作用下，若存在α,β∈R>0使得有

‖q(t)‖≤αe-βt‖q(0)‖

(5)

对于任意t∈R>0和q(0)∈Rp都成立, 则此系统是全局指数稳定的.

假设1[5]. 对于DOS攻击时间段Ton,其满足条件

‖Ton‖≤T0+t/τa

(6)

其中T0,τa为正常数.

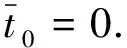
假设2[12]. Euler-Lagrange系统动力学方程(1)中的矩阵M,C,g中的元素都是相对于系统状态q(t)全局Lipschitz 连续的. 此类方程符合一大类实际物理系统.

2 控制算法设计

定义如下辅助变量[13]

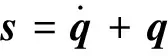
(7)

由性质3可得

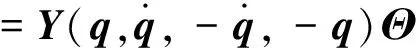
(8)

设计事件触发控制算法如下

τ(t)=-ks(tk)+Y(tk)Θ,t∈[tk,tk+1]

(9)

式(9)中k为正的常值控制增益,tk为之前定义的事件触发时间,同时事件触发时间由事件触发律决定, 触发律形式如下

k1‖q‖+‖ε‖+k‖e‖≥λk‖s‖，

(10)

式(10)中k1为正的常值增益,具体的定义将在之后给出,λ∈(0,1),e(t)=s(tk)-s(t),

ε(t)=[Y(tk)-Y(t)]Θ. 当式(10)成立时,事件触发,控制器更新其状态.

注2. 目前大部分相关研究可分为两种,即(1)关注符合输入输出稳定的线性或非线性系统在拒绝服务攻击下的安全控制问题和(2)采用事件触发控制的Euler-Lagrange系统在未收到拒绝服务攻击下的安全控制问题. 而暂未有考虑拒绝服务攻击下Euler-Lagrange系统的安全控制问题研究,这也是本文创新点所在.

将式(7)～(9)代入式 (1) 中得

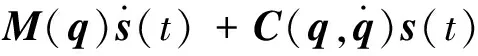
=-ks(tk)+[Y(tk)-Y(t)]Θ.

(11)

针对提出的基于时间触发机制的控制器(9),本文有定理如下:

定理1. 当假设1和假设2成立时, 对于Euler-Lagrange系统(1), 在DOS攻击满足τa≥(kw2+kw1)/kw1(kw1,kw2将在之后给出)的情况下,本文设计的基于事件触发的控制算法(9)可使得系统全局渐近指数稳定.证明.

选取如下 Lyapunov 候选方程

(12)

对上式求导，有

sT[Y(tk)-Y(t)]Θ+k1(s-q)Tq

=-ksTs-ksTe+sTε+k1(s-q)Tq.

(13)

首先考虑未受DOS攻击的时间段Toff, 在此时间段内触发律(10)不成立. 记此段时间内的 Lyapunov 函数为V1, 从式(13)有

≤-k‖s‖2+k‖s‖‖e‖+‖s‖‖ε‖+

k1‖s‖‖q‖-k1‖q‖2

≤(λ-1)k‖s‖2-k1‖q‖2

(14)

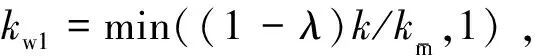
(15)

考虑第二种情况，即受 DOS 攻击的时间段Ton. 记此段时间内的 Lyapunov 函数为V2, 从式(10)有

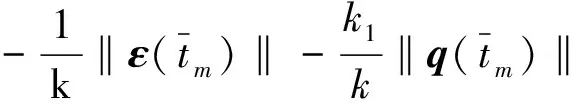
(16)

从e(t)的定义中可得到

‖e(t)‖≤‖s(tk)‖+‖s(t)‖.

(17)

将式(17)带入式(16)中可得

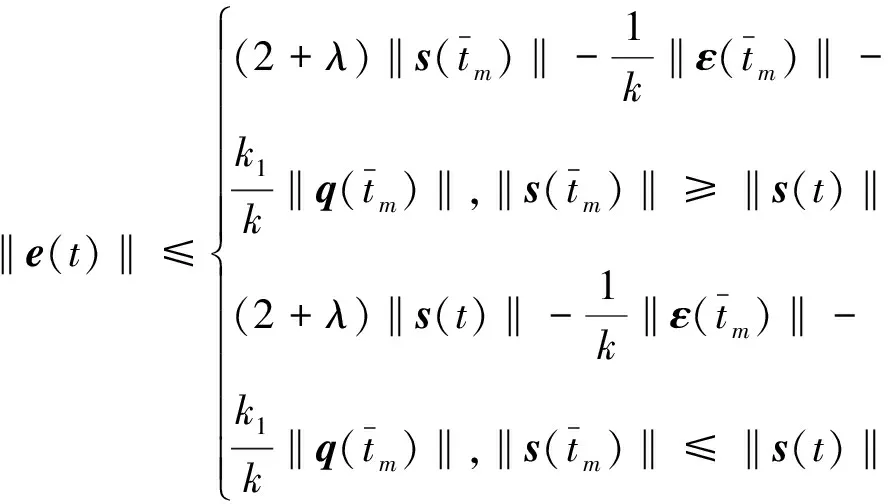
(18)

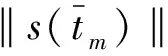
k1‖s‖‖q‖-k1‖q‖2

≤(λ+1)k‖s‖2+‖s‖

‖q‖-k1‖q‖2.

(19)

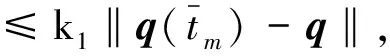
(20)

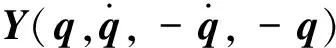
≤(λ+1)k‖s‖2+2k1‖s‖‖q‖-k1‖q‖2

≤(λk+k+k1)‖s‖2

≤kw2V2(t),

(21)

(22)

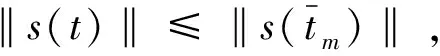
(23)

合并式(22)和(23),并考虑到y=ex-x,x∈[0,∞)为严格增的函数,可得

(24)

最终合并系统受到 DOS 攻击和未受到 DOS 攻击的情况, 可以得到

(25)

≤…

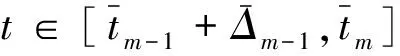
≤e-kw1|Toff|ekw2|Ton|V(0).

(26)

≤…

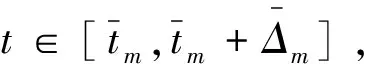
≤e-kw1|Toff|ekw2|Ton|V(0).

(27)

综上可知,对于t∈[0,∞),总有

V(t)≤e-kw1|Toff|ekw2|Ton|V(t0).

(28)

考虑到

-kw1|Toff|+kw2|Ton|

=-kw1(t-|Ton|)+kw2|Ton|

≤-kw1t+(kw2+kw1)(T0+t/τa)

≤(kw2+kw1)T0+[(kw2+kw1)/τa-kw1]t.

(29)

将式(29)代入(28)最终可以得到

V(t)≤αe-βtV(0)，

(30)

其中α,β分别为α=(kw2+kw1)T0,β=kw1-(kw2+kw1)/τa. 从式(30)可推得

‖q(t)‖2≤αe-βtV(0)/k1

≤α′e-βt‖q(0)‖2,

(31)

其中α′=α‖V(0)‖2/(k1‖q(0)‖2).

显然如果τa≥(kw2+kw1)/kw1,系统是全局渐近指数稳定的. 关于系统中无Zeno现象的分析,由于文章篇幅限制,在此不再赘述.

3 仿真验证

本节通过仿真算例来验证所设计的控制算法的有效性. 考虑一个二连杆转动机械臂所构成的系统,机械臂的动力学由Euler-Lagrange方程描述. 在仿真实验中, 所采用的二连杆机械臂的各杆质量分别为m1=2.5 kg和m2=1.8 kg;各杆长度分别为l1=1.0 m和l1=0.6 m;各杆连接点到质心的距离分别为lc1=0.5 m和lc2=0.3 m;各杆转的动惯量分别为J1=0.2083 kg·m2和J1=0.054 0 kg·m2;重力加速度为g=9.8 m/s2.

机械臂的初始关节角度为[2.00 -1.50]Trad,同时初始转动角速度为 [-1.25 1.10]Trad/s. 控制参数选择为k=5,k1=1,λ=0.9. 相应的有τa≥6.83,仿真中选择τa=7.50, 符合条件.

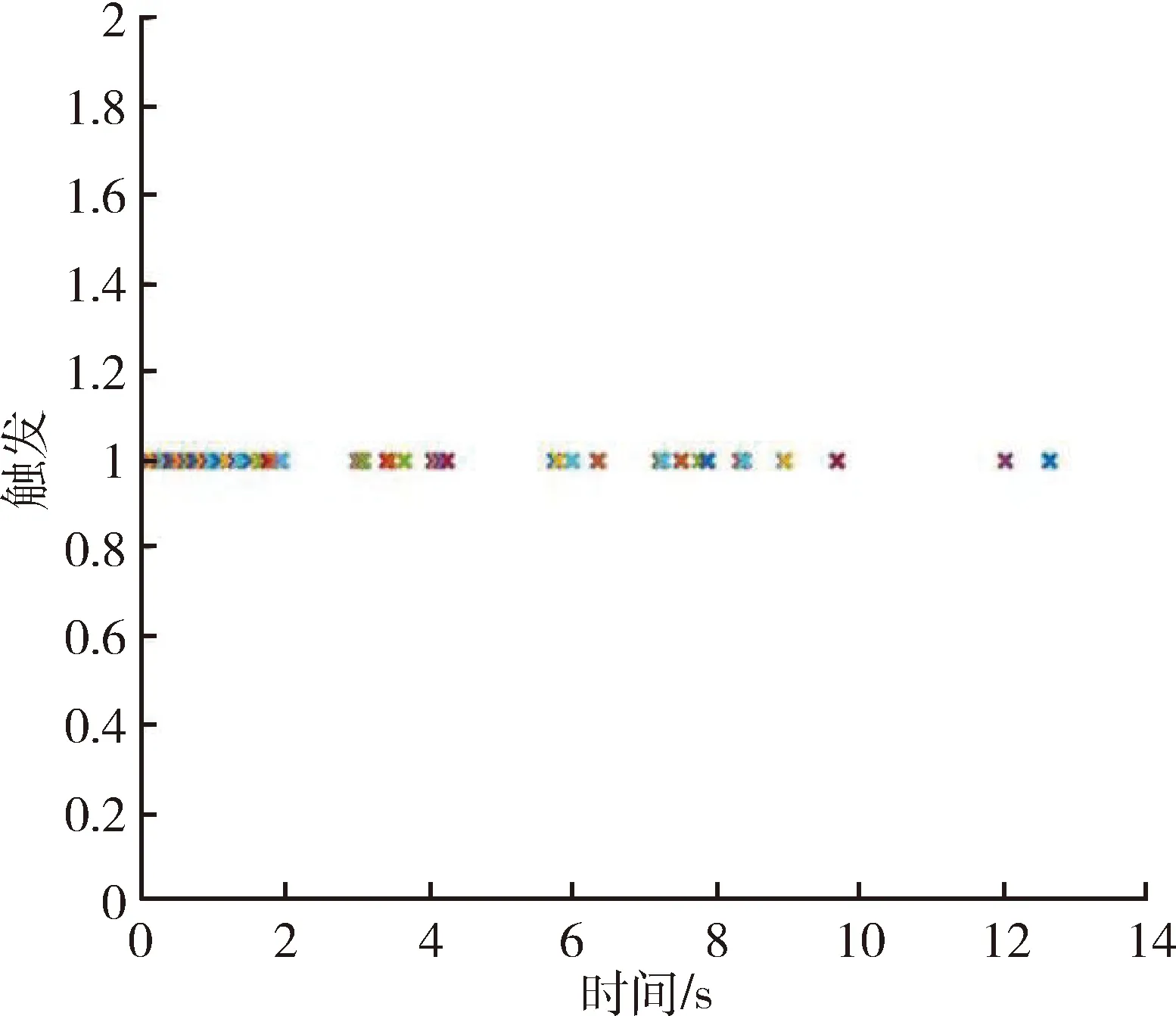
图2 当k=5时的事件触发时刻Fig.2 Events triggered times when k=5

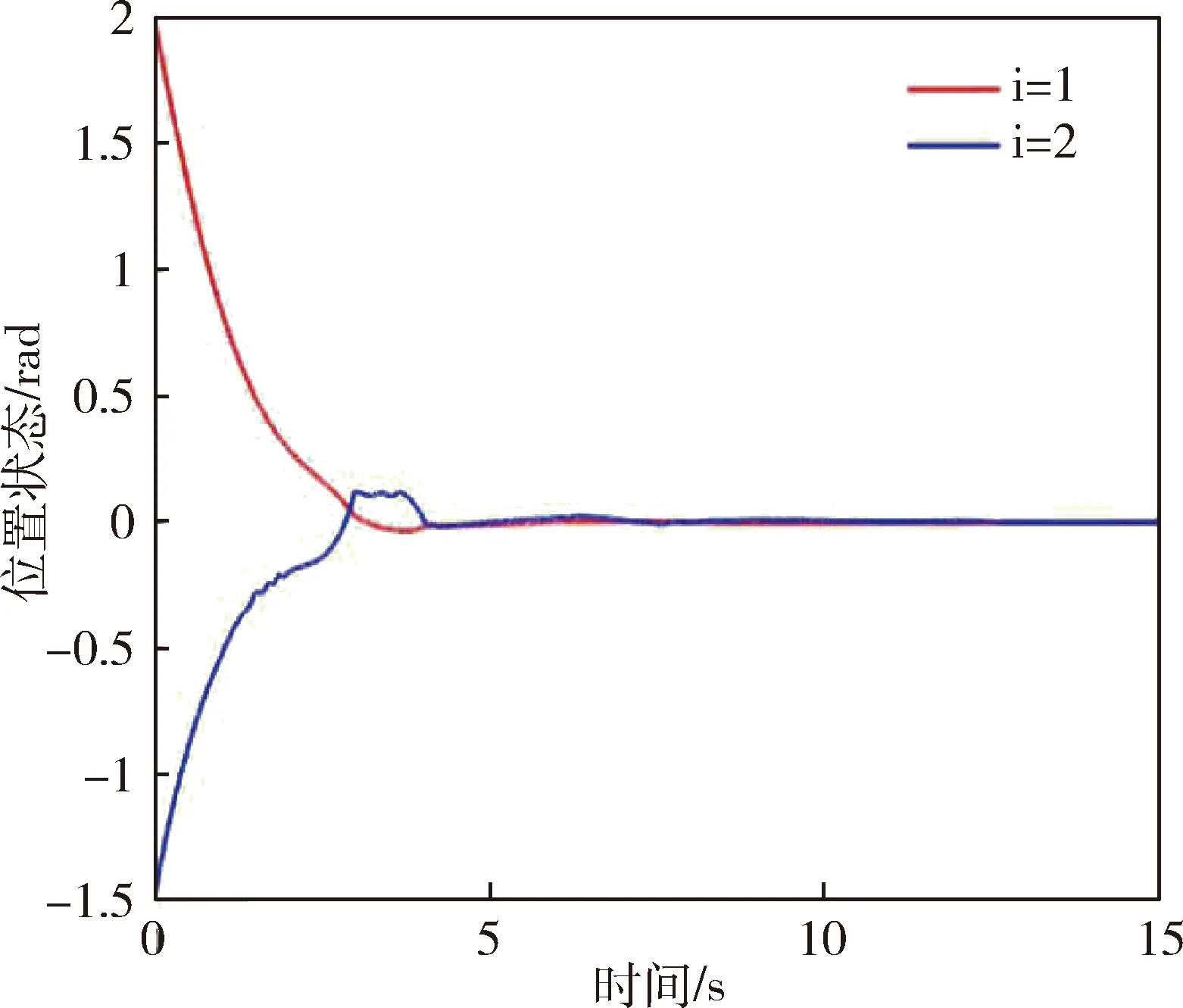
图3 当k=5时的系统位置状态信息Fig.3 System’sposition when k=5

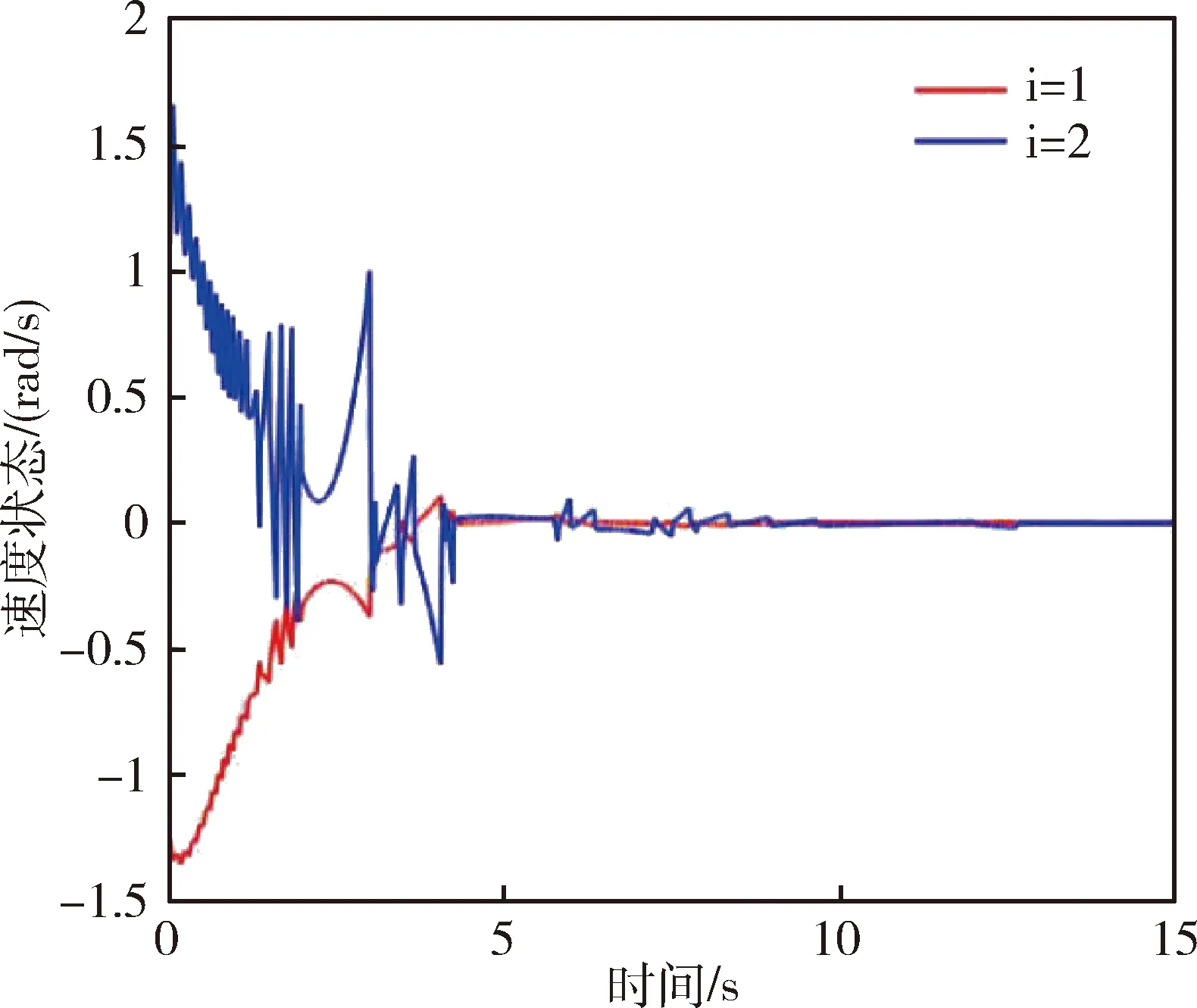
图4 当k=5时的系统速度状态信息Fig.4 System’s velocities when k=5

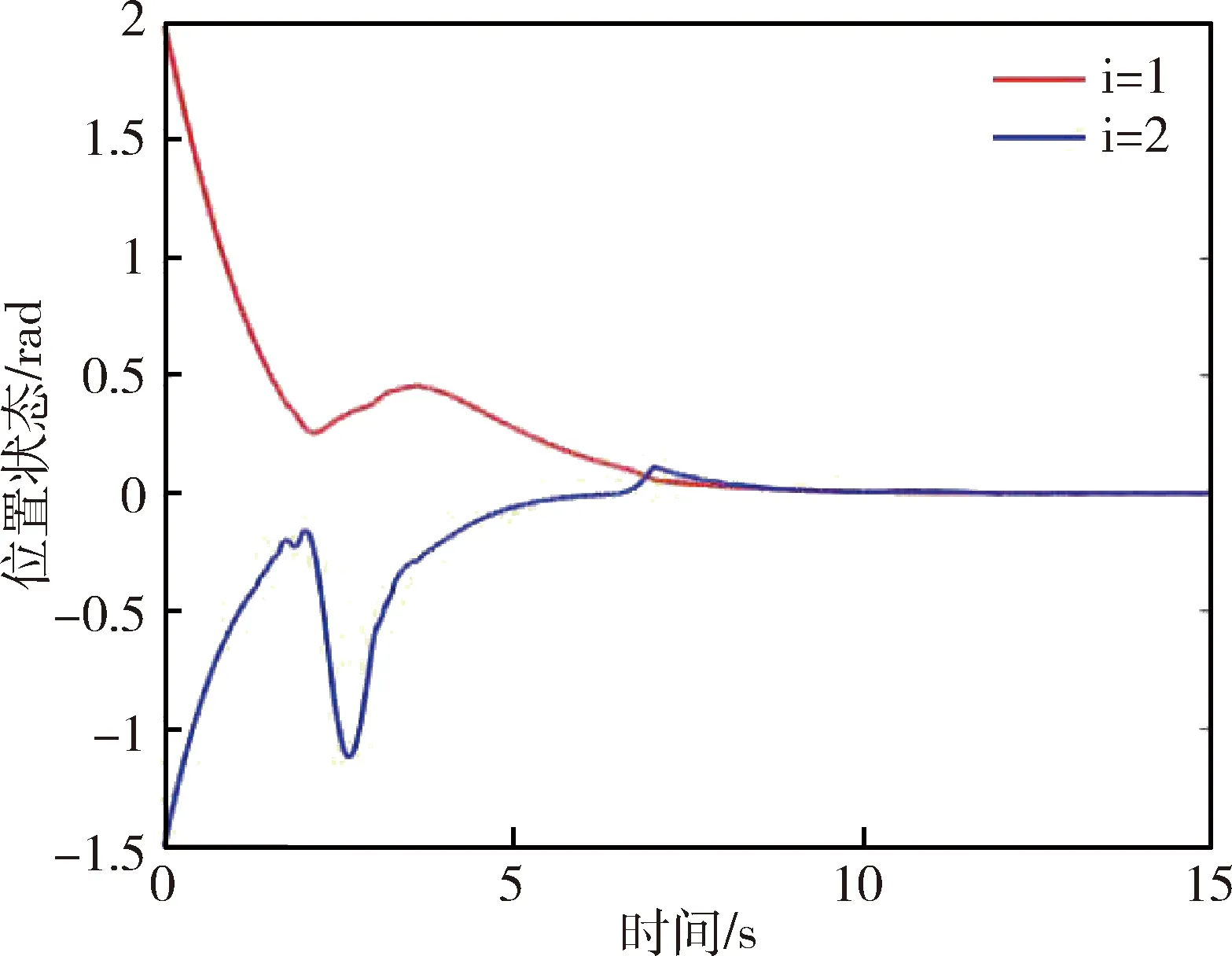
图5 当k=3时的系统位置状态信息Fig.5 System’s position when k=3

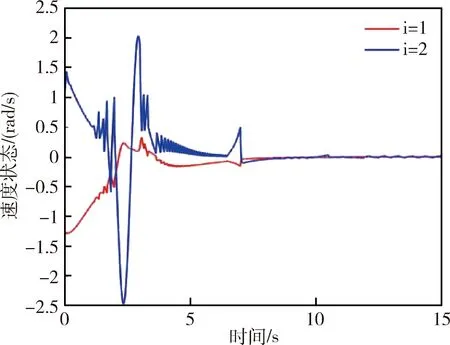
图6 当k=3时的系统速度状态信息Fig.6 System’s velocities when k=3

仿真中模拟的DOS攻击时刻如图1所示,事件触发时刻如图2所示,系统位置状态信息变化如图3所示,系统速度状态信息变化如图4所示. 若改变控制参数为k=3,其他参数不变. 从仿真中可看出,在所设计的事件触发控制算法驱动下,即使受到DOS攻击,系统误差依旧趋于稳定,但减小控制增益会降低系统响应速度.

4 结 论

本文主要考虑了 Euler-Lagrange 系统在DOS攻击下的安全控制问题. 控制器的分析思路主要通过引入辅助变量构建状态方程,并结合一些常用的假设给出了针对DOS攻击时长的约束条件. 考虑到采样资源有限,本文提出了一种基于事件触发机制的控制算法,分析了DOS攻击的活跃期和休眠期两种情况,并证明了控制算法在一定条件下可以使Euler-Lagrange系统维持指数稳定. 最终结合二连杆机械臂系统给出了相应的仿真分析验证了理论分析结果.