浅谈二次根式的分母有理化

（渭城区第二初级中学 陕西咸阳 712000）

二次根式的除法运算，通常是先写成分式的形式，再化去分母中根号的方法来进行的，即分母有理化。分母有理化是初中数学运算中的一个难点。许多学生在进行分母有理化时由于不注意方法、技巧，使得运算过程不但繁琐，而且易错。那么，分母有理化有哪些方法和技巧呢？现举例说明，供大家参考。

一、乘以分母的有理化因式

解法的关键是准确判断分母的有理化因式。两个含有根号的代数式相乘，如果它们的积不含有根号，那么这两个代数式互为有理化因式。的有理化因式是的有理化因式是，的有理化因式是，的有理化因式是。

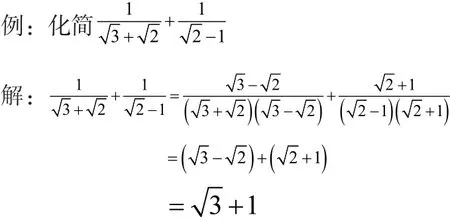
二、约分法

将分式的分子、分母适当分解因式，约去分子、分母的公因式，再分母有理化。

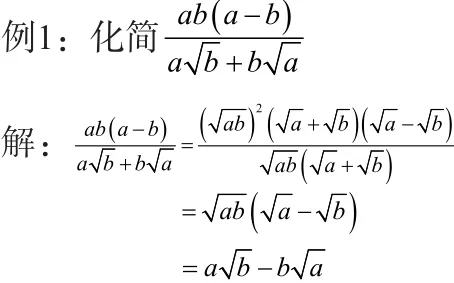
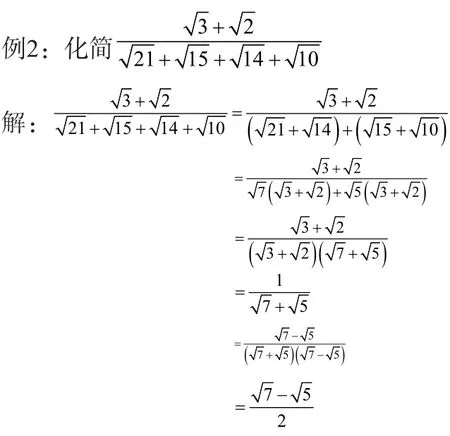
三、换元法

运用整体思想，通过设元，换元，将不熟悉的问题转化为熟悉的问题，复杂的问题转化为简单的问题，从而用熟悉或简单的方法来解决问题。

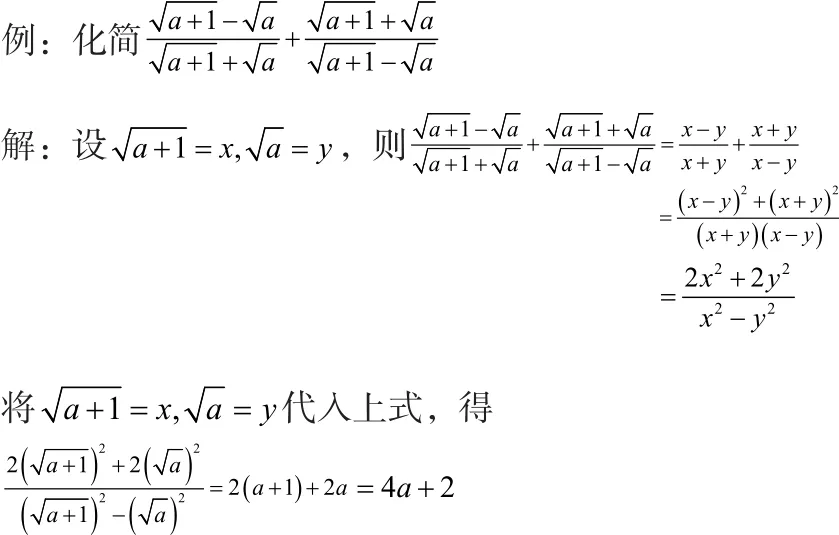
四、拆项法

拆项是关键，做题时要善于观察、分析，从而找到解题最佳途径。

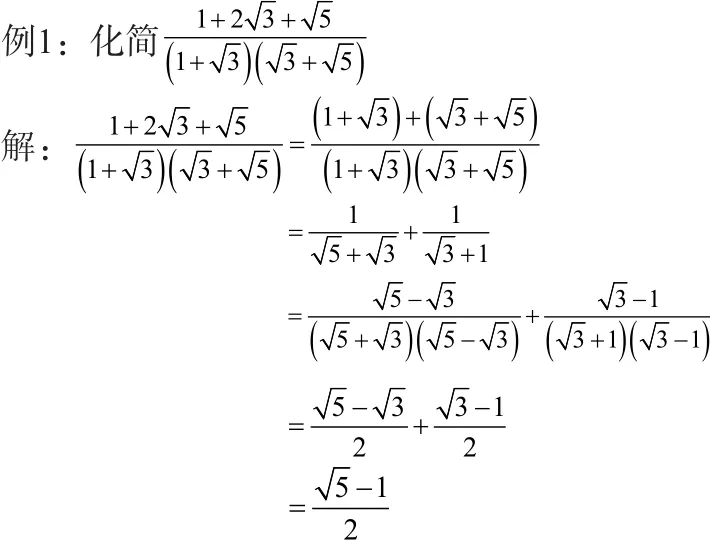
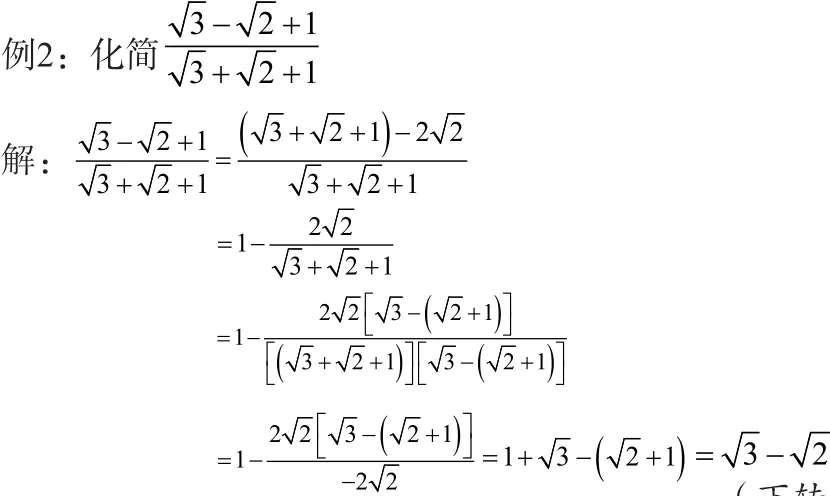
五、通分法。

象异分母分式加减一样，先通分，再分母有理化。

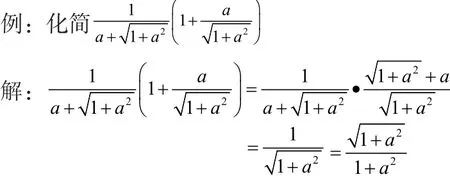
六、倒数法

对分母比较复杂的分式化简时，可以先将待化简的二次根式取倒数，再化简，最后进行回归还原。

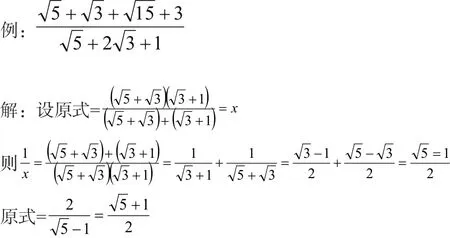
结语

贝尔特说过：“良好的方法能使我们更好地运用天赋的才能，而拙劣的方法则可能阻碍才能的发挥。”数学方法是数学的核心和灵魂，二次根式的分母有理化除掌握常用方法外，还需根据不同题的特点，灵活应用解法，讲求技巧，这样才能化繁为简，化难为易，使问题得以顺利解决。