参透动点轨迹，等效转化破解——2018年淮安市中考第27题的思路突破与反思

☉江苏省海安市曲塘中学附属初级中学 戴 路

平面几何中存在一类较为特殊的问题，即几何动点问题，该类题一般以点动为基础，考查学生问题分析、条件转化、原理利用的能力.本文将以2018年淮安市的一道几何压轴题为例对其问题形式及解法原理展开探究，以期对师生的学习备考有所帮助.

一、试题呈现

（2018年江苏淮安中考卷第27题）如图1所示，在平面直角坐标系xOy中，一次函数的图像与x轴和y轴分别相交于点A和B，动点P从点A出发，在线段AO上以每秒3个单位长度的速度向原点O作匀速移动，到达点O后停止运动.点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN，设运动时间为t秒.

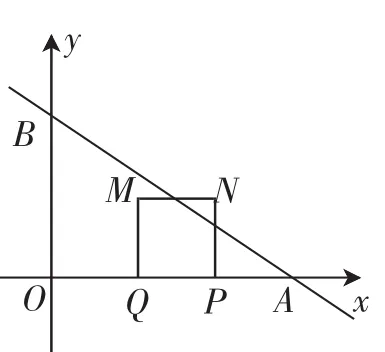
图1

（2）在整个运动过程中，设正方形PQMN与△AOB的重叠部分的面积为S，试求S与t的函数表达式；

（3）如果正方形PQMN的对角线的交点为T，请写出运动过程中OT+PT的最小值.

二、思路突破

（1）求点Q的坐标实际上就是求线段OQ的长.首先需要明确图中的点、线之间的关系.由于A和B为一次函数与坐标轴之间的交点，因此A、B两点均为定点，（ ，），（ ，），即 、 均为定值点 运动，而点A60B04AOBO.P Q是点A关于动点P在x轴上的对称点，则可以理解为AP=QP，且长度随点P的运动而变化，分析可知OQ=AO-APQP=AO-2AP，当时，AP为定值，，则OQ=6-2=4，即点Q的坐标为（4，0）.

（2）正方形PQMN是以边PQ向上作的正方形，由于PQ的长度随着点P的移动而变化，因此正方形PQMN的大小也是变化的.设正方形PQMN与直线的交点为 和 ， 与 的重叠部分的形状与点 的DCPQMN△AOBP位置相关，其面积的求解需要结合动点移动，并采用面积割补的方式来获得.由于点P的移动，会造成MQ相对于y轴的位置及几何形状发生变化，总体可概括为三种情形：①MQ位于y轴的右侧，且重叠部分为五边形；②MQ位于y轴的左侧，重叠部分介于五边形与四边形之间；③MQ位于y轴的左侧，重叠部分为梯形.根据运动时间t可以求得点P的坐标为（6-3t，0），点C的坐标为（6-3t，2t），则线段，下面分别进行讨论：

情形1：MQ位于y轴的右侧时，时间t的取值范围为0≤t≤1，此时的重叠部分的形状为五边形，如图2所示，其面积可以表示为SDMQPC=SMNPQ-S△DCN，可得SDMQPC=

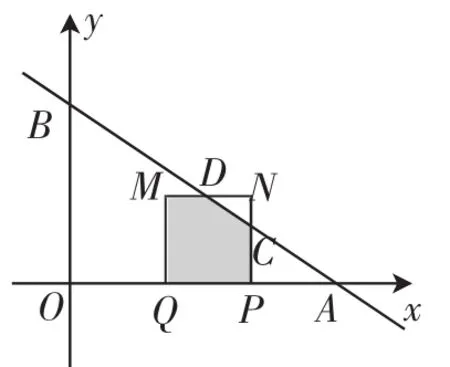
图2

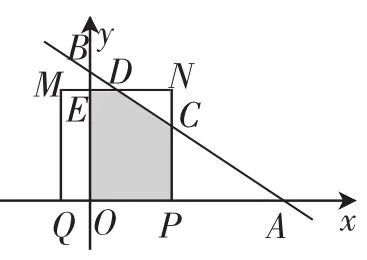
图3

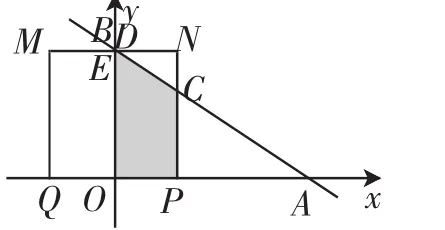
图4

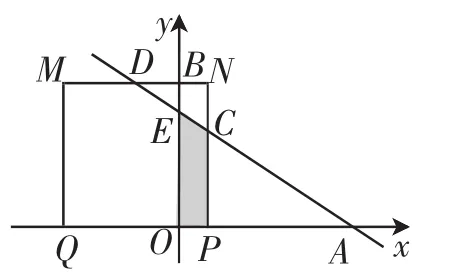
图5

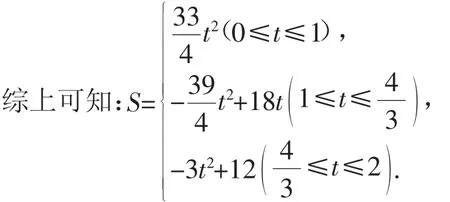
（3）本小题求OT+PT的最小值，由于点T会随着点P的移动而移动，因此其长度之和也会随之变化，可以从研究动点的轨迹入手，确立OT+PT取得最小值时的具体情形.由于TP=TN，因此可以通过求OT+TN的最小值来获得，在整个运动过程中都有NP=PQ=AP，则运动过程中形成的△APN为等腰直角三角形，即∠NAP始终为45°，可进一步将其理解为：点N的运动轨迹为点P围绕A点顺时针旋转45°，因此点N的运动轨迹为与x轴呈45°的直线，如图6.

OT+PT的值可以看作线段OT加上点T到直线AN的距离，求解最小值可以利用“两点之间，直线最短”原理，即点O、T、N三点处于同一直线上时OT+TN取得最小值.分析可知，只有当点Q与原点O相重合时，才能确保点O、T、N共线，如图7，此时△NQA为等腰直角三角形，OA=6，

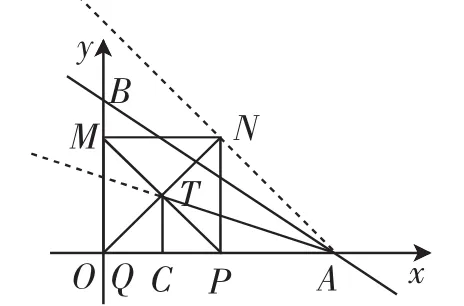
图6

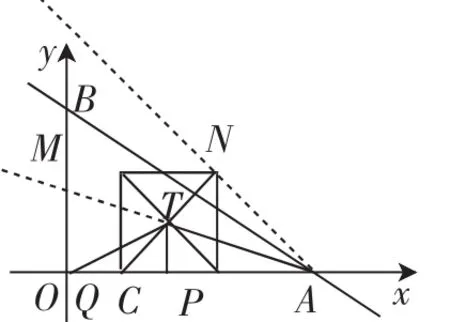
图7

三、评析拓展

本题目属于典型的几何动点问题，问题设置涉及了点坐标的确定、动态几何面积求解及线段最值，是动态几何中常见的题目，在问题形式和解法上存在以下特点：

1.联动性

上述考题中由于点P的移动使得几何线段长发生变化，进而使得正方形的大小发生变化，从而产生了几何重叠面积、线段最值等问题.其形式上是以点动为驱动，联动线、面研究，由特定问题分析发展到动态几何研究，是几何三大元素点、线、面的完美融合.

2.等效性

上述考题的第（3）问是整个问题的核心.求解的突破口是研究点的坐标及动点的轨迹，而坐标系中的正方形是最为关键的参照，既可以利用其性质研究边长，也可以结合其对角线的交点确定动点的移动轨迹.整个解题思路是建立在线段等效思想之上，即通过研究点的运动轨迹对线段长进行等效转化，最后利用两点之间直线最短原理确定线段和的最小值.

无论是在问题的联动形式上，还是解法的等效上，在近几年的中考中均存在同类型题，下面以2017年的广州题为例进行对比探析：

考题：（2017年广州市中考卷第24题）如图8所示，矩形ABCD的对角线AC、BD相交于点O，△COD关于CD的对称图形为△CED.

（1）求证四边形OCED是菱形.

①求sin∠EAD的值.

②如果点P是线段AE上一个不与点A重合的动点，连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，然后以1.5cm/s的速度沿着线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所用时间最短时，求AP的长和点Q走完全程所需要的时间.

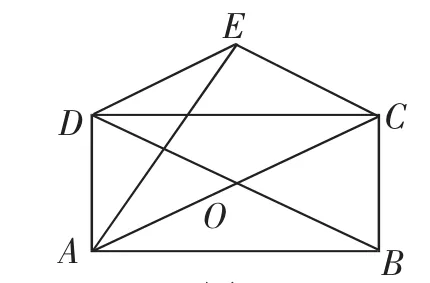
图8

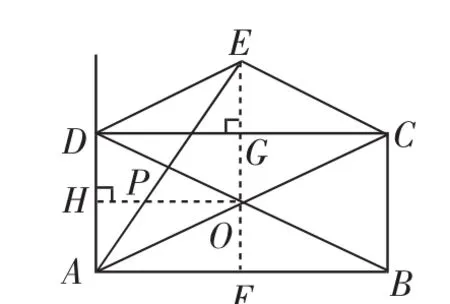
图9

解析：本问题同样为几何动点问题，下面主要分析第（2）问②，点Q的全程路线长为OP+PA，则用时，则PH=的最小值可以转化为求OP+PH的最小值.显然只有当三点共线，且OH⊥AH时才能取得最小值，如图9，易得O

上述考题形式上是求运动时间最短，但考虑到速度一定，因此首先可以转化为线段与数的比值和，然后通过线段等效的方式转变为三点之间线段和的最值问题，最后利用“三点共线距离最短”原理完成求解.本问题的解法核心同样是线段等效，共线求最值，所不同的是在对线段等效时结合了三角函数，而第一道考题则是研究动点运动过程中的线段关系，这两种方式都是求解线段最值问题的常用思路.

四、反思学习

1.把握问题特点，理清解法思路

几何动点问题的形式是多样的，涉及几何的点、线、面等内容，但从本质上来说还是点的运动问题，无论是直角坐标系中的动点，还是普通几何上的动点，认识问题特点都需要结合点的移动，明确动点个数、运动路径、运动速度及联动形式等.在明确问题特点的基础上，建立起“点动—线变—形变”的联动体系，然后通过分析点的运动，确定线段的变化情况，并采用等效转化的方式分析线段的最值，一般对于线段最值的研究可以采用几何转化和建立代数方程两种方式，前者主要用于一般几何体系中，后者可以用于坐标体系中.

2.关注数学本质，重视原理学习

几何问题的学习应该从其本质上进行，如上述考题关于最值的研究实际上就是对点的运动轨迹的分析，求值思路也是基于对线段的转化，然后利用三点共线完成.对于几何问题的求解，应包括对问题形式的认识，以及对解法本质的理解，尤其是三点共线取最值，其理论依据是“两点之间，线段最短”.因此，对于几何动点问题，应充分认识问题本质，理解解法的基本原理，必要时可结合直观的几何图像，通过几何证明的方式完成，将学习重心由问题表象分析转移到解法本质探究上，从而形成较为系统的解题策略.

3.学习思想方法，拓展解题思维

数学学习的内容主要有两方面：一是知识内容的理解；二是解题方法的掌握.前者属于基本的学习要求，后者属于能力层面的提升，是数学学习的核心.而对于解题能力的提升仅仅依靠题海战术是无法实现的，也无法真正掌握解法的精髓.解题能力的提升首先需要学习解题的思想方法，理解解题过程中的指导思想，如上述采用的等效转化思想；其次是掌握基本的解题思路，提升自我的解题思维.对于思想方法的学习，可以结合典型考题，如数形结合思想可以结合数学函数考题，构造思想可以结合几何类考题.结合考题理解方法的优势所在，掌握思想方法的指导意义，从而掌握方法的精髓所在，拓展解题思维.

五、写在最后

关于几何动点题，中考的典型题较多，考查形式也多种多样，但始终离不开对于点的运动分析，线段长度的等值转化，不同的解题策略会带来不同的解题效果，但正因其变化形式的不确定性使得该类问题成为中考独具魅力的一道风景.深入探究考题，形成解题思路，充分发挥考题的指导意义，促进思维的提升是考题学习的价值所在.