对一道课本习题的变式教学

☉合肥师范学院数学与统计学院 洪 倩

“变式教学”指的是教师有目的、有计划地对例题、习题进行合理转换.合理转换问题的条件或结论，保留问题的本质因素，从而使学生更好地掌握问题的本质属性.下面是对课本习题进行的变式教学设计.

题目：（沪科版七年级上册数学角课后习题）如图1是中央电视台部分节目的播出时间，确定钟表上时针与分针形成的最小的角的度数.

思路：求时针与分针所形成的最小角，实际上求7到12之间所形成最小角度.

解析：时钟被分成12等份，即每一大格：360÷12=30°，则5×30°=150°.

图1

一、条件一般化，问题不变

变式1：求7：20时，分针和时针形成的最小角.

解析：分针每分钟转30÷5=6°，时针每小时转一大格30°，即每分钟转30÷60=0.5°.因此，题中的时针与分针形成的角度由两部分组成，即4到7的角度与时针超过7的部分的角度.

答案：3×30°+20×0.5°=100°.

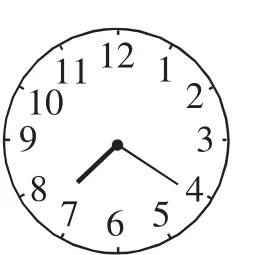
图2

变式2：求7：50时，分针和时针形成的最小角.

解析：此题中的时针与分针形成的角度由两部分组成，即8到10的角度和时针实际位置与8相差的角度.为了方便计算，一般情况下采用：7到10的角度减去时针超过7的角度.

答案：3×30°-50×0.5°=65°.

变式1与变式2与原题的区别在于当分针不指向12点时，时针指向的不是整点数，在计算时针与分针的最小夹角时，需要考虑时针与整点数的偏角.变式1考查的是分针在时针后面的情况，变式2是分针在时针前面的情况.

图3

二、条件与问题互换

变式3：分针在时针后面，7点多少时，时针与分针的最小夹角成100°？

解析：相对于之前的给定时间求角度问题，这是给定角度求时间问题，时针与分针的夹角由两部分组成，即4到7的角度与时针超过7的角度.

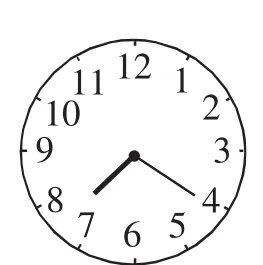
图4

答案：设x分钟时，时针与分针的最小夹角成100°，则有7×30-6x+0.5x=100，解得x=20.

变式4：7点多少时，时针与分针的最小夹角成100°？

解析：此道题除去限定条件，需要分两类情况进行解答：分针在时针前面、分针在时针后面.第一类情况与变式3解法相同，第二类情况时针与分针的最小夹角由7到10的角度减去时针超过7的角度，即求出时针超过7所形成的夹角，便可求出时间.

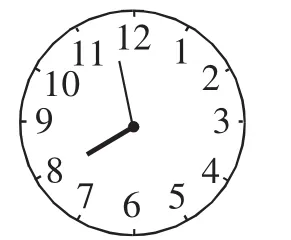
图5

答案：分针在时针前：7×30-6x+0.5x=100，解得x=20.

变式3与变式4都是给定角度求时间问题，变式3有“分针在时针后面”这一限定条件，因此只需考虑一种情况，变式4未给定限定条件，需要考虑两种情况.条件与问题互换，有利于培养学生的逆向思维及分类讨论意识.

三、问题特殊化

变式5：当前时间为7：20，再过多长时间时针与分针第一次相遇？

解析：这道题实际上是上一个变式问题的特殊化，即时针与分针的夹角成0°.

答案：设7：x时，分针和时针第一次相遇，则有6x-7×30-0.5x=0，解得（分钟）.

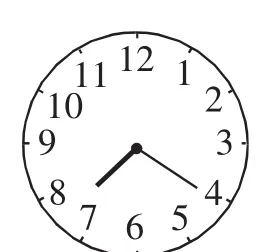
图6

［这道题是钟表内的相遇问题，也可以利用相遇时间=路程÷速度和来解决，路程是一开始时针与分针相差的路程即时针与分针的最小角度，速度和是时针的速度与分针的速度之和.

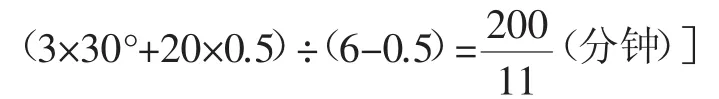
变式6：当前时间为7：50，再过多长时间时针与分针第一次重合？

解析：分针在时针的前面，需要注意的是时钟是顺时针转动.

答案：设8：x时，时针和分针第一次重合.

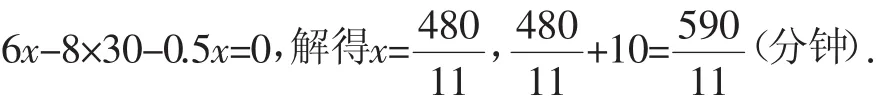
变式7：当时间为7：20时，至少过多长时间，时针与分针在一条直线上？

解析：此类问题需要考虑两种情况，时针和分针在同一条直线上，一种情况是时针与分针重和，另一种情况是时针与分针的夹角成180°，再比较哪种情况的时间短.此题，明显时针、分针第一次重合时时间较短，时针、分针在一条直线上.

图8

变式8：当时间为7：50时，至少过多长时间，时针与分针在一条直线上？

解析：此时，很明显由观察得时针与分针第一次成180°时，时间较短，时针与分针在一条直线上？

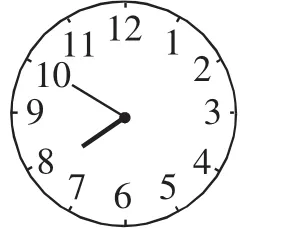
图9

变式5和变式6都是时针与分针第一次相遇问题，是变式3、4的特殊化，即时针与分针的夹角为0°，区别在于变式5是分针在时针的后面，变式6是分针在时针前面，要考虑到时针、分针的转动方向，否则易出错.变式7和变式8需要考虑到分针、时针在同一条直线的两种情况.

在涉及钟表中的角度问题时，条件和问题是变动的.这时需要的是把握三个着手点：作图、时针和分针转动顺序、时针和分针每分钟转动的角度，把握这三个不变因素，就相当于抓住钟表中角度问题的本质，无论条件、问题如何变动都可以解决它.

课本例题、习题都是教材编写者精心编写的，课外辅导资料也是以课本习题为依据编写而成的，时钟问题是数形高度结合的范例，结合了形象思维和逻辑思维，是培养学生分析问题、解决问题能力一个很好的平台.因此，教师在扎根课本的同时，理应进行由浅入深的变式教学，通过改变条件或问题拓展学生的思路，提高学生的思维品质.