论数学教师的教学过程观——对作为课程目标的“过程与方法”的思考

☉淮北师范大学数学科学学院 张 昆

列为数学新课程“三维目标”之一的“过程与方法”目标，究竟指什么？我们可以对“过程”与“方法”两者进行单独分析.这里的“方法”一词作为课程实施中的教学目标是明确的，是指通过教学活动，学生在掌握知识的同时，从产生知识的背景中获得所使用的“方法”，这种“方法”可以迁移到应对未来可能面临的具有相似结构的新问题中去.因此，“方法”作为一项课程或教学目标是准确的，也是一线教师可以理解的，进而可以转化为他们教学设计时有意识地思考与实现的目标.那么，“过程”一词在教学目标体系中意指何物？人言人殊，林林总总，不一而论.本文将从作为课程目标的“过程”与“目标”本身这两个词的字面意义展开讨论.

一、作为课程目标的“过程与方法”的字面上的释义

作为课程或教学目标的“过程”与“目标”本身的意旨究竟是什么呢？《现代汉语词典》第五版（2010年4月河北第406次印刷）在第525页，将词条“过程”释义为“事情进行或事物发展所经过的程序”；在第971页，将词条“目标”释义为“射击、攻击或寻求的对象”或者“想要达到的境地或标准”.如果就词典上关于“过程”与“目标”这两个词的字面意义上来分析的话，“过程”与“目标”两者之间存有内在矛盾，是“过程”，就不能是“目标”，反之亦然.如此，“过程”就不应该作为课程（或教学）目标体系中的“目标”加以阐述与认同.进一步的理由如下：

其一，不论教师采用何种手段进行教学活动，其呈现的总是教师的教与学生的学两者相结合、统一于课堂上的某种活动序列之中，即呈现于一种师生在课堂上进行活动的“过程”，因而这种“过程”就没有什么特别之处.因为，无论教学活动的成败，它都一定会呈现出某种过程，因此，有的教学“过程”可能有利于在学生掌握知识的同时，实现知识隐藏的教育目标；而有的教学“过程”只能使学生机械地发生知识（如死记硬背、强化训练等），不能实现教学具有教育性的目的，后者这样的“过程”如果作为课程或教学目标，与需要实现的知识教育价值的目标岂不是南辕北辙？这有可能会对教育造成灾难性后果.

其二，教学目标是教学所追求达到的某种具有正面价值的“境地或标准”，它就是一种“终点”，达到此处，说明教师的教与学生的学已经完成了，教学活动已经结束，接下来，需要就教学新内容重新建立某些新的目标，进行新的任务的教学.因此，“目标”就一定不是“过程”，课程目标只能是在课程实施的教学活动过程中实现的.由此分析可知，“过程”作为课程目标体系中的“目标”就是将结果与产生这种结果的活动“过程”混淆了.事实上，将“过程”写入课程目标可能是课程设计者为了矫正我们传统教学重结果、轻过程的教学活动现实，而加以强调提醒教师注意的手段，但是，却不能矫枉过正，把不能作为“目标”的“过程”当作了“目标”，由此可能造成课程目标的价值损失.

其三，这个“过程”到底是教师的教学“过程”呢？还是学生的学习“过程”呢？亦或是教学“过程”与学习“过程”两者的某种整合呢？我们很难将其区别开来.实现课程目标的重要途径是在课堂教学中，通过教师与学生的共同活动，经历这一过程，学生的身体与精神达到了某种有价值的“境地或标准”的结果（附带的结果是教师形成了教学经验，掌握了教学技能，获得了教学能力，即所谓的“教学相长”，但是，这些有关教师发展的价值，是一定不能作为课程目标的，因为课程目标是单项值地针对学生正面发展的美好结果而言的），而教师只能作为促进学生达到目标的手段（对于实现课程或教学目标来说，教师只是作为促进学生发展的工具），因此，教师的教学过程一定不能作为教学目标，否则，就会混淆手段与目的的区别，从而视手段为目的.

如果从这几个方面来理解作为课程目标的“过程与方法”的话，这种设置课程或教学目标时提出的目标形式不仅概念模糊，而且存在明显的矛盾与逻辑漏洞.事实上，我们听了大量（在职教师与高年级高师数学师范生）基础教育的数学课（或数学说课），就某个知识点的教学，教师在设置教学目标时都是采用了“三维目标”的表述形式，其中，在对“过程与方法”这项目标的表述中，他们的用语一般为“通过对二次三项式的因式分解的探究过程，使学生掌握‘配方法’分解因式的方法”；或“通过对三角形内角和的结论证明活动的探究过程，让学生体悟作辅助线的某种思考方法”；或“通过对数轴定义的建构活动过程，让学生体会数轴‘三要素’的次第发生及其配置而成的系统，使每一个有理数都可以在某条直线上找到相应的精确位置来表示，由此促进学生理解‘数形结合’方法的涵义”，等等.

在这些例子中，我们都可以明显地看出，“目标”与“过程”是一种“目的”与达到目的的“前提”之间的关系（“过程”甚至不能作为达到“目标”的“手段”，只能说是“前提”，“手段”是由教师的教学设计形式与结果转化成的课堂上的教学活动），“过程”不是达到目标的“手段”，更不可能是“目标”本身.正如演戏，需要剧本、演员、舞台等要素；演戏的目标在于实现它的社会意义与价值（“化民成俗”），“剧本”与“演员”是承担这种价值的手段，而“舞台”只是一种“前提”条件，至于“舞台”是豪华的还是简略的，其实对演戏的目标而言，不起决定性的作用；教学中的“过程”就可以用演戏中的“舞台”类比之.

在教学中，达到教学目的（目标）总是离不开教学活动过程的（甚至达不到某项目标的教学也一定会出现某种活动过程，因为，任何知识的演化总会形成一种过程），因此，教学活动过程只能是达到教学目标的前提，而达到教学目标的手段是教学方法的选择，这种教学手段的实现的关键支点就是启发学生获得形成知识结论所需要的作为问题的外显信息的“方法”，就是在确定的、结论性的知识结构出现之前，知识结构中内含的元素（信息）应该首先呈现出来，但其形式在大多数情况下可能是杂乱无章的，需要教师带领学生组织信息，由这种杂乱无章的信息组织、生成知识结构，这种组织信息活动过程所产生与使用的“工具”就是“方法”，对于数学而言，这种伴随知识发生所使用的“方法”就是教学方法，它当然可以作为课程或教学所要实现的目标之一.

二、作为课程目标的“过程与方法”的意蕴分析

由此可知，如果从字面意义上来说，“过程与方法”中的“过程”的内涵意义是不可能作为课程或教学目标的，“方法”可以.因此，我们在设置课程目标体系时，要么去掉“过程”这一项要素，使“过程”这个词条不进入课程目标体系，如果一定要使“过程”进入课程目标体系的话，就要使“过程”或者“过程与方法”这一整体成为一个专有概念，否则，就一定会出现使作为目标的“过程”或“过程与方法”形同虚设的一种“标签”式的不良后果，成了一纸空文，即在现实的课堂教学活动中，无论教师如何努力，这项目标总是不能实现的，反之，也可以说，无论教师如何不努力，这项目标却是一定会实现的，这就产生了一种悖论.在分析“过程与方法”列为基础课程的三维目标之一时，有学者指出，“完全混淆了整个教学论体系中的教学目标、教学过程与教学方法之间的逻辑关系”.

实际上，它混淆了学生通过学习掌握知识的目标，并基于知识发生的同时，隐含的许多教育性目标的要求，学习过程甚至于教学过程之间的区别.“过程”是知识结构还未形成，而是作为信息的具体元素处于动态的、正在向生成结构（发生知识）形态前进的途程中，而“目标”是静态的、在主体的设想中，已经由具体的元素生成最终结果的（客观存在的）形式，并且就教育而言，伴随这一知识结果的出现，学生的优良精神品格得以形成.由此可知，一般情况下，“过程”不是目标本身.因此，我们必须对作为教学目标的“过程与方法”中的“过程”概念作出特别的限制，使它成为一个专有名词，进而形成专有概念，才有可能作为一项具体的课程目标提出来，使之具有现实的意义.

为了研究“过程”是如何演化成课程目标的，我们首先摘引靳玉乐先生的有关基础教育课程目标的论述，“基础教育课程目标的表述方式有三种：行为目标、展开性目标和表现性目标.与它们三者相对应的可以表述为：知识与技能、过程与方法、情感态度价值观.过程与方法适用于展开性目标表述，注重的是了解学科研究的过程与方法，因此导引学会发现问题、思考问题、解决问题的方法，学会学习，形成创新和实践能力等”.对于行为目标与表现性目标，我们容易理解，行为目标在作为标准（如布鲁姆的目标评价体系）的评价中也会比较好地得以落实，唯有展开性目标难以理解，因为目标是某事物发展完结的终点，一种终止的状态，它既然还在展开中，就是说，目前还没有达到某种终止的状态，它们还在向终点迈进，那它如何又能作为课程目标呢？

依据靳先生的论述，我们发现，这涉及的其实是课程设计者在向教师提出课程实施的教学建议，建议他们采用充分揭示、暴露或展开知识教学活动的过程，如“提出问题、思考（分析）问题与解决问题”的活动序列，引导学生自己从中生成相关的方法，以此形成学生的更为深刻的精神品格，使用这种方式进行教学设计，通过这一途径实现“方法”的教学目标（当然，知识的掌握；技能的获得；能力的形成；观念的生成、积累、酝酿与再生；个性与品格的发展等也是在这一过程中实现的），由此，使教师立足于教学过程，形成并且习惯于利用如此的“教学过程观”，以指导教师教学活动的展开，使学生经历知识、基于知识的形成，产生方法、观念、优良的心理品格等的过程.

因此，课程目标体系中的“过程与方法”目标，可以理解为两者具有内在关联性的整体（其实是作为一个名词使用，而不是并列地意指两项对等的事物），其最终目标是“方法”，而“过程”则是通过并依靠教学活动过程产生“方法”，即“方法”才是真正的目标，而“过程”是产生具体方法的学习或教学手段经历的途径，两者合二为一，体现出了一种辩证的统一.只有这样，从学理上说，作为课程目标的“过程与方法”才可以说得过去.由此分析，我们知道课程目标的“过程与方法”层次意旨在于，在课程实施的过程中，教师通过教学设计，促进学生在掌握具体知识的同时，感悟与体验知识的形成过程，这其中一定隐含着发生知识的某种方法，从而实现“过程与方法”的统一，只有这种统一的整体（即“过程与方法”作为一个词素）才能作为课程目标体系中的一项目标.

如此，就“过程”而言，乃是课程设计者对教师作出的重要建议，通过建议促进教师在教学活动中形成“教学过程观”，就是说，教师在教学设计及其在课堂上的展开，自始至终都不要忘记设计出有价值的教学“过程”，学生是基于、通过、凭借、依靠这种有价值的“过程”实现“方法”目标的.对此，王策三先生指出，“在教学过程中，把概念、原理、公式等简单地呈现给学生，学生简单地直观，如照镜子、录音、录像，或如物体挪动、植物移栽那样，这的确是不行的”.这些就是单纯传授知识和简单传授知识（是一种无价值的“过程”）的突出体现，在（特别是传统）教学现实中，大多数情况下，正是教师的这些教学行为活动（“无价值的过程”）方式，损伤了数学知识的教育价值.

三、体现教师教学过程观决定教学过程形式的教学设计示例

由此分析，我们发现，作为专有概念的课程目标体系中的“过程与方法”目标的实现，就是试图启发学生经历知识的发生、发展与形成过程的长长的序列，学生从这种教学活动序列中体悟解决问题的方法的产生过程，它的本质是决定教师的课程实施，教师通过教学设计所选择与施用的展开过程.只有处理好教学过程中现实的、本真的教师的教与学生的学的活动过程与教学方法，“过程与方法”（终极是“方法”）的课程目标才能在现实中得以实现.教师在教学设计中所要处理的过程与方法来源于两个不同的层面，实践上，是对知识的认识，理论上，是经由哲学过程观的指导，只有如此，才能彰显教师教学设计的意义与价值，产生良好的教学效率与效果，最终体现在课堂上教师教学行为活动过程之中.

就行为哲学而论，人的行为总是在自己的某种观念指导下进行的（除了条件反射的应急情况），也总是在某种目的引导下进行的，而这种观念与目的最终来源于他对所面临的问题信息与作为知识结构的结果的认识与理解，即实践与认识活动的共同作用.同时，由于教师的教学是有计划、有意识的极具针对性的活动，而且具有历史传承性与现实借鉴性的条件，因此，教师也就有可能会利用自己经验中的或观摩他人实践中的某些有效观念自觉指导自己的行动（而不是时时事事都得从具体的外在问题信息中生成指导活动的观念，即来源于教师自己亲身实践所形成的观念）.因此，指导行为的观念也可以分为“撷取现成的观念”与“即兴生成的观念”两种形态，而前者最终又是由后者经过长期实践检验为正确的，并且在大脑中酝酿转化而来的.

在作为专有概念的“过程与方法”课程目标的实现中，基于知识的发生所使用的特定方法（参照教师对学生掌握特定知识所必不可少的心理活动环节及其过渡性中介的认识.因为，当学生掌握具有某种特定性质的知识时，首先，知识所内含的特定内容与掌握方式，就以改造了的形式转化为个性经验的一部分.这些内化了的知识经验，不仅成为一种认识、实践的工具和能力，而且内含着教育性的价值，如精神品格的形成，道德品质的提升等），教师可以选择合适的教学方法，通过教学设计的处理，这种教学方法就可以转化为课堂上师生的活动形式，而课程活动形式是由教师教学预设活动形式决定的，教学过程形式又是由教学过程决定的，教学过程来源于教师的教学过程设计，最终来源于教师观念的指导，即教师教学过程观的指导.我们看一个平面几何证明题的教学设计的例子.

如图1，在△ABC中，∠ADC＝∠BAC ①.求证：∠CAD＝∠CBA ②.

师：请用不同标识在图1中标示出所求结论与已知条件中各已经存在的一对相等角.

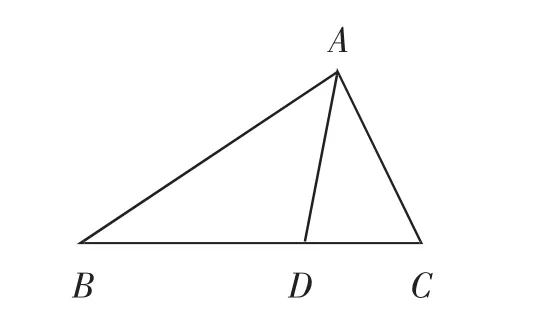
图1

生1：已知条件∠ADC＝∠BAC中的∠BAC被线段AD分割开来，图形的重叠影响了探索问题思路的展开.我想，首先解决重叠问题，使我们容易看清图形的本质，……

师：这是一个好的指导操作行动的建议！大家动手试一试.

学生活动关键环节实录：首先把图1中的△ADC平移出来，得到了图2与图4，其次，根据已知条件∠ADC＝∠BAC ①和要证明的结论∠CAD＝∠CBA ②，把图2变换成图3的位置形态.经由此项分离图形的活动结果在黑板上的展示，全体学生都成功地运用不同的标识标示出了图1中的这两对相等角（就学生活动的成果，教师精心地在黑板上作出相关的图形，并调整图形呈示的位置）.

师：非常好！现在，请对比图4与图3，你有新发现吗？

生2：比较图3与图4中这两个三角形之间角的关系可得（相机板书）：

已知条件是∠ADC＝∠BAC ①，

所求结论是∠CAD＝∠CBA ②，

还有公共角∠ACD＝∠BCA ③.

图2

图3

图4

生3：分析条件与图形的特点，可知，在这三个等式中，①和③成立，②是要求证的结论，应该成立，但是……

师：其他同学还有什么想法？

生4：我想，应用“三角形的内角和等于180°”这个定理.

生5：①②③三个等式左边的三个角是△DAC的三个内角，右边的三个角是△ABC的三个内角.于是，我们把这三个角的等式左、右两边分别相加，就能得到这两个三角形各自的内角和，它们都等于180°，即：

∠DAC＋∠ADC＋∠DCA＝180°，

∠ABC＋∠BAC＋∠ACB＝180°.（相机板书）

师：精彩！下一步怎么想？

生6：由于这两个等式的右边相等（180°），从而，知道∠DAC＋∠ADC＋∠DCA＝∠ABC＋∠BAC＋∠ACB ④.于是，只要将④的左、右两边分别对应地减去①与③的左、右两边，就可得到结论②也成立了.

这个课例就是将证明思路的精确表达（即这个例子的教学活动的结果“证明”中将条件与结论“逻辑链接”——环节及其联接中介）的过程转化为教师指导学生通过分析活动，获得思路（产生“逻辑链接”的心理环节及其过渡性中介的构建）的过程，这两种过程是笔者在不同教学过程观的指导下所选择（或产生）的不同的在课堂上实施的教学行为，两者对实现知识的教育价值的作用大相径庭，迥然有别.它是笔者数学教学过程观横跨二十多年时间演化的结果.

四、简要结束语

基础教育课程的“三维目标”体系中的“过程与方法”目标，就其字面意义而言，其中的“过程”是不能作为目标的，因此，“过程与方法”只能作为一个专有概念进入目标体系，它的主旨是课程设计者提醒课程实施者（一线教师），强调要通过教学（特别是学生学习的）活动过程使学生自己发现解决问题（组织外在信息形成知识结构）的方法，从而，将“过程”与“方法”辩证地统一起来，作为一个专有概念.通过课例，我们发现，这种整合统一的专有概念是有价值的，由此作用，使教师最终形成了教学过程观，它对发挥知识教育价值有着极具针对性的指导作用.