关注基本图形 渗透数学思想——对一道七上期末统考压轴题的命制与思考

☉浙江省海盐滨海中学 姜黄飞

笔者有幸承担了2018年嘉兴市七年级上学期期末统考卷的命制工作，现将其中第26题（压轴题）的命制过程及思考与各位同仁分享.

一、命题立意

作为七年级上学期期末统考的压轴题，以关注初中数学核心知识和数学思想为前提，关注数学核心素养，要有一定的区分度，能够反映出在思维上的较高要求；又想改变2016、2017年连续两年对线段上动点问题的考查，改变一下压轴题的试题背景，呈现一定的新意.综合整份试卷的知识点的分布和思想方法的考查，制定双向细目表，确定压轴题以学生熟悉的一副三角板为素材，着重考查学生动手操作的实践能力与数学基本素养，在问题解决的过程中突出考查角的和差、角平分线、一元一次方程等七年级核心知识点的应用，同时关注分类讨论、方程思想等的考查.

二、命题过程

笔者将一副三角板如图1所示放置，使得OA与OC在同一直线上，先固定三角板COD，将三角板AOB绕着点O顺时针旋转，在旋转的过程中，OA、OB、OC、OD其中的一条边所在直线均存在平分另两边组成角的情况，可以选取其中的一条用作命题的素材，既可以考查学生的动手操作，又可以考查分类讨论的数学思想，同时在旋转过程中，∠AOD、∠BOC等角度大小随着旋转在发生变化，可以研究它们在变化过程中存在的较特殊的关系，同时存在分类思想，这也可以用作命题的思考点，基于以上的思考形成一稿.

一稿：26.（8分）如图1，一副三角板中各有一个顶点在直线EF的点O处重合，三角板AOB的边OA和三角板COD的边OC与直线EF重合，∠AOB=45°，∠COD=60°.

（1）则图1中∠BOD的度数是多少？

（2）如图2，三角板COD固定不动，若将三角板AOB绕着点O顺时针旋转一个角度α，在转动过程中当OB平分OA、OC、OD其中的两边组成的角时（两块三角板都在直线EF的上方），求可能出现的所有情况的α的值；

（3）若将三角板AOB绕着点O顺时针旋转一周，请直接写出OA所在直线恰好平分∠COD时∠AOE的值：_____.

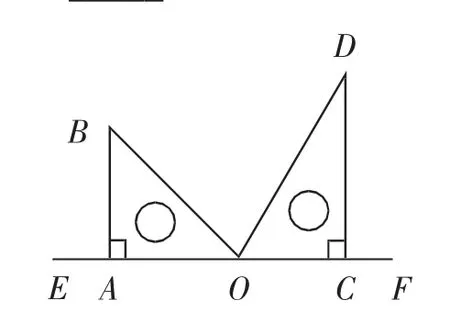
图1

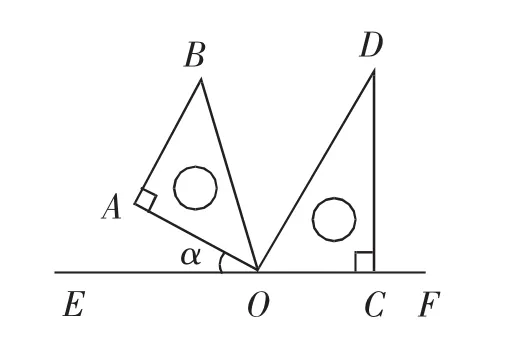
图2

诊断分析：第（1）问求∠BOD的度数，考查平角等于180°，也可以考查余角（过O作EF的垂线分割成两个直角），进行角的和差计算.第（2）问学生可以通过操作按照顺时针旋转的顺序依次发现，OB平分∠AOD，平分∠AOC，平分∠DOC时α的值.当OB平分∠AOD时，只需∠BOD=∠AOB，所以由第一问75°-α=45°，求得α=30°；当OB平分∠AOC时，只需∠BOC=∠AOB，即75°＋60°-α=45°，所以可得α=90°；当OB平分∠DOC时，α=75°＋30°=105°.第（3）问OA所在直线恰好平分∠COD时∠AOE的值恰好为互补的两个角，即从直线EF的上方转到了下方，进行完整的一周的旋转.但考虑到第（2）问学生也可以直接通过角度的加减得到答案，没有较好地考查一元一次方程知识的运用，且第（3）问还是考查角平分，没有多大必要，需要改进，所以有了二稿.

二稿：题干和第（1）（2）问保持不变只改变第（3）问.

（3）在（2）的条件下，是否存在∠BOC=2∠AOD？若存在求出此时α的值，若不存在，请说明理由.

诊断分析：本小题抓住了在旋转过程中，∠BOC和∠AOD的大小在发生变化，从而研究它们在变化过程中存在的两倍关系，在旋转的过程中还需要学生关注到一开始两角都在减小，但∠AOD转到AO与OD重合后又开始变大，所以要以OD为界即α在120°前后分段讨论.有较好的区分度，又考查了核心知识一元一次方程的应用，题目的层次感和区分度都较为理想.但在审稿时各县市的教研员提到一点，（2）（3）两小问都需要分类讨论，难度偏大，也考虑到2018年2月考试后就要过农历的新年，同时七年级的孩子应该多一些鼓励给孩子信心，快快乐乐过新年，建议降低难度.基于对孩子的人文关怀，笔者忍痛割爱有了第3稿，同时改进了一些语言上的表述，让试题更简洁、更严谨.

定稿：26.（8分）已知一副三角板按如图1方式拼接在一起，其中边OA、OC与直线EF重合，∠AOB=45°，∠COD=60°.

（1）求图1中∠BOD的度数.

（2）如图2，三角板COD固定不动，将三角板AOB绕着点O按顺时针旋方向转一个角度α，在转动过程中当两块三角板都在直线EF的上方时：

①若∠BOC为90°，求旋转角度α的值.

②是否存在∠BOC=2∠AOD？若存在，求此时的α的值；若不存在，请说明理由.

诊断分析：最后的定稿将第2稿的第（2）问角平分时的分类讨论删除，换成∠BOC为90°时，求旋转角度α的值，难度降低了不少，但整个试题围绕旋转角度α展开，环环相扣，试题有较好的层次感，第（2）问的第②小问若要解答完整还是有一定难度的，试题有一定的区分度，能较好地考查核心知识，考查学生的分类意识、方程思想等数学素养.

三、试题解答及分值

解：（1）∠BOD=75°.（2分）

（2）①当∠BOC=90°时，α=45°.（2分）②ⅰ当0≤α≤120°时，∠AOD=120°-α，∠BOC=135°-α.

当∠BOC=2∠AOD时，135°-α=2（120°-α），所以α=105°，成立.（2分）

ⅱ当120°＜α＜135°时，∠AOD=α-120°，∠BOC=135°-α.

当∠BOC=2∠AOD时，135°-α=2（α-120°），所以α=125°，成立.（2分）

所以当α=105°，α=125°时存在∠BOC=2∠AOD.

四、命题思考

1.考查核心知识，聚焦核心素养

本题命制选取学生最熟悉的三角板为题材，以《义务教育数学课程标准（2011年版）》为指导，要求学生能探索图形变换的性质，感悟图形研究中运动变换的思想，以动态和相互联系的观点理解图形的性质和相互关系，发现运动中的变与不变，研究变化中的数量关系.本题作为整份试卷的压轴题，重点考查了七年级在几何和代数上的两大核心知识，角的相关知识和一元一次方程的应用.本题可以通过操作去发现问题，从两块三角板的摆放、旋转通过数学抽象转化成数学模型，可以直观感受图形的变化，聚焦直观想象、数学抽象、数学建模，又通过等量关系列出一元一次方程，通过方程求解，考查学生的运算能力，可以说本道压轴题既考查七年级上册的核心知识，又充分聚焦了初中数学的几大核心素养.

2.突出数学思想，兼顾人文关怀

从试题的设计初衷到最后的敲定终稿，除了关注核心知识的考查，还尤为关注数学思想方法的考查，从初稿的角平分线的分类讨论，到定稿角二倍关系研究中的分类讨论，由“形”：图形的运动中的分界位置（本题中AO与DO重合时）前后变化，对应“数”（∠AOD由120°减小到0°，再变大的过程），都突出了数学思想方法的考查.另外定稿的降低难度，以及答案分值的设定，都充分体现对不同阶段学生的人文关怀，七、八、九三个年级可以逐步提高一点难度，这使得这份试卷既有深度又有温度，命制一份试卷真的要从多方面思考，不容易.

对于最后一题的解答，能解答完整的学生也不太多，30名学生的一个考场平均比例不到15%.统计结果显示嘉兴市海盐县整卷的平均分为77分，前15%学生的分数线在92分，较好地达成了预定目标.