基于前后向拟合的色谱重叠峰分峰方法

高文清，张俊良，王 艳，刘 蔓，Hu JunJack， 俞建成，Tang keqi

(1.宁波大学信息科学与工程学院，浙江 宁波 315211；2.中国人民解放军陆军总医院，北京 100700； 3.中国科学院宁波材料技术与工程研究所，浙江 宁波 315201)

色谱技术作为复杂组分分离和定量分析的手段之一，具有分析速度快、分离效率高、样品用量少等优势[1]。应用色谱技术分离复杂成分，在理想实验条件下，每个单峰对应一个组分，但实际上，当两个或多种成分含有相似的结构或性质时，很容易形成重叠峰，这将为后续的定性和定量分析带来困难[2]。因此，如何有效分离重叠色谱峰，是目前亟需解决的重要问题之一[3-4]。实际应用中，大多数重叠峰是双峰重叠，所以本工作只研究2个峰重叠的分离方法。

针对色谱重叠峰分离问题，主要的分离方法有基于几何的、基于代数的和基于模式识别的分峰方法[5]。其中，基于几何的分峰方法主要有垂线法和切线法，计算速度快、直观，适用于实时在线分析，已被商业集成所应用，但其分离精度会随着色谱峰重叠程度的增加而降低，在严重重叠的情况下，这两种方法的定量误差都很大[6]。针对这一问题，叶国阳等[7]提出了交点垂线法和比例分配法，使定量精度得到了大幅提高，但该方法依赖于重叠峰的两个极大值点，而且在只有一个极大值点，即肩峰的情况下，还需要通过做重叠峰拐点切线，求切线交点的方法求得另一个极大值点。另外，拖尾峰和前延峰在实际应用中也很常见，该研究并未探讨这两种峰的适用度。严彩娟[8]基于重叠峰相似性原理提出了纵向迭代法，该方法从远离重叠区域的前后沿开始拟合，对色谱峰重叠区域进行修正，并研究了拖尾重叠峰、前延重叠峰，但该方法要求重叠峰具有谷点。基于代数的分峰方法主要有基于高斯函数的谱峰拟合算法[9]、基于最小二乘法的谱峰拟合算法[10]、小波变换算法[11]等。这些算法能够得到较好的计算结果和分峰效果，然而在分峰过程中，它们需要一定的参数估计与优化、模型选择等步骤，计算量大，消耗时间长，不适用于实时在线处理[12]。基于模式识别的分峰方法中，免疫算法分离效果较好，但它仅适用于已知成分的重叠峰分离，应用受限[13]。

1 前后向拟合分离重叠峰理论

1.1 重叠峰数学模型

色谱分离过程中，由于性质或结构上的微小差异，各组分与流动相和固定相的相对运动产生的作用力以及两相的分配系数不同，使得各组分在色谱柱上的保留时间不同，当两种物质具有相似的性质或结构时，从色谱柱流出的时间非常接近，产生重叠峰[7]。根据重叠峰产生的原理，假设重叠峰的单组分峰具有相似性，具体特征如下：1) 所有单峰的峰形相似；2) 单峰之间可以通过一个系数相互转换；3) 每个单峰的半峰宽相同。

为了便于理解，构建了重叠峰的数学模型，示于图1，其方程如下：

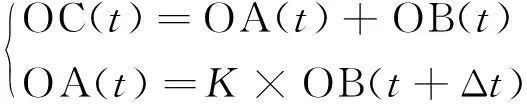
(1)

式中：OC代表重叠色谱峰；OA、OB分别代表构成重叠峰的两个单峰；+代表两个单峰相加；×代表两个单峰之间的尺度变换；K代表尺度变换因子，即两个单峰的峰高比；Δt为平移跨度(Δt>0)。

1.2 前后向拟合算法

从图1可以看出，单峰OA的前沿、单峰OB的后沿分别与重叠峰OC的前沿、后沿相差很小，即它们受到重叠的影响很小，因此，本工作从此处着手对重叠峰进行分离。以tM、tN、tS、tT分别代表M、N、S、T四个点的时间坐标，hM、hN、hS、hT分别代表其在相应时间上的峰强。

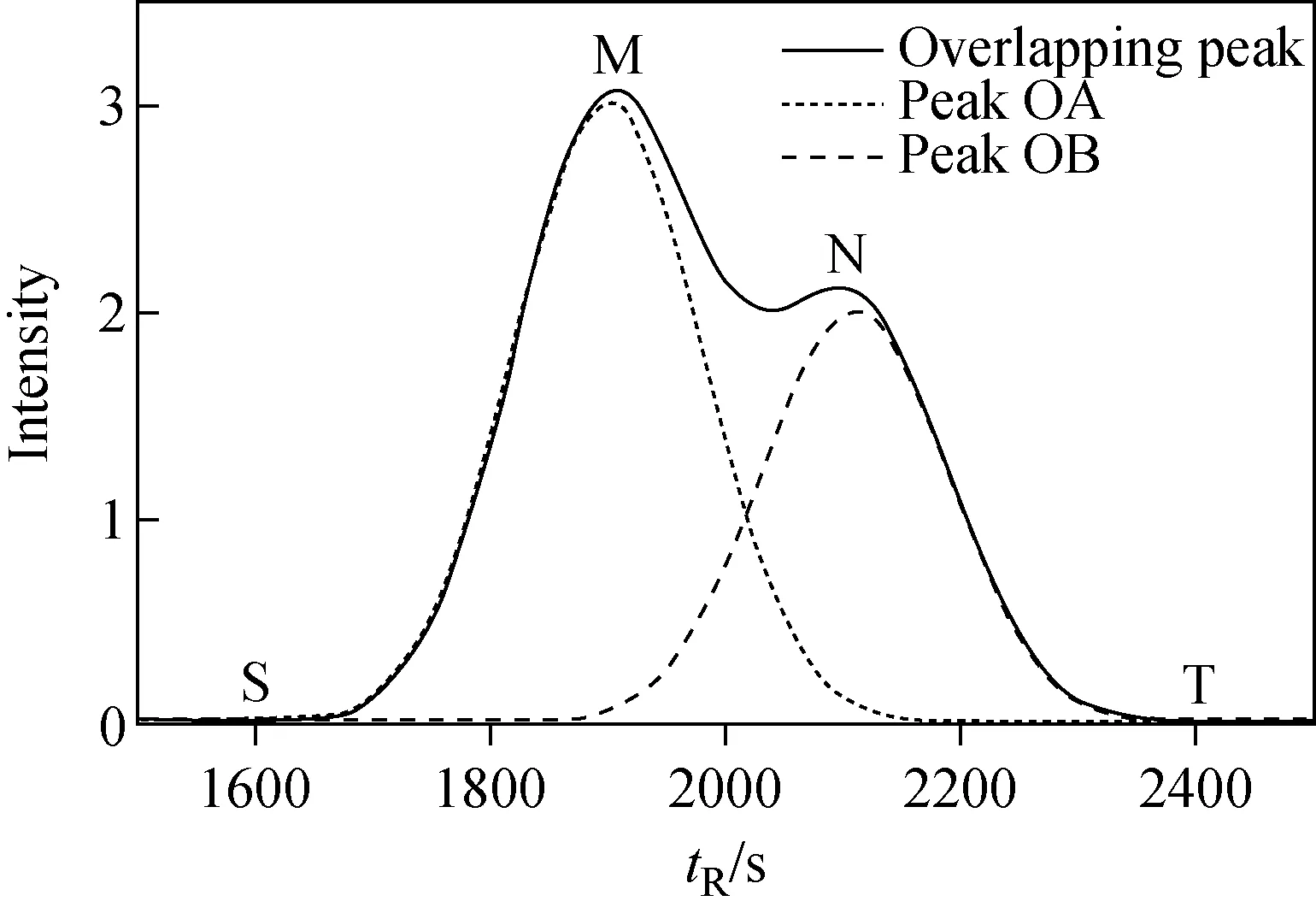
注：M、N分别是重叠峰的两个极大值点； S、T分别是后向拟合、前向拟合的起始点 图1 重叠峰的数学模型Fig.1 Mathematical model of overlapping peaks

前后向拟合算法主要分为前向拟合和后向拟合两步。

定义S、T分别为后向拟合和前向拟合的起始点，对于第一次前向拟合和后向拟合，具体步骤如下：

泄露500 d后，上覆第四系松散孔隙含水层进一步向南侧迁移，污染羽状物扩散范围有逐渐增加，而下伏岩溶含水层仍然未见受到明显污染，未出现明显污染羽状物聚集及渗漏。

1) 从T点出发开始前向拟合。将重叠峰的极大值M点当作单峰OA暂时的极大值点(以m点表示)，T点当作单峰OB暂时的极大值点(以t点表示)，以此修正单峰OB的峰高点。此时峰高比可以定义为：

kft=hm/ht

(2)

2) 定义τ(τ>0)为时间跨度，其大小可以根据需求调节。沿着时间轴将t点向重叠区域推进τ，现在时间表示为tt-τ。

3) 根据式(1)，拟合单峰OB在时间tt-τ到tt部分的峰形，把拟合出来的峰对应于tt-τ点记作t1。此过程可由式(3)表示：

(3)

式中，OBft1(t)为前向拟合第一次迭代之后得到的单峰OB的后沿，此时OBft1(t)暂时的峰高点被记作ht1，同时峰高比可以表示为：

kft1=hm/ht1

(4)

4) 依此类推，前向拟合经过第(n+1)(n=0,1…)次迭代之后，tt-(n+1)τ到tt之间的峰形可以表示为：

(5)

kftn+1=hm/htn+1

(6)

5) 比较前向拟合过程前后两次迭代得到的htn与htn+1值。如果htn≥htn+1，并且两者之间的差值处于设定的范围内，就完成了第一次前向拟合，可得到单峰OB暂时的后沿OBftn(t)和极大值htn。

6) 结束第一次前向拟合后，从S点开始类似的后向拟合过程。将S点当作单峰OA暂时的极大值点(以s点表示)，保持单峰OB暂时的极大值htn不变，重复上述5个步骤，可以得到ts到ts+(n+1)τ之间的峰形，记作OAbsn+1(t)：

(7)

kbsn+1=htn/hsn+1

(8)

如果hsn≥hsn+1，而且它们的差值落在一定的范围内，第一次后向拟合过程即停止。此时，可得到单峰OA暂时的前沿OAbsn(t)和极大值hsn。

第一次前向拟合和第一次后向拟合的结果示于图2。

经过第一次完整的前后向拟合过程后，根据上述6个步骤，进行第R(R=2,3,…)次前后向拟合。此时，可以得到单峰OA新的前沿OAbRsn和极大值hRsn，单峰OB新的后沿OBfRtn和极大值点hRtn。最后，通过色谱重叠峰相似性原理，单峰OA新的后沿OAback可以由单峰OB新的后沿OBfRtn得到，单峰OB新的前沿OBfront可以由单峰OA新的前沿OAbRsn得到。因此，完整的单峰可以表示为：

OA(t)=OAbRsn(t)+OAback(t)

OAback(t)=(hRsn/hRtn)×OBfRtn(t-ttn+tsn)

(9)

OB(t)=OBfRtn(t)+OBfront(t)

OBfront(t)=(hRtn/hRsn)×OAbRsn(t+ttn-tsn)

(10)

为了更好地理解该算法，将经过3次前后向拟合得到的分峰效果图示于图3。

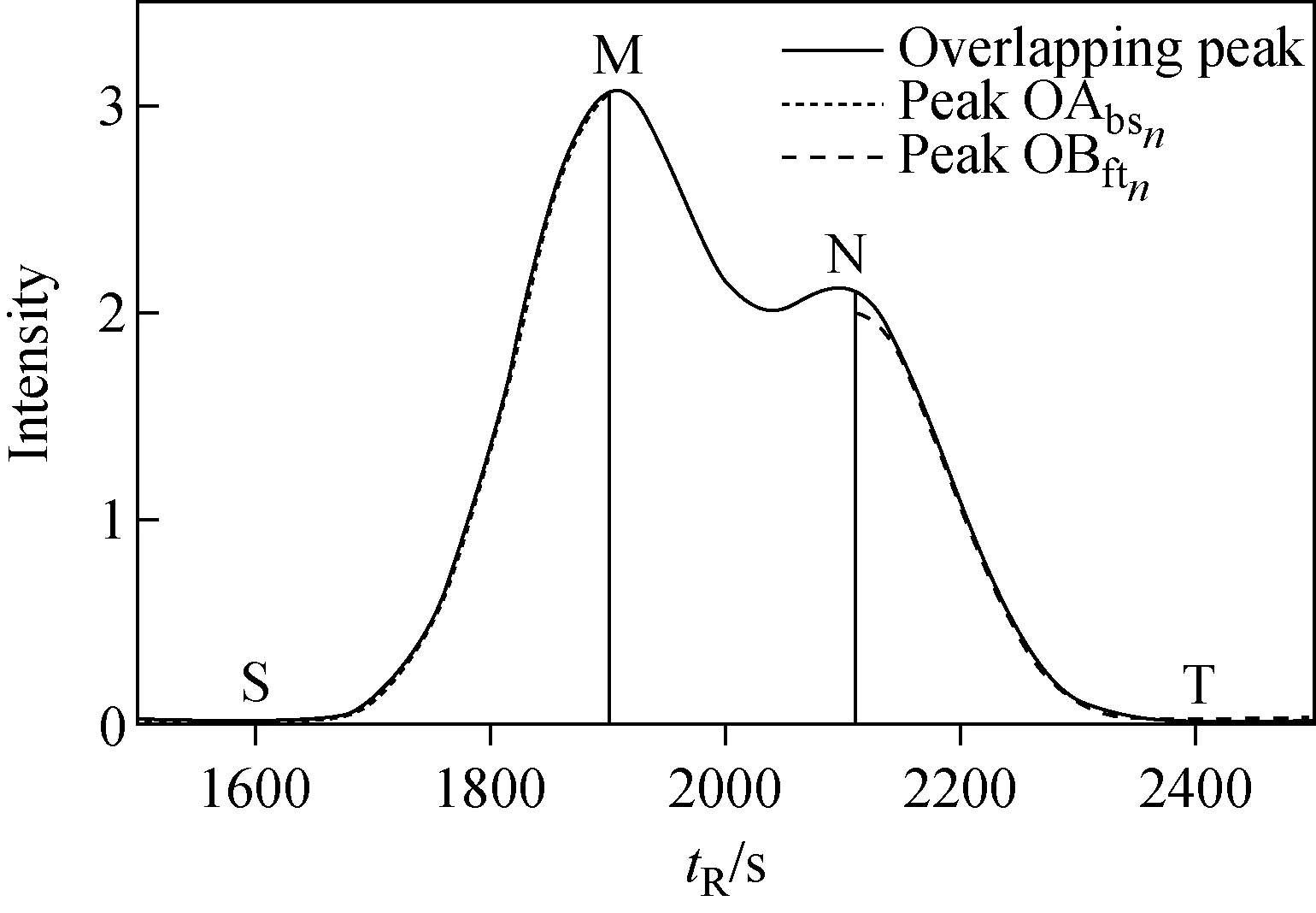
图2 第一次前向拟合得到的单峰OB的 后沿OBftn和第一次后向拟合得到的 单峰OA的前沿OAbsnFig.2 Back edge OBftn of single peak OB obtained from the first forward fitting and the front edge OAbsn of single peak OA obtained from the first backward fitting

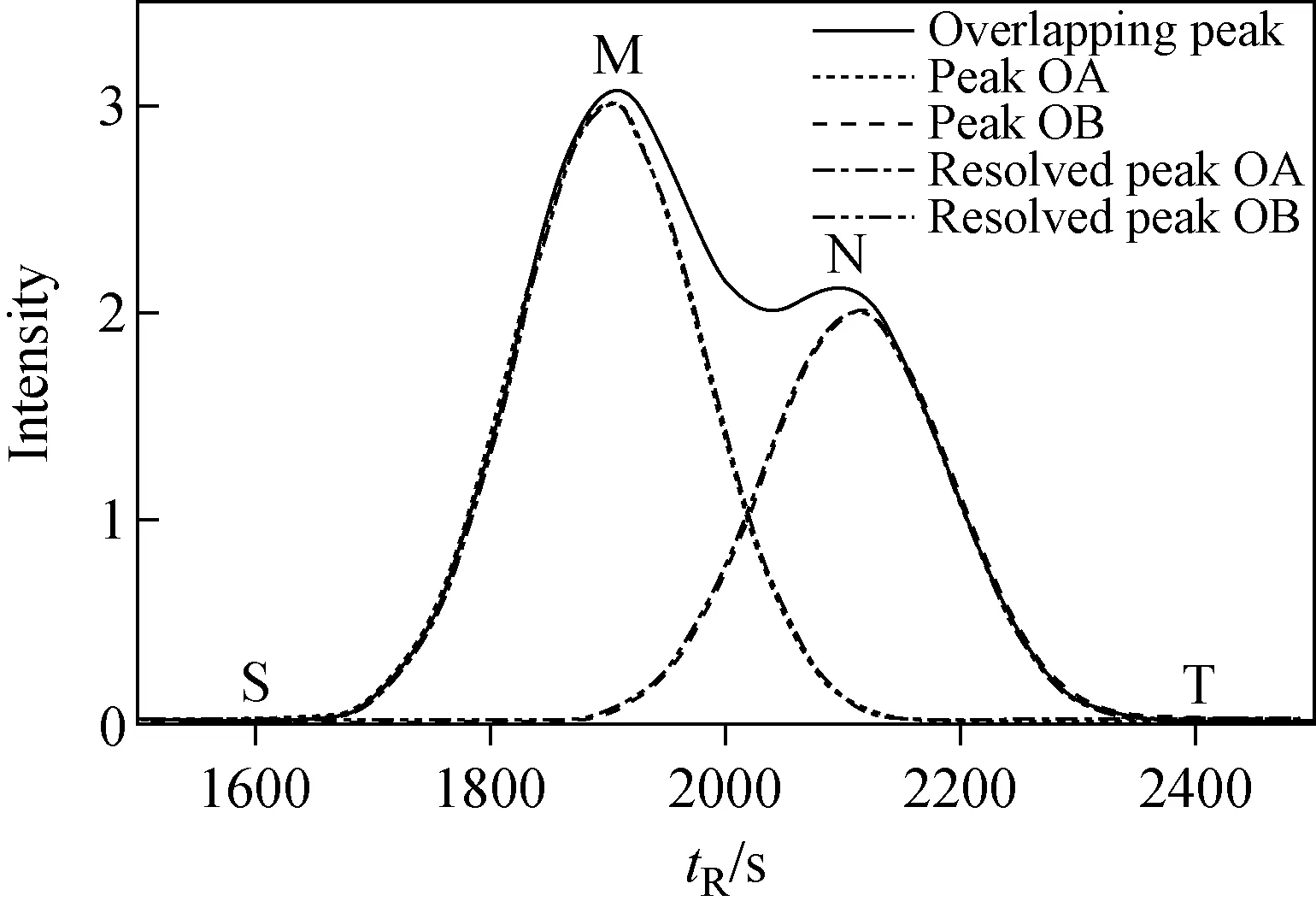
图3 经过3次完整的前后向拟合得到的 重叠峰分峰效果图Fig.3 Resolution result of overlapping peaks after three complete forward and backward fittings

2 实验部分

2.1 仪器及试剂

GC-MS 7890B-5977A气相色谱-质谱联用仪：美国Agilent公司产品；间二甲苯甲醇溶液、对二甲苯甲醇溶液(1 000 mg/L)：北京坛墨质检科技有限公司产品；实验数据：使用Matlab R2014a编写的程序进行计算。

2.2 实验条件

2.2.1色谱条件 色谱柱：DB-WAX柱(30 m×0.25 mm×0.25 μm)；升温程序：80 ℃保持4 min，以20 ℃/min升至200 ℃，保持1 min；载气(He)流速1 mL/min；进样量0.5 μL；分流比20∶1。

2.2.2质谱条件 电子轰击(EI)离子源；电子能量70 eV；传输线温度240 ℃；离子源温度230 ℃；溶剂延迟2 min。

2.3 仿真实验设计

根据塔板理论，指数修正高斯(EMG)模型可以很好地描述色谱流出曲线，因此，本工作采用EMG模型来构造色谱峰[14]。影响色谱重叠峰峰形的3个主要因素为分离度、两个单峰的峰高比、拖尾因子。分别针对这3个影响因素对重叠峰峰形进行划分，然后对比垂线法、交点垂线法、比例分配法和前后向拟合法在不同影响因素情况下的分离性能。

1) 有谷点重叠峰：设定分离度为0.797，峰高比分别为1∶4、2∶3、1∶1、 3∶2、4∶1。

2) 无谷点重叠峰，即肩峰：设定峰高比分别为4∶1和1∶4，分离度分别为0.478、0.345。

3) 前延重叠峰和拖尾重叠峰：设定峰高比为4∶1，分离度为0.797，拖尾因子分别为0.766 2、0.853 8、0.975 1、1.031 6、1.172 5、1.417 2。

以上实验设计中，常见重叠峰类型及重叠程度高低均包含在内，选取的参数比较具有代表性。

2.4 真实实验设计

为了更好地验证前后向拟合算法的可行性，选择对二甲苯和间二甲苯进行分离实验[12]。配制一系列不同浓度比的间二甲苯和对二甲苯的混合甲醇溶液，具体情况列于表1。为了评估算法的有效性，同时分别配制了一系列与各混合溶液中浓度相同的对二甲苯、间二甲苯标准溶液，以获取两者的单峰。

3 结果与讨论

通常情况下，峰面积是定量分析的一种衡量标准，因此，本工作通过计算真实峰面积与垂线法、交点垂线法、比例分配法、前后向拟合法所得到的单峰面积之间的误差，评估各个方法的性能。误差可由式(11)计算：

(11)

式中，Amethod是由垂线法、交点垂线法、比例分配法、前后向拟合法计算得到的单峰面积；AR是构成重叠峰的每个单峰的面积。

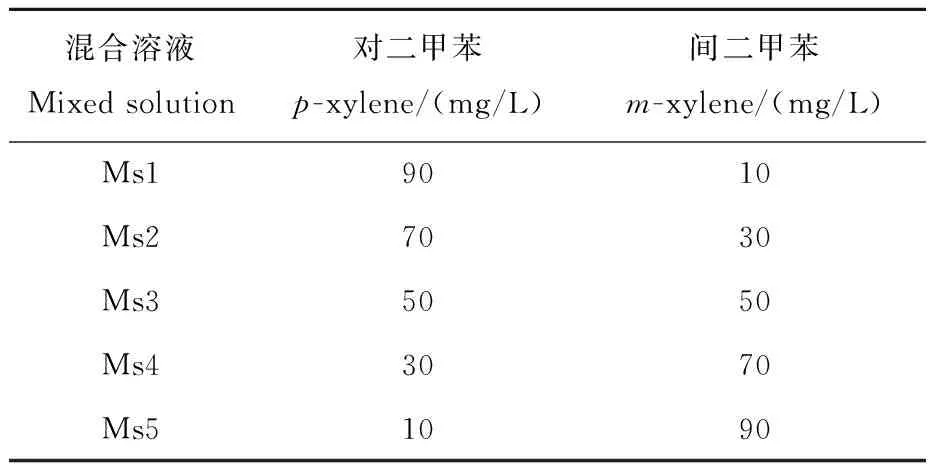
表1 对二甲苯和间二甲苯混合溶液配比Table 1 Mixture ratios of p-xylene and m-xylene

3.1 仿真结果分析

有谷点重叠峰和无谷点重叠峰的计算误差列于表2。从表2可以看出：对于有谷点重叠峰(No.1～5)，分离误差会随着峰高比的增大而增大，垂线法的分离误差最大，交点垂线法和比例分配法次之，而前后向拟合方法的误差处于±0.01%范围内；对于无谷点重叠峰(No.6～9)，垂线法是无法使用的，通过做重叠峰拐点处的切线交点求得重叠峰的两个极大值点后，使用交点垂线法和比例分配法进行分峰，得到的最高误差分别可达18.93%和26.24%，但使用前后向拟合方法进行计算，其最大误差仅为0.51%；从No.1、No.8、No.9和No.5、No.6、No.7这两组数据来看，在同一峰高比的情况下，随着分离度的降低，重叠峰的重叠程度增大，垂线法、交点垂线法、比例分配法的分离误差变化幅度较大，而前后向拟合方法的分峰误差则相对平稳地处于较小范围之内。同时，对于No.7无谷点重叠峰，虽然其分离度很小，但前后向拟合方法的分峰轮廓与真实单峰几乎重合，实验效果图示于图4。

在实际色谱分离实验中，由于进样量大、色谱柱污染等原因，可能导致色谱峰拖尾，因此，本实验对4种方法分离拖尾峰的性能进行了研究，结果列于表3。在同一峰高比和分离度的情况下，随着重叠峰拖尾程度的增加，4种方法的分离误差均有随之增大的趋势，与表2中No.5无拖尾实验数据相比，这种现象也得到了验证。随着拖尾程度的增大，前后向拟合方法的分峰误差明显小于其他三种方法，整体误差稳定在±0.11%以内。前后向拟合方法分离No.10重叠峰实验效果图示于图5。由图5可见，对于存在严重拖尾的重叠峰，前后向拟合方法不仅可以将误差控制在较小范围内，其轮廓也与真实单峰较一致。

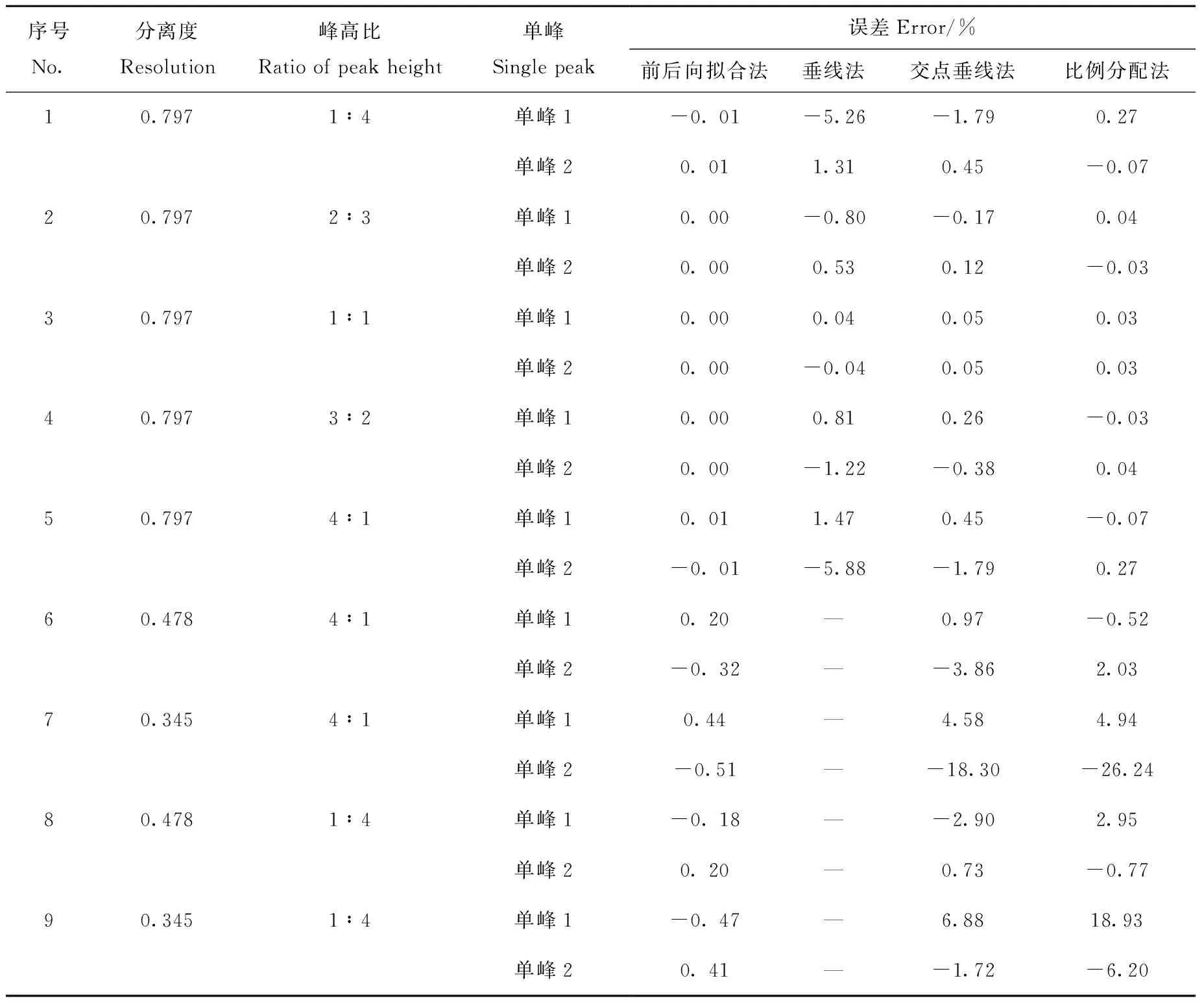
表2 有谷点重叠峰(分离度为0.797)和无谷点重叠峰(峰高比分别为4∶1、1∶4)的计算误差Table 2 Resolution results of overlapping peaks with valley point under resolution of 0.797 and those of overlapping paks without valley point under peak height ratios 4∶1 and 1∶4, respectively

3.2 真实结果分析

为了进一步验证前后向拟合方法的性能，使用气相色谱-质谱联用仪开展了一组对二间苯和间二甲苯同分异构体的重叠峰分离实验，并分别采用4种方法对重叠峰进行分离，结果列于表4。

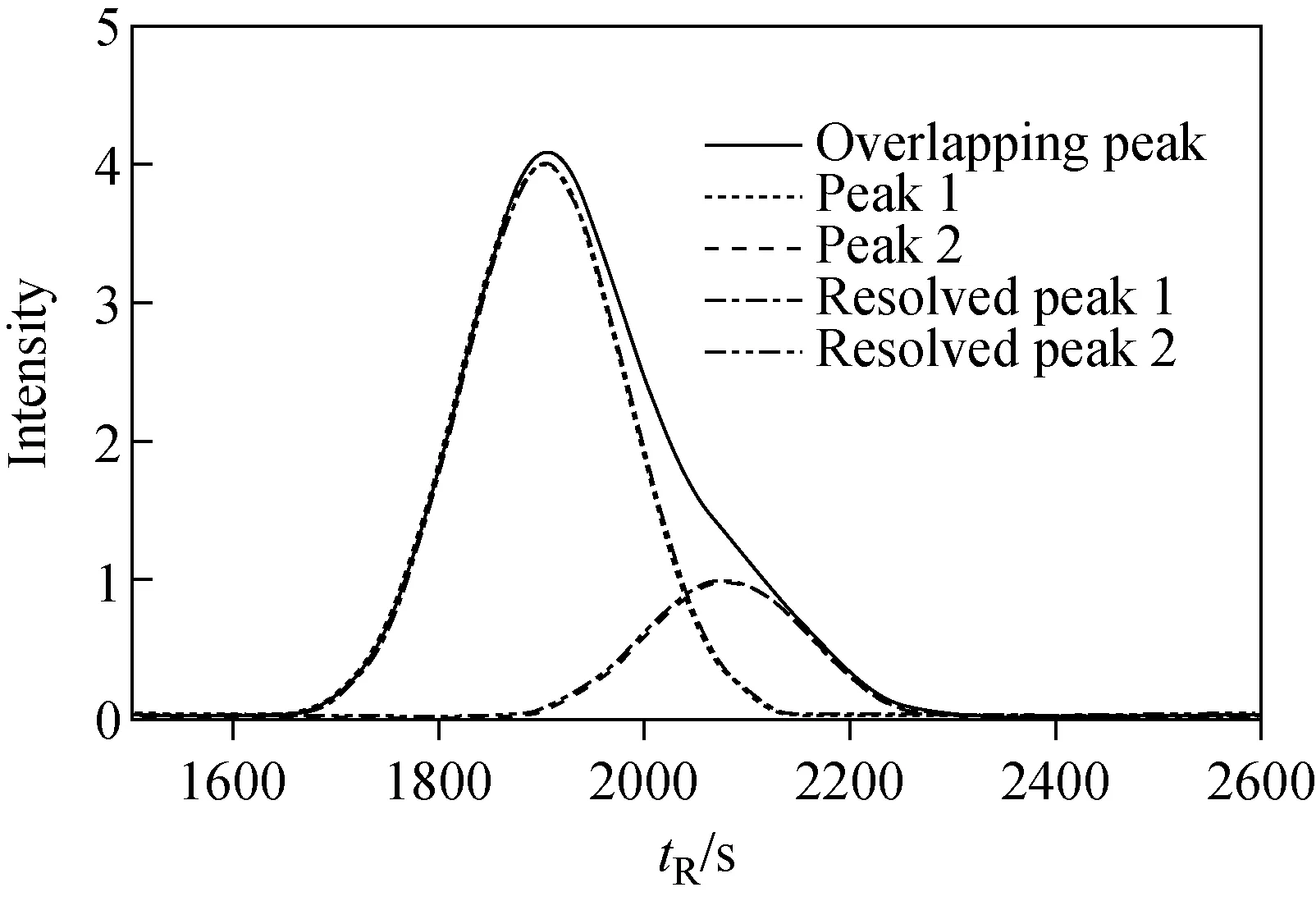
图4 前后向拟合方法分离No.7重叠峰

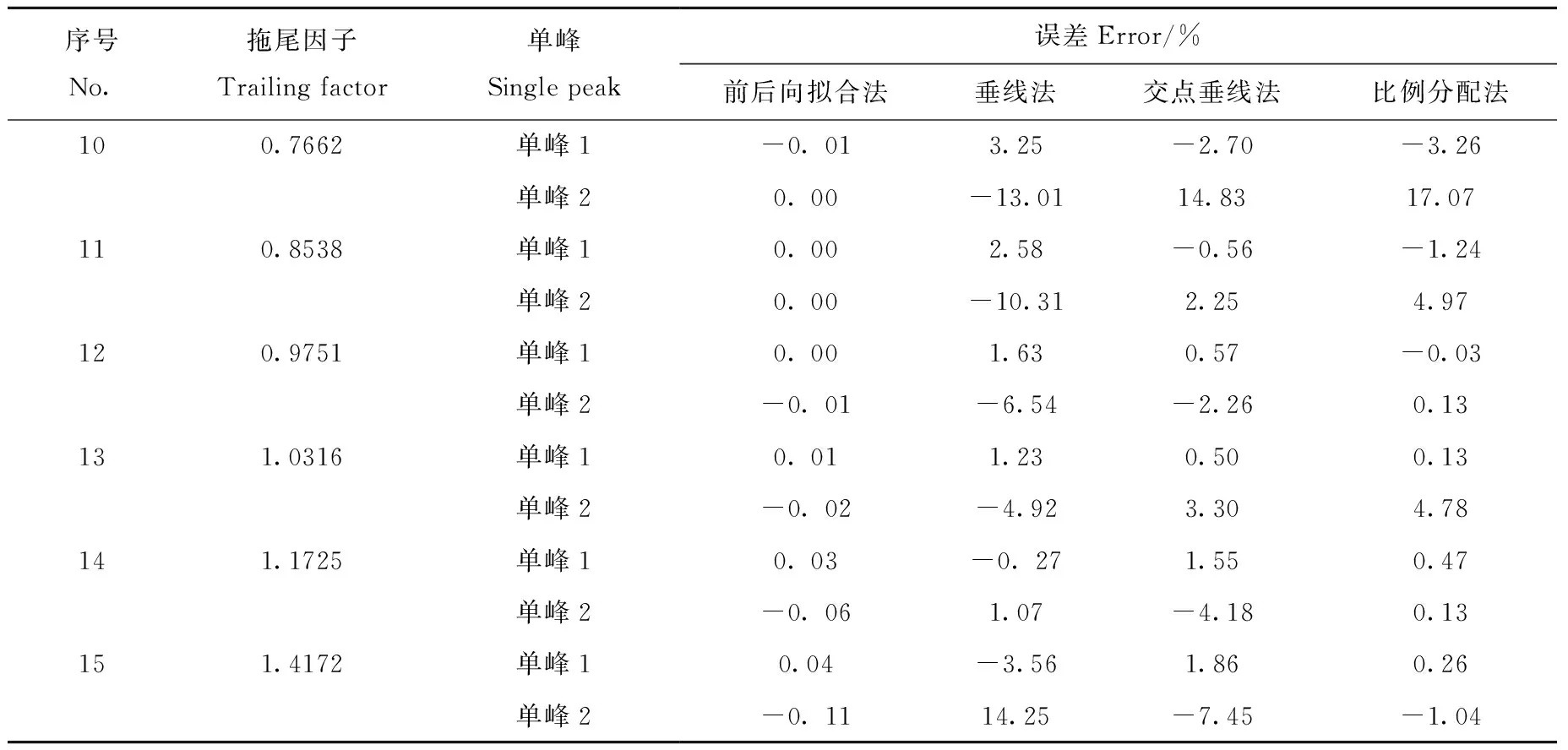
序号No.拖尾因子Trailing factor单峰Single peak误差Error/%前后向拟合法垂线法交点垂线法比例分配法100.7662单峰1-0. 013.25-2.70-3.26单峰20. 00-13.0114.8317.07110.8538单峰10. 002.58-0.56-1.24单峰20. 00-10.312.254.97120.9751单峰10. 001.630.57-0.03单峰2-0. 01-6.54-2.260.13131.0316单峰10. 011.230.500.13单峰2-0. 02-4.923.304.78141.1725单峰10. 03-0. 271.550.47单峰2-0. 061.07-4.180.13151.4172单峰10.04-3.561.860.26单峰2-0. 1114.25-7.45-1.04

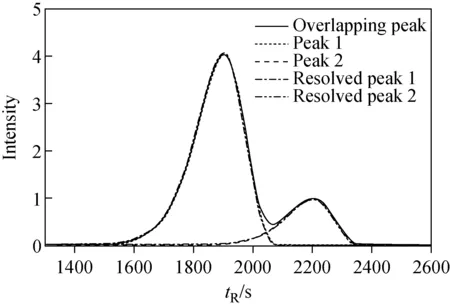
图5 前后向拟合方法分离No.10重叠峰实验效果图Fig.5 Resolved profiles of No.10 leading overlapping peak by forward-backward fitting method

从表4可以看出，对于Ms3溶液，垂线法的分离误差比前后向拟合法的误差小，这是因为垂线法更适用于分离两个含量相同的单组分，此时两个单峰受到重叠影响的程度相似，因此垂线法的分峰误差最小，但前后向拟合法仍能将Ms3溶液的分离效果控制在0.8%以内。对于其他4种比例的混合溶液，前后向拟合方法的整体误差均小于其他3种方法。随着两种成分比例的增加，其他3种方法的分离误差变化较大，而前后向拟合方法的误差变化则比较平稳。前后向拟合方法分离Ms1重叠峰的结果示于图6。

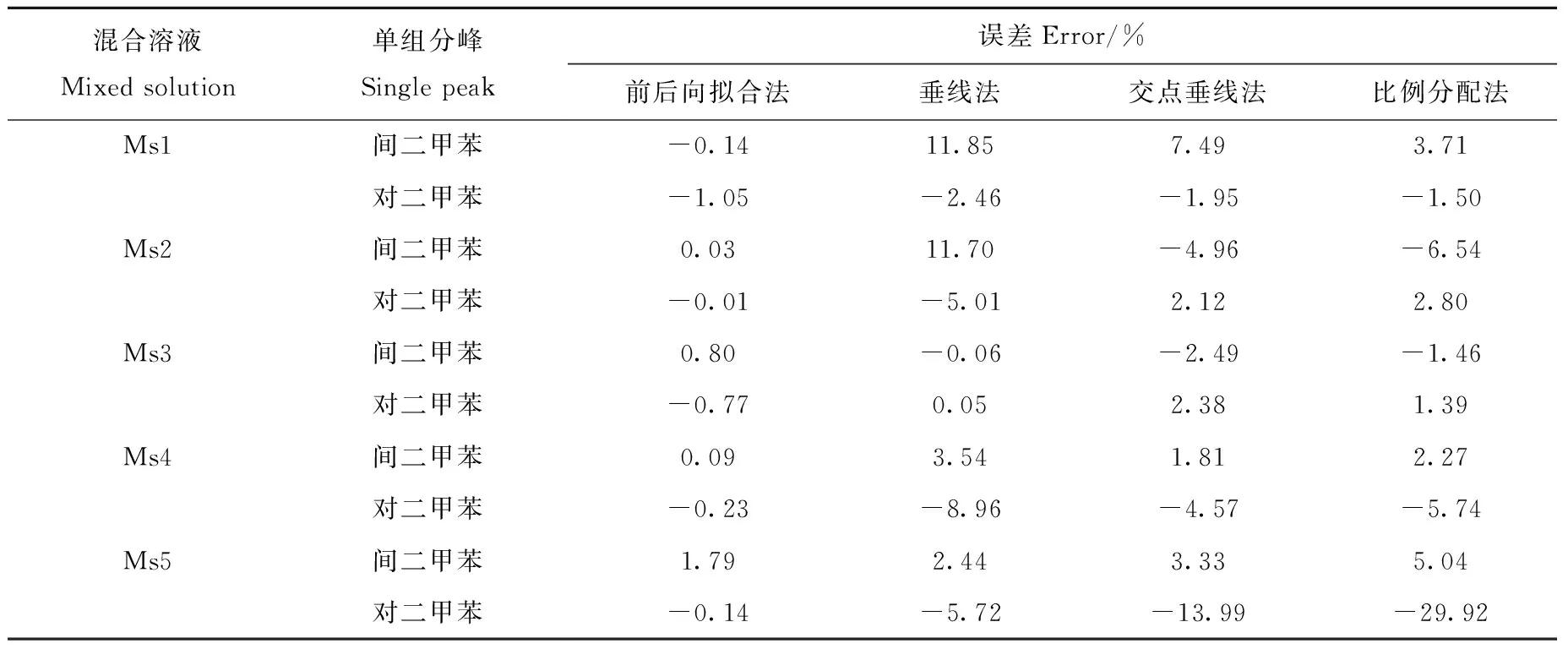
表4 对二甲苯和间二甲苯的重叠峰分离结果Table 4 Resolution results of overlapping peaks of p-xylene and m-xylene

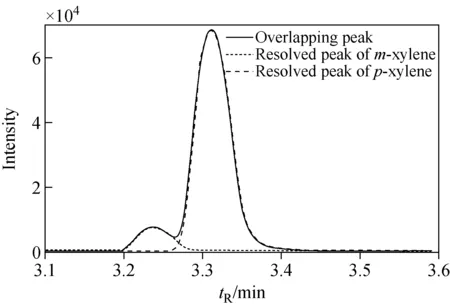
图6 前后向拟合方法分离Ms1重叠峰效果图Fig.6 Resolved profiles of Ms1 overlapping peak by forward-backward fitting method

4 结论

根据重叠峰相似性原理，提出了前后向拟合分峰方法，通过仿真实验和真实实验，与垂线法、交点垂线法、比例分配法的分离精度进行对比。结果表明，前后向拟合方法的分离误差可稳定在1.8%以内，分离精度高于常规的3种分离方法，而且无需依赖两个极大值点，且能适应多种常见的重叠峰类型，即使对于重叠程度较高或具有拖尾的重叠峰，前后向拟合方法也具有较好的分峰效果。