多速率信号处理系统设计与实现

谢海霞，孙志雄

（海南热带海洋学院海洋信息工程学院，海南三亚572022）

软件无线电系统中各个模块的信号速率是不同的，它实质上通过抽取和内插的方法来改变数字信号的速率，多速率信号处理是数字上变频、下变频技术处理的依据。实际应用中，通常采用CIC滤波器，HB滤波器，多相结构滤波器和FIR滤波器等改变信号速率且避免频域混叠[1-3]。

文中对不同级数、不同抽取因子的CIC、HB作性能对比，提出一种抽取滤波器级联组的设计方案，旨在解决在AD采样速率很高，所需基带信号的带宽很窄，且计算量减少时等问题，从而找出最适用的多速率滤波器，最后通过MATLAB仿真实现[4-6]。

1 多速率信号处理

多速率信号处理技术的基础理论是抽取和内插，如D倍抽取是每隔D-1个采样点抽取一个点即去掉多余数据降低采样率的过程，I倍内插是相邻抽样点之间插入I-1个零值点即增加数据提高采样率的过程。从时域上直接进行抽取和内插会产生频域的扩展和压缩，导致频谱失真。实质上多速率信号处理是先通过时域上的抽取和内插，再结合滤波器一起操作，以达到转换信号速率，保证有用频带内没有频谱混叠的目的。当A/D采样速率很高，所需基带信号的带宽很窄时，那么抽取因子D必然会很大，如采用一级抽取滤波器完成，则该滤波器阶数非常高，计算量大，难实现。实际实现中常采用多级级联抽取结构来实现，同时减少计算量。经典多速率信号抽取处理结构如图1所示[7-9]。

图1 多速率信号抽取器结构图

1.1 积分梳状（CIC）抽取滤波器

在多级级联抽取器中，第一级一般采用积分梳状（CIC）抽取滤波器实现，因为其实现结构简单，适合高采样速率的情况。CIC滤波器系统传递函数为：

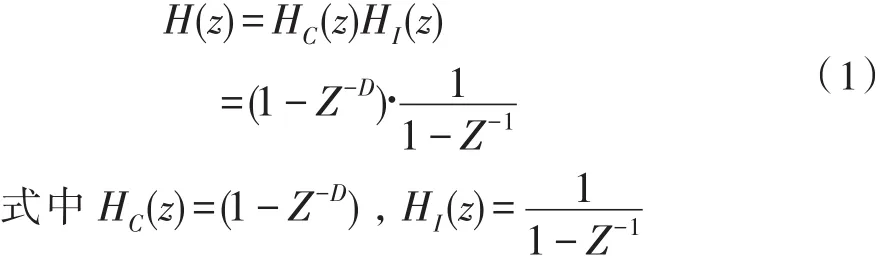
CIC滤波器由梳状部分和积分部分组成，其HC（z）是梳状滤波器，HI（z）是积分器，D为抽取倍数。其幅频响应为：

在[0，2π/D]频率区称为CIC滤波器的主瓣，其他区间为旁瓣。由于单级CIC滤波器的第一旁瓣电平比较大，只比主瓣电平低13.46dB，这意味着阻带衰减较差，难以满足实际使用要求。为了降低旁瓣电平，工程上多采用CIC多级级联的方法来解决[10-12]。

多级CIC抽取滤波器传递函数为：

N不宜取太大，一般取N=5时，阻带衰减达到67.3 dB，基本能满足实际要求。

1.2 补偿滤波器

多级级联CIC滤波器在降低了旁瓣电平，增大了阻带衰减的同时也大大提高了通带的失真。为了解决传统的CIC滤波器的通带波纹大、过渡带长、阻带衰减小，最直接最简单的办法就是在CIC滤波器之后级联一个补偿滤波器，它可以在一定程度上改善CIC滤波器的性能。

1.3 HB抽取滤波器

半带（HB）滤波器的阻带宽度（π-WA）与通带宽度（WC）是相等的，且通阻带波纹也相等，如图2所示[10-12]。

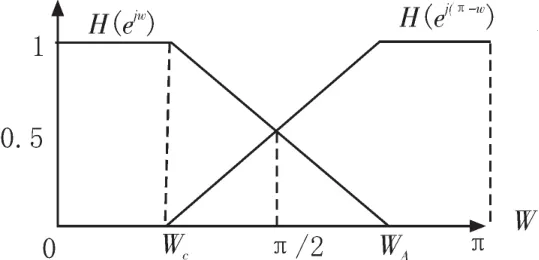
图2 HB滤波器频响图

半带滤波器的冲激响应h（n）除零点不为零处，在其余偶数点全都为零，所以采用半带滤波器来实现速率变换时，只需一半的计算量，适合处理较高速的数据。

1.4 FIR滤波器

FIR滤波器也是有限冲激响应滤波器，实现时是一个无反馈的电路。输出值均不受之前的输出状态影响，只与此时的与之前的输入有关。前面的CIC滤波器和HB滤波器是具有独特性质的FIR滤波器，而这里指的是普通型的FIR滤波器。值得注意的是如果将CIC滤波器或HB滤波器作为多级滤波器的最后一级时，过渡带往往过大且有混叠而不能满足滤波器特性的总体要求，所以后级必须要用其他类型的FIR滤波器对整体滤波器的输出进行整波滤除多余的频率分量。

1.5 多相滤波

多速率系统中只有抽取和内插实现速率转换，计算量很大。如果抽取滤波器的H（z）长度为N，抽取因子为D倍。则

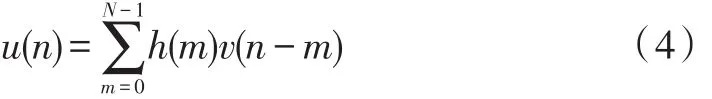
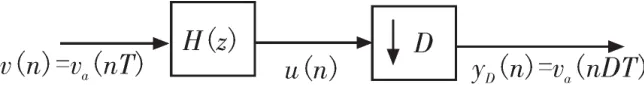
图3 D倍抽取器的示意图

对u（n）每D个点进行抽取一次输出，也就是只需在n=kD（k=1，2，…）时计算输出结果，计算复杂度为原来的1/D。为适用于实时系统，采取优化实现结构，提高计算效率，使用多相分解[13]。

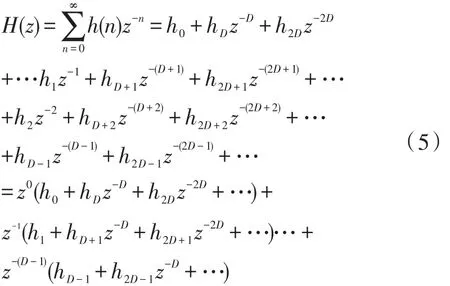
由式子（5）可得：

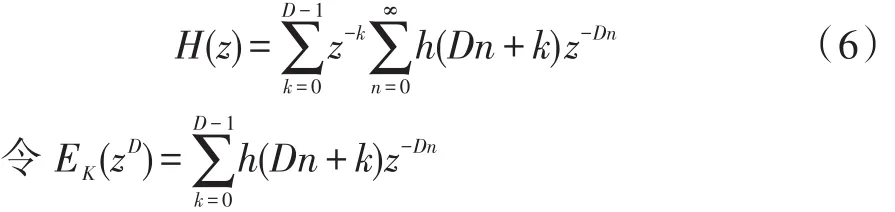
图4 多相滤波器结构图

根据多相滤波的原理，对整个多速率系统的非递归各个单元作多相并行处理，图4中滤波器EK(zD)为多相滤波器放在抽取之后进行，这就大大降低了对处理速度的要求，提高了实时处理能力。另一个好处就是每一分支路滤波器的系数由原先的N个减少为N/D个，可以减小滤波运算累积误差，提高计算精度[14-15]。

2 多速率信号抽取器的设计与实现

2.1 整个抽取器的性能指标

输入采样频率512 kHz，输出信号频率4 kHz，通带截止频率1.2 kHz，带内波动小于0.01 dB，阻带起始频率2 kHz，带外抑制大于65 dB。

2.2 抽取器的设计方案

设计的数字抽取器要求实现128倍的抽取，如采用单个滤波器实现时，需要2294阶，这样高阶数的滤波器实现起来非常困难。而解决这个难题的方法是采用滤波器多级级联来实现。通常用来实现抽取的滤波器主要有CIC抽取滤波器，HB抽取滤波器。本文对于抽取倍数D=128，取三级抽取倍数分别为 D1=32，D2=2，D3=2（D=D1D2D3），CIC滤波器能实现抽取倍数比较大的抽取，因此作为整个数字抽取滤的第一级，为了补偿CIC抽取滤波器的通带衰减速，在其后面级联一个补偿滤波器，而HB抽取滤波器能实现两倍抽取，所以D2和D3倍的抽取由HB滤波器来实现。FIR滤波器放在最后级联以进行较为精确的滤波整形，滤掉无用信号。

2.3 抽取器的设计

32倍抽取采用CIC抽取滤波器实现，阶数为3，其幅频响应如5图所示。

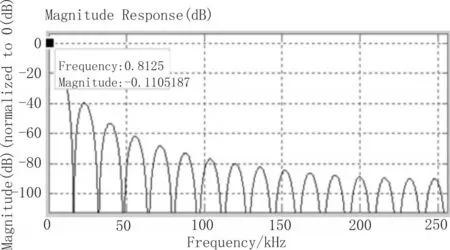
图5 CIC滤波器幅频响应图

从图5中可以看出，3阶32倍CIC抽取滤波器的通带内衰减较大，δ≈0.1102dB，显然不满足要求，所以后级必须对其进行通带补偿。

4倍抽取分别由两级2倍BH抽取滤波器来实现，经过32倍CIC抽取滤波器处理后，采样率下降至16 kHz，因此第一级HB滤波器的采样频率为16 kHz，利用MATLAB中的FDATool工具进行设计，输入设计参数，采用等波纹设计法（equiripple），可得到第一级HB滤波器的系数，如表1所示。第二级HB抽取滤波器的采样率为8 kHz，设计方法同第一级HB抽取滤波器，得到第二级HB滤波器的系数，如表1所示[16]。

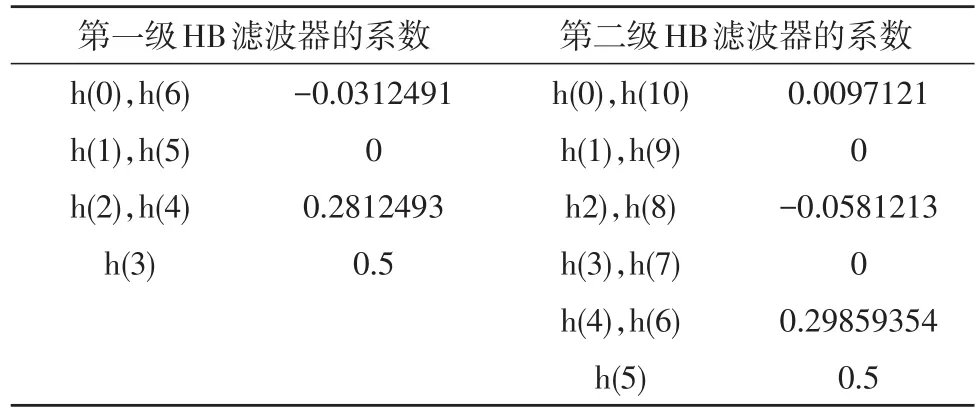
表1 两级HB滤波器的系数

补偿滤波器是实现CIC滤波器通带频率响应的修正。MATLAB带有的inverse sinc滤波器幅频响应与CIC滤波器的相反，因此可以用它来逼近。利用MATLAB中的filter builder工具设计该滤波器，其幅频响应如图6所示，在通带0.8 kHz边缘处幅度增加约0.11 dB，可以补偿CIC抽取滤波器的通带衰减。补偿滤波器的系数如表2所示。

最后一级FIR滤波器实现滤波整形。确定滤波器采样频率为8 kHz，通带截止为0.8 kHz，阻带起始频率为1.2 kHz，通带衰减0.01 dB，阻带衰减65 dB，采用FDATool设计可以得到所需的FIR滤波器的系数。其系数见表2。

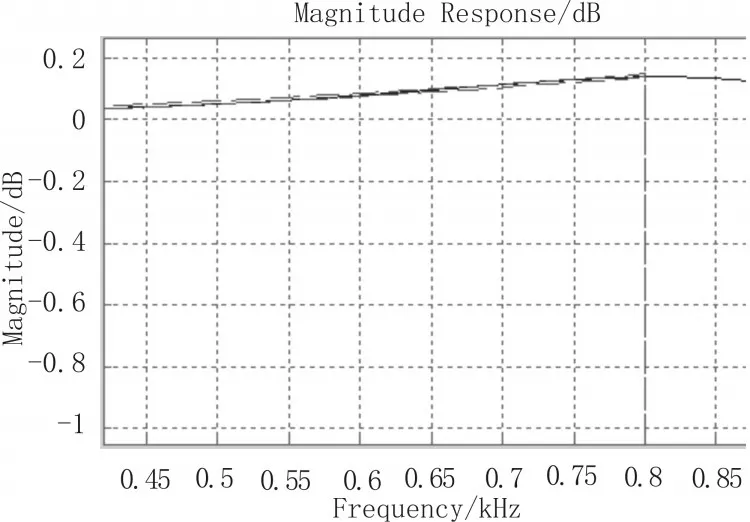
图6 补偿滤波器幅频响应图

将整个系统按照图1全部级联，各级滤波器及整体系统的幅频响应如图7所示，通过观察可以看出经过补偿滤波器以后整体的通带衰减改善了不少，幅频曲线十分平坦，整体的通带波动在0.01 dB以内，达到了的要求。

表2 补偿及FIR滤波器的系数

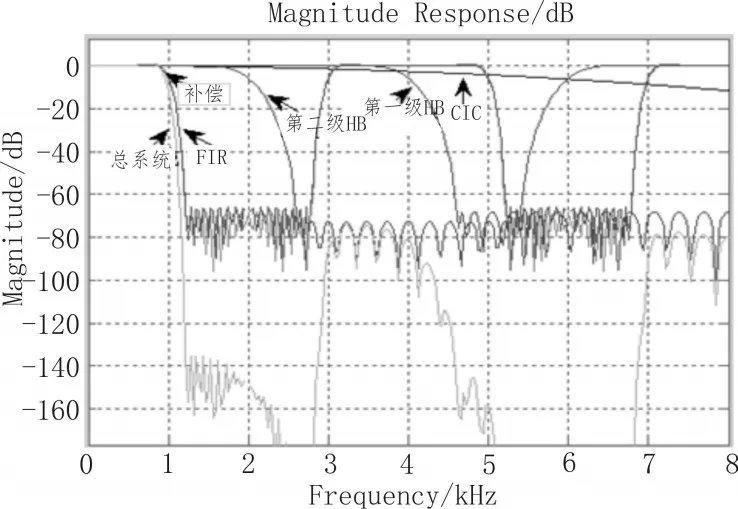
图7 各级滤波器及整体抽取器频谱图

2.4 抽取器的实现

各级滤波器由MATLAB设计完毕后，具体的实现由verilog HDL代码来描述。先把将各级滤波器的代码写好，最后将各级滤波器实现整体级联，编写测试文件，在ModelSim进行仿真，观察输出波形图。从图8可以看到，clk为输入时钟，，clk_enable为输入使能信号，reset为复位信号，filter_in为输入信号，filter_out为输出信号，ce_out为输出提示信号。在输入信号作用下，每隔128个时钟周期信号对整体滤波器的输出信号filter_out进行一次赋值。也就是说，每隔一个时钟周期输入信号filter_in变化一次，每隔128个时钟周期才会有一个filter_out输出变化，显然，输入信号的频率是输出信号频率的128倍，也就是说对输入信号filter_in实现128倍抽取，整个系统达到128倍抽取的功能。这与我们想要实现的目的相吻合的。

图8 仿真波形图

3 结束语

文中介绍了CIC滤波器、HB滤波器、FIR滤波器和多相滤波器等多速率处理技术实现信号的抽取和内插，并通过MATLAB设计了一种多级抽取滤波器，通过verilog HDL代码实现该系统，最后在ModelSim进行仿真，验证了我们设计的正确性。