探讨初中数学解题教学中隐含条件的应用

江苏省启东市百杏中学 施晴花

数学问题通常由条件与结论两大部分构成，其中，条件是学生分析和解决问题的主要依据。不过在初中数学问题中，很多题目不仅有明确给出的条件，还有一些条件是隐藏的，并没有直接出示，这就是所谓的隐含条件。在初中数学解题教学中，教师需指导学生将题目中的隐含条件都挖掘出来，且做到合理应用，以扫除解题障碍，提高解题速度和正确率。

一、结合数学定义分析隐含条件

在解答初中数学题目过程中，部分题目的条件往往隐含在数学定义中，假如这些隐含条件被忽视，极易导致解题错误现象的出现。为此，在初中数学解题教学实践中，在解决有关定义的数学题目时，教师需引领学生结合数学定义着重挖掘题目中的隐含条件，利用定义中的隐含条件提升答案的准确性，以免在认识上存在缺陷，致使解题失误。

例如，在解一元二次方程时，教师设置题目：已知关于x的一元二次方程（n2-1）x2-（2n+1）x+1=0存在两个实数根，那么n的取值范围是什么？解析：在解答本道题目时，学生将会直接考虑到采用一元二次方程根的判别式，依据Δ=b2-4ac=[-（2n+1）]2-4（n2-1）=4n+5≥0，从而顺利求出答案为n≥-5/4。其实在解答问题过程中，将一元二次方程定义中ax2+bx+c=0（a≠0）的隐含条件“a≠0”所忽视，导致求出的n的取值范围不够完善。要想求出正确解答，还需结合一元二次方程的定义，根据n2-1≠0，可以得到n≠±1。所以n的取值范围是n≥-5/4且n≠±1。

针对上述案例，在解答有关数学定义的题目时，学生一定要充分考虑到定义中存在的隐含条件，并应用隐含条件求出完善的答案，提高解题的正确率，减少不必要失分现象的出现。

二、根据代数公式挖掘隐含条件

初中数学主要包括代数与几何两大部分，其中，代数由数和式构成，也是中考考试的重点考查范围，在解答部分数学题目时，一些条件往往隐含在代数公式中，学生极易忽视，从而出现解题失误。因此，在初中数学解题教学实践中，教师需要求学生关注题目中涉及的代数公式，深入发掘代数公式中的隐含条件，最终计算出完整的结果。

例如，教师可结合因式分解与一元二次方程精心设计这样一道题目：已知（m2＋n2）2－3（m2＋n2）－10＝0，那么m2＋n2是什么？解析：本道题是一道因式分解和一元二次方程相结合的题目，学生在解题过程中，极易想到采用换元法把m2＋n2设成x，则原方程转变为x2－3x－10＝0，再利用因式分解法可以快速求出答案：x=5或x=-2，即m2+n2=5或m2＋n2=-2。这样的结果显然是不正确的，原因是学生忽视了代数公式m2+n2不能是负数这一隐含条件，所以正确答案需要将m2+n2=-2这一情况排除掉，通过对代数公式知识的应用，最终答案是只能取m2+n2=5这一情况。

在上述案例中，学生在解答该类数学题目时，一定要注意深入发掘代数公式中的隐含条件，通过知识的应用将解题过程完善，把错误结果排除，以免因忽视隐含条件导致计算错误。

三、利用几何图形找出隐含条件

几何是初中数学课程的组成部分之一，主要是有关图形方面的知识，同样是中考考试中的重点。在初中数学解题教学中，针对解答与证明类的几何问题，教师需指导学生灵活运用数形结合思想，不仅需标注出题目中的已知条件，还要认真观察几何图形，目的是找出和应用图形中的隐含条件，为解题彻底扫除障碍和铺垫道路。

比如，在图1中有矩形纸片ABCD，先折出折痕BD，再折叠，让AD边与对角线BD重合，得出折痕DE，假如矩形的长是2，宽是1，那么AE的长是多少？

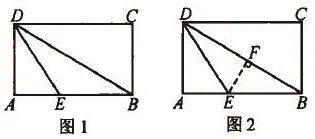
解析：本道题目看起来十分简单，只需利用勾股定理就能够轻松求出AE的长度，不过仔细研究发现，为求出AE的长度，首先需要计算出DE的长度，但是DE的长度是未知的，也无法通过计算直接求出，导致解题遇到障碍，原因是学生没有发现DE是∠ABD的角平分线这一隐含条件。找到之后，如图2，过点E作EF垂直BD于F，那么AE=EF，将求AE的长度转变为求EF的长度，根据题意得出之后再利用勾股定理在Rt△BEF中求出EF的长度，即AE的长。

如此，在解答几何类数学题目时，学生要通过数形结合思想的应用找出隐含条件，补充题目中的已知条件，这样解题条件才齐全，既可以锻炼他们对数学思想的应用，还有利于解题。

在初中数学解题教学活动中，隐含条件对解题来说具有重要作用，在解题过程中只有认真分析和仔细观察，才能够发现隐含条件，通过合理应用确定简单明了的解题思路，让学生在解题中事半功倍、得心应手，提高他们的解题效率。