利用翻折手段认知几何体模型

江苏省常州市三河口高级中学 胡爱华

众所周知，立体几何是培养学生空间想象能力的重要章节，而翻折问题又是立体几何中极具想象能力的问题类型，其以平面图形为根本，以动态转动为背景，将空间想象能力的考查融入问题之中，做到了平面几何和空间几何之间的知识交替，提升了学生空间感知的区分，从而提升了学生直观想象的学科素养。

一、概念认知——认知空间四边形

空间几何是三维的，从翻折的角度来说，空间几何可以看成是平面几何的升级。比如，平面四边形和空间四边形是怎么区别的？不少学生对于这样的数学概念是缺乏认知的，教材中也恰恰对很多几何概念的描述有所缺失。举一个很简单的案例：四面体的概念认知，教材中并没有明确给出一些几何体的概念，如空间四边形、四面体等等，只是零星提及，这让学生认识几何体概念是模棱两可的。用平面几何中的四边形ABCD为载体，通过翻折逐一介绍，可提升学生对基本概念的认识程度。

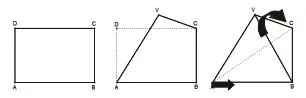
图1

如图1，以四边形ABCD沿着对角线AC进行翻折，记其在空间的位置为V，此时由空间几何的公理可知，其四条边不在同一个平面中，此时平面四边形就转变成空间四边形了。进一步思考四面体概念和三棱锥概念，将空间四边形的AC、VB进行连接，从几何体结构的角度来说，这就是我们熟悉的三棱锥；从多面体面数的角度来说，这就是我们熟知的四面体。因此可以这样认为：其实这四个在空间的点组成的几何体，即{三棱锥}={四面体}={空间四边形}。那么我们进一步想：为什么四棱锥不等同于五面体，五棱锥不等同于六面体了呢？这就很容易解释了，因为五面体除了四棱锥之外，三棱柱也可以，因此这种等价命名方式就不可取了，同理，六面体也可能是某一种四棱柱，而不仅仅是五棱锥了。通过简单的翻折，学生对平面四边形如何形成空间四边形有了足够的认识，对概念为什么如此称呼有了更为深刻的认知，将翻折手段用于概念教学，有助于学生对于空间概念的感知。

二、定性感知——认知圆锥模型

定性的空间翻折问题，是一种非精确量化的立体几何问题，这里更是进一步对学生空间想象能力的培养。如何解决定性的翻折问题，这里笔者以为需要两种主要手段或工具，其一是模型的帮助，在问题解决过程中制造模型，加强公理化体系在模型中的运用；其二是向量知识的帮助，向量是很好的解决空间几何的工具，尤其是以基底为载体的自由向量。

（1）存在某个位置，使得直线AC与直线BD垂直；

（2）存在某个位置，使得直线AB与直线CD垂直；

（3）存在某个位置，使得直线AD与直线BC垂直；

（4）对任意位置，直线“AC与BD”“AB与CD”“AD与BC”均不垂直。

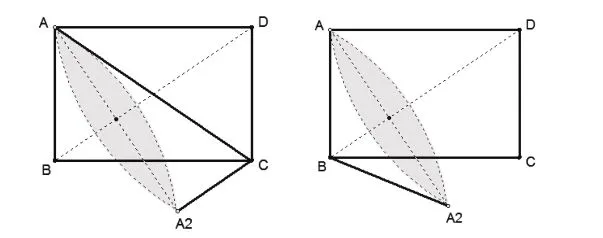
图2

分析：笔者以为解决本题有两种主要方式，其一是制作纸张模型，结合公理化体系论证，但是违背了“小题小做”的意愿；其二是自由向量的手段，在翻折问题的感性认知上可以做到游刃有余。

首先揭示本题翻折的本质，即△ABD沿矩形的对角线BD所在的直线进行翻折过程中，其中，点A的轨迹自然是阴影部分（如图2）底面圆周上的点。以自由向量呈现的夹角状态做出感性的分析：

我们发现，翻折过程中对于动点A的轨迹的认知，是问题的模型本质，即圆锥模型。小题小做的方式告诉我们，用向量的工具性作用大大简化了翻折问题的思考，在头脑中有了感性的角度认知，高效简洁。

总之，空间几何中的翻折问题是提升空间感知的重要问题载体，通过其熟知基本几何体的形成、感知并解决问题是教学需要加以关注的，进一步可以利用翻折问题加强空间想象能力的培养，这才是翻折问题教学实际的价值所在。