数学解题思维程序设计初探

湖北教育出版社 孙 昕

在数学学习过程中，学生常在解题时对审题、探索问题的解决方案、习题的表达方式以及解题方法经验的总结存在一定的困难。那么，学生在解题中除了总结基础知识、基本解题方法外，还应有哪些方面的突破呢？基于此，笔者提出按照解题思维程序，理清解题思路，构建正确的解题思维过程，达到又快又好地解题的目的。

一、解题思维程序的构建设想

通常来说，解题思维可分为：认真审题、积极探索、准确表达、反思总结这四步。其中，认真审题和积极探索是重难点，反思总结则常常被忽略。中学生解题遇到阻碍的主要原因大多是未形成良好的思维习惯。

审题一方面要寻找题目的关键字词，另一方面要对问题的条件与结论进行适当的分解、整合，促使其向已知问题转化。探索则常从目标或结论出发分析条件，运用相关数学知识和方法联通条件与目标，建立题目条件与目标结论间的桥梁。反思总结是对结论进行验证，对解题方法进行归纳，并思考有没有其他途径和方法，使解题方法系统化。只要将解题的思维过程适当分拆，形成明确的解题思维程序，便可帮助学生形成较好的解题习惯。根据中学数学解题思维特点，设计数学解题思维程序如下：

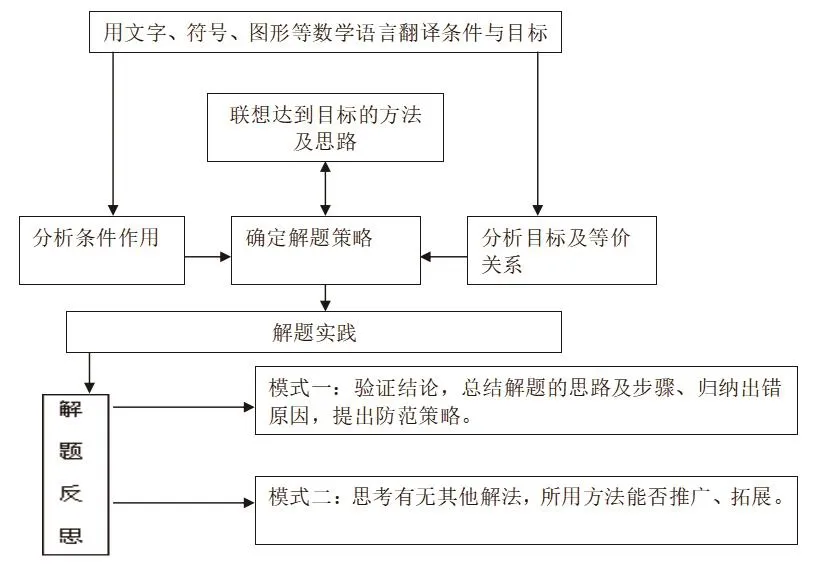
二、解题思维程序的实践尝试

在解题过程中利用解题思维程序，寻找已知与目标之间的关系，并通过反思总结拓展和巩固解题思路、方法。

分析目标：求实数a的取值范围。

方法探索：要求不等式中实数a的取值范围，可从解不等式着手。

策略分析：若从解关于x的不等式入手，不易联通条件与结论。分析结论“求a的范围”，将不等式看成关于a的不等式，再解这个不等式。

归纳总结：本题先分析题目条件及目标，将条件与目标结论用符号语言表达出来，再从条件与目标间的关联探索解题方法与策略，将关于x的不等式转化成关于a的不等式，得到a的取值范围后，用特殊值来验证，发现与题意不符，于是探索隐含条件得到正确答案。因此，在解题过程中，条件向目标结论转换时应注意等价性。

评注：在解决本题过程中，思维程序起到积极的引导作用，运用解题程序寻找题目的突破口，找出条件与结论的联结点，通过验证纠正了错误。解题思维程序中强调验证、归纳，是由于这两个步骤在学生解题过程中常常是被忽视的，而缺少这些步骤一方面容易导致解题不完整，另一方面，缺少归纳也难以及时总结解题经验与方法。

解题思维程序的应用，为学生思考数学问题提供了一个操作较强的思维流向，使学生在该程序的引导下，一步步接近问题的中心，展开解题实践。解题思维程序强调学生的反思和归纳，在有意识的反思归纳中不断提高数学思想方法的运用能力，学生在遇到类似的问题时能熟练运用知识迁移，形成解题思维程序。

三、解题思维程序的教学特性

实施解题思维程序教学前，教师要做好准备工作，除了帮助学生养成良好的解题思维程序习惯外，在解题思维程序教学中还要把握以下几点：

1．主体性

要充分体现以学生为主体，教师为主导的原则，让学生有一定的思考时间和空间，引导学生暴露思维受阻的原因，由学生自主归纳解题要领。

2．启发性

在确定解题策略时，学生可能产生各种想法和思路，要启发他们表达出来。创设思维的良好环境，并引导学生进行反思，使学生在运用解题技巧和方法时有所突破。

3．循序渐进性

让学生养成运用思维程序解题的习惯。教师可以通过设问来引导学生领悟思维程序的各个要素与步骤，逐步放手，培养学生良好的解题思维习惯。

4．系统性

解题思维程序重在探索和反思，教师应通过总结归纳帮助学生形成系统完整的知识结构，培养学生思维的独创性和批判性。

解题教学中，应注意思维程序的灵活运用，并不是所有题目都能用该程序来思考、解决。根据题目的具体情况可适当增减，顺序也可调换或交叉。关键是在程序的帮助下，学生思考的方向变得有序，验证、归纳成为自觉行为，从而有效地提高解题水平。