基于FAHP的水下目标多源探测仿真系统评估*

张 森，金 超，孙力帆，卜文绍

（河南科技大学信息工程学院，河南 洛阳 471023）

0 引言

仿真可信度是仿真系统的一个重要指标，仿真可信度评估是在仿真系统建模的过程中必不可少的环节［1］。开展可信度评估工作有利于促进水下目标探测仿真技术的发展，提高水下目标探测仿真结果的准确性，降低应用风险，保证仿真系统质量，促进对水下目标探测技术的深入研究。

自20世纪80年代以来，飞速发展的高新技术使得水下目标探测技术有了长足的发展，延伸出了多种探测方式用于水下目标的探测。海洋环境复杂多变，水下目标也具有不同的属性，单一探测方式的探测系统很难全面提取水下目标的信息，综合多种方式用于水下目标探测已是未来发展的趋势。董庆亮［2］综合利用多波束测量数据和侧扫声纳声像图进行海底目标的探测，有效增强了不同设备之间的互补性，提高了探测质量。丁鑫同［3］建立热尾流探测、激光雷达探测以及磁异常探测3种非声探测模型，对底层探测信息进行融合处理，得到潜艇探测仿真结果。但是仿真结果依赖于仿真系统的可信性，且暂未查到有关水下目标多源探测仿真系统评估方法的相关文献。因此，急需提出一种适用于水下目标多源探测仿真系统的评估方法。

FAHP因其定性与定量相结合的特点，被广泛应用于众多领域的评估之中。Wu Q等［4］建立了水下机器人的整体性能评估系统，通过FAHP得到评价指标的权重系数，能够客观地反映机器人的整体性能。Wang B等［5］利用FAHP解决了高校科研项目管理绩效评估的问题。Lin C等［6］运用FAHP对不同服饰设计方案进行评估，计算各方案的权值，得到最佳的服装设计方案。刘瑛等［7］使用关键点划分飞行器机动动作，运用FAHP确定不同关键点的权重，实现飞行器机动动作风险的定量评估。

为了提高水下目标多源探测仿真系统的应用水平，推进水下目标多源探测仿真工作，本文沿用上述文献的思想，提出一套基于水下目标多源探测仿真系统的评估指标体系，运用FAHP得到各层指标权重，作为探索性研究，为水下目标多源探测仿真系统评估工作的展开提供基础性指导理论。

1 水下目标多源探测仿真系统

UMESII型系统是本课题组研发的第二代基于HLA（High Level Architecture）技术的分布式水下目标多源探测仿真系统。该系统的主导思想是通过搭建分布式交互平台，开发出主/被动探测元与载体、目标及环境节点，实现对同一时空条件下多类多元多型多维探测信息的实时获取、处理及智能识别，解决水下目标多源探测系统的仿真问题。UMESII型系统组成图如图1所示。

本应用系统的主要实体模型及其功能：声纳是声波信号发射装置，发射一定频率、波长的声信号脉冲来探测水下目标。水听器是声波信号接收装置，接收来自目标反射回的水声信号，并转化为易于处理的电信号。光源是光波发射装置，发射一定频率、波长的光信号脉冲来探测水下目标。CCD是光波信号接收装置，接收来自目标反射回的光信号。磁力仪是一种高精度磁场探测装置，能够探测海洋中因铁磁物质在磁场中作用而引发的磁异常。

2 仿真系统可信度评估方法

对水下目标多源探测仿真系统的可信度考量，需要全面分析系统内各因素U对总体可信目标O的影响尺度，由于指标是人为划分的，难免忽略了系统元素之间的耦合特性，所以需要用模糊评判法对指标进行综合优化以削弱系统误差，故评估方法优先采用FAHP。该方法既有效地综合了评估专家的意见，又充分体现了仿真系统可信性评估过程所具有的模糊性，减少了因个人主观因素而带来的风险。

2.1 三角模糊数及模糊综合程度值

定义1 如果M是一个三角模糊数，则它的隶属度函数为：

其中 l≤m≤r，{x∈R|l＜x＜r}，三角模糊数 M 可记为M=（l，m，r）。

定义 2 设三角模糊数 M1和 M2，M1=（l1，m1，r1），M2=（l2，m2，r2），M1≥M2的可能程度为：

2.2 FAHP的主要步骤

Step 1 根据系统的仿真目的，运用层次分析法对物理系统进行逐层建模，建立系统层次结构模型。

Step 2 根据层次结构模型中的各层指标，针对指标对仿真系统可信度总体目标O的重要性，由n位专家依据经验对各评价指标的权重进行两两比较打分，用三角模糊数构造两两判断矩阵A=（aij）n×n。其中比较尺度aij=（lij，mij，rij），表示Ui相比Uj对目标O的重要程度，则反向比较尺度aji=（1/rij，1/mij，1/lij）。为了减少因过多选择增加评估过程中的不确定性和人为误差，根据重要性对aij的取值化为1～9共9个尺度，其中用 M1、M3、M5、M7、M9分别 1、3、5、7、9，而 M2、M4、M6、M8代表中间值 2、4、6、8，如表 1 所示。

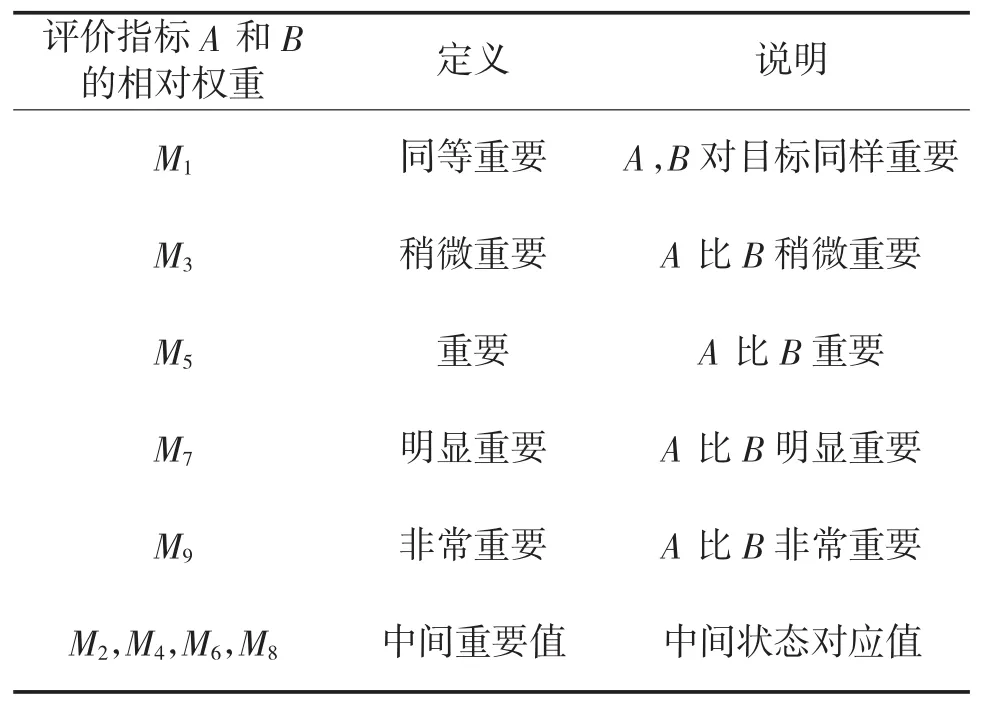
表1 相对权重评判表

Step 3 对A中所有元素进行算术平均处理，得到新矩阵A'。对n位专家的三角模糊数进行平均后得到：

为了进一步降低因个人主观臆断、理论知识或个人喜好等诸多人为因素带来的主观性误差，设置置信区间，在式（3）得到平均三角模糊数M'后，令其与原始三角模糊数M进行比较。当原始三角模糊数M与平均三角模糊数M'的差值在置信区间内时，认为结论可信；当原始三角模糊数M与平均三角模糊数M'的差值不在置信区间内时，要舍弃该专家评判数据，重新根据式（3）进行计算，得到的新的平均三角模糊数M''。三角模糊数的取值范围为1/9～9，选取的都是水下探测领域的专家，本文取值范围的1/4，即作为置信区间。

Step 4 计算其中各个元素的综合程度Mi。根据矩阵A'中第i个对象满足第j个目标的程度值为aij'，由此可得第i个对象关于n个目标的综合程度值。

Step 5 计算仿真系统各层指标的权重向量。

定义3 一个模糊函数比其余n个模糊函数Mi（i=1，2，…，n）大的可能程度是：

Step 6 根据各层指标的权重向量以及可信度得到整体仿真系统的可信度，其中上层指标可信度是由下层指标逐层向上加权得到。

3 仿真系统评估

3.1 仿真系统评估指标体系

本文在大量仿真系统研发以及仿真系统评估研究的基础上，结合仿真系统VV&A理论，针对水下目标多源探测系统建模中存在的整体关联性、结构层次性和动态适应性等复杂性问题，运用FAHP提出一套水下目标多源探测仿真系统可信度层次化指标体系，如图2所示。

3.2 确定各级指标权重

依据章节2和3.1中所提出的水下目标多源探测指标方法及体系，对于 U1，U2，U3，U44 个一级指标，请3位专家对其权重进行打分，得到的两两判断矩阵见表2，表中的纵横坐标分别代表图2中的影响指标因素。

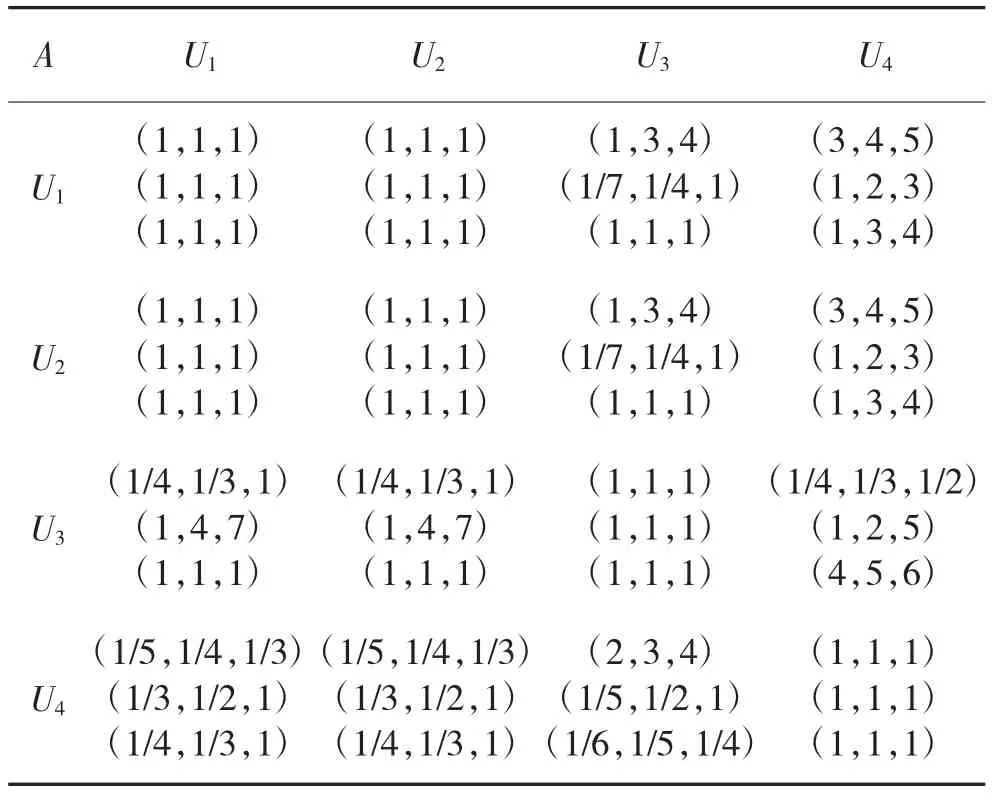
表2 一级指标三角模糊判断矩阵

根据Step3可得模糊一致判断矩阵A'见表3：

由式（4）可得初始权重为：

由式（5）可得：

同理可得：d（U2）=1，d（U3）=0.993 4，d（U4）=0.531 5。

归一化后可得权重向量为：

同理可以得到二级指标的权重，整理后水下目标多源探测仿真系统各级指标权重如表4所示。

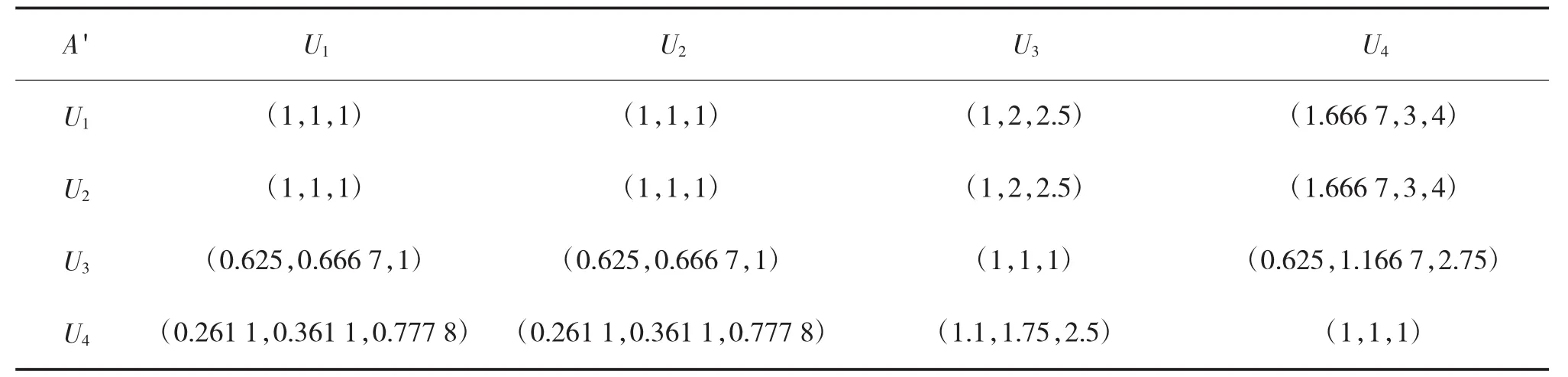
表3 一级指标模糊一致判断矩阵

表4 仿真可信度各指标权重

3.3 可信性分析

组织10位专家对UMESII型水下目标多源探测仿真系统的各层指标进行打分，得到评估矩阵。其中仿真模型的子指标得到的结果如表5所示。

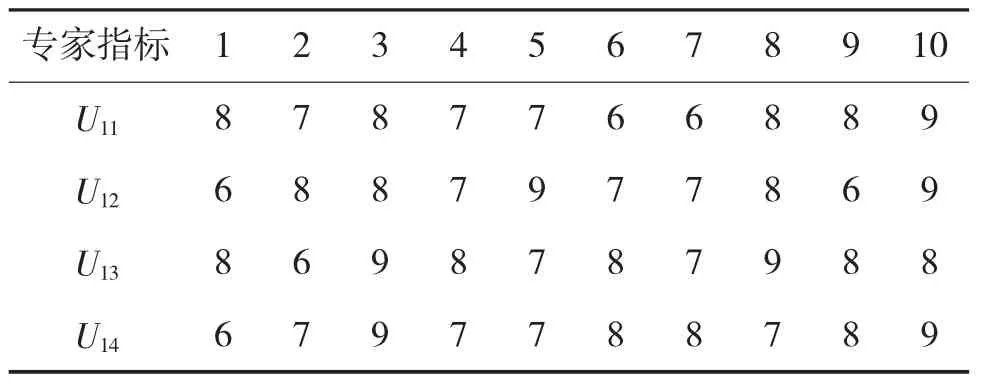
表5 仿真模型子指标权重评价

由此得到评价矩阵R为：

因此，综合评估结果为：

同理可得：

综合上述子指标评估结果，得到UMESII型水下目标多源探测仿真系统的评估向量为：

为了便于评价，使结果更为清晰，用百分制为各评价等级赋值：从“最差”到“最好”9个级别分别赋值为20～100，可得UMESII型仿真系统的综合评价得分为：

H=（0 0 0 0 0 0.149 4 0.349 4 0.377 4 0.123 8）·（20 30 40 50 60 70 80 90 100）=84.756

评价结果表明，该仿真系统具有较高的可信度，能较好地模拟真实水下目标探测系统。

本方法是一种首次针对水下目标多源探测仿真系统的可信度评估方法。参考并对比其他仿真系统的评估方法，分析结果体现以下3个方面：

1）文献［4-7］中的方法只针对某特定系统建立了评估指标，不具有通用性，没有对应的水下目标探测仿真系统具体指标体系可供参考，故评估方法不能横向对比。

2）对比文献［8］中的方法，本文所使用的方法有更强的适用性，并且能够利用模糊处理削弱人为干扰误差，因此，本文的可信度评估方法更加科学合理。

3）文献［9］中的方法可以参考，经比较，与本文评估方法所得结论基本一致，因此，本文所提出的可信度评估方法可行可靠。

4 结论

本文针对水下探测的探测方式多样性和海洋环境复杂性等特点，结合仿真系统VV&A理论，提出一套适用于水下目标多源探测仿真系统的评估指标体系，运用模糊层次分析法，分析了影响仿真可信度总体目标的各因素权重，初步探讨了水下目标多源探测系统仿真评估方法。并以UMESII型系统为例，实现了理论方法在工程实践中的应用探索，能够完成对水下目标多源探测仿真系统［10-11］的可信度评估工作。

在此基础上，本文提出水下目标多源探测仿真系统的评估应遵循以下原则：

1）为了减少因个人主观臆断带来的评判误差，对综合评判打分专家进行两点要求：必须保证是相关领域的专家，避免因专业知识的缺乏而导致的误差；评判专家人数不得低于3人，避免因个人偏好而引起的误差。

2）针对仿真系统的差异和评审专家的专业水平层次选取合适的置信区间，本文以打分区间的1/4作为置信区间，可以根据不同情况适当调整。

3）增加评估方法的普适性。在满足仿真系统评估准确性的基础上，能够适用于其他水下目标多源探测仿真系统的评估工作。