一种提高软件可靠性验证测试效率的方法*

马振宇，刘福胜，吴 纬，陈守华，韩 坤

（1.陆军装甲兵学院，北京 100072；2.北京特种车辆研究所，北京 100072）

0 引言

当今软件在各个领域当中，被使用的范围越来越广泛，其自身的可靠性问题也就成为专家学者们越来越关注的问题。尤其在武器装备、航空航天等相关领域，对于这些安全关键型的软件，使用方明确给出了软件可靠性指标要求。那么如何高效、客观地验证这一类安全关键型软件的可靠性是否达到用户所规定的可靠性标准，成为当下软件可靠性验证测试［1］中最关键的问题。

目前针对软件可靠性验证测试有一类关于使用贝叶斯方法的测试方法。文献［2］应用了构造共轭分布的贝叶斯方法。文献［3］提出了基于先验动态整合的可靠性验证测试方法。文献［4］提出了基于混合贝塔分布的贝叶斯验证方法。文献［5］应用了基于减函数的先验分布构造法进行测试验证的方案。进一步在文献［6］中，提出了基于减函数的多层贝叶斯软件可靠性验证测试方法。

为了更好地利用先验信息，找到新旧软件产品之间存在的差异，更加真实地反映软件可靠性验证测试的实际结果。本文首先采用了混合加权贝叶斯方法，通过引入混合加权权重（继承因子），充分考虑软件在更新换代中各类信息，将混合加权权重看作一个随机变量，提出了基于混合加权贝叶斯的软件可靠性验证测试方法。接着详细给出了在混合加权情况条件下的超参数估计方法。最后通过实验分析，验证了该方法的有效性。

1 贝叶斯验证测试方法基础理论

1.1 贝叶斯方法的基本原理

将每一次软件可靠性验证测试试验看成成败型试验，同时设定每次软件被测试出失效的概率相等且为p，并且每一次测试均符合n重伯努利实验。那么在n次独立重复测试中，出现X次失效次数的概率就符合二项分布，即：

根据上述假设的条件，在实际的软件可靠性测试中，选择共轭分布贝塔分布作为失效概率的概率密度函数的先验分布。同时后验分布应与先验分布属于同一类分布。

其中，00，b>0，a，b 都为先验分布的超参数。B（a，b）为贝塔函数，即：

依据式（2），软件经过n个测试用例遍历测试完成之后，出现了r个失效数，并由贝叶斯定理可以得到该失效概率的后验分布应是 Beta（a+r，b+n-r），即：

在进行软件可靠性验证测试时，假设初始的可靠性指标为（p0，c），其中 p0为软件失效概率，c为置信度。联合式（4）求出满足下式中最小的整数解，即为软件可靠性验证测试的测试用例数n。

1.2 超参数的求解办法

根据历史性数据结合贝叶斯推断原理对先验分布进行估计，即对超参数a、b进行量化估计。其求解的基本原理为：假定样本数（x1，x2，…，xn），对变量p 的似然分布为 g（x1，x2，…，xn|p），并且变量 p 的先验分布为f（p），则可得到样本数据和变量之间的联合密度函数f（p）g（x1，x2，…，xn|p），进而求得样本的边缘密度函数。h（x1，x2，…，xn）的估计是通过历史样本数据得到的，然后将确定出的f（p）和g（x1，x2，…，xn|p）一同去估计出超参数的值。

依据超参数的求解原理，选用软件在以往测试过程中遗留下的最后m组的测试记录作为先验信息，每一组里含有n个测试用例，并同时统计出每一组测试用例中造成软件失效的数量，分别记作k1，k2，…，km，因而求得失效概率的经验值为ti=ki/n（i=1，2，…，m）。

样本的边缘分布为：

进而求得h（x）对应的一阶矩为：

h（x）的二阶矩为：

将 E（x）、E（x2）记作 w1、w2，则超参数 a，b 为：

然而w1、w2可以通过经验样本值的期望所估计，即：

把式（10）代入到式（9）中，即可估计出超参数a与b的值。

2 混合贝叶斯方法

2.1 混合贝叶斯基础理论

通常来说，软件的研发过程是一个不断更新的进程。高版本的软件一般是在低版本的软件基础之上进行改进的，因此，高版本的软件就会具有许多和低版本软件相似的特性，同时高版本的软件也会具有自己独有的特性。这就要求先验分布既有传承性，还有由于版本的升级换代引发的不确定性。因此，本文引入混合先验分布的概念，把混合加权权重［7］（继承因子和更新因子）结合到先验贝塔分布当中去，使得软件可靠性验证测试方案更具有实际意义。

在二项分布中，混合先验分布为：

其中：ρ为混合加权权重（继承因子），1-ρ为更新因子，0≤ρ≤1。p 为失效概率，0＜p＜1。a，b 为超参数。

根据式（11）可以得出，混合先验分布是无信息先验分布以及共轭先验分布的加权和。继承因子体现了历史数据符合总体与试验样本符合总体的相似程度，然而更新因子就体现出更新的高版本软件中带来的可靠性不确定性。

当ρ=1时，说明高版本软件对低版本软件没有进行任何的改进措施，那么此时的混合先验分布就是共轭先验分布，即为f（p）=Beta（a，b）；当ρ=0时，说明高版本软件彻底改变了低版本软件的所有性质，是一个全新的软件，那么此时的混合先验分布就是在区间［0，1］上的均匀分布，即f（p）=1。实际的意思就是彻底没有利用历史信息，在无先验信息的条件下，确定的先验分布；当0＜ρ＜1说明高版本软件与低版本软件是类似的，历史数据起到了一定的参考价值。当ρ取值在0和1之间，也更贴近实际的工程意义。

因为继承因子对软件可靠性的验证起到了至关重要的作用，所以对于它的取值就应该非常慎重。它体现的是相似程度。如果当高版本软件在低版本软件的基础上做了许多改动，则ρ的值就应该越小；反过来说，如果当高版本软件在低版本软件的基础上几乎没有做太多的改动，则ρ的值就应该越大。

2.2 混合加权权重下的超参数估计方法

依旧根据超参数估计的基本原理，结合式（6）与式（11），可以得到在混合加权贝叶斯条件下的样本边缘分布，即：

结合式（7）和式（11），求得在混合加权贝叶斯条件下的h（x）对应的一阶矩为：

同理，结合式（8）和式（11），求得在混合加权贝叶斯条件下的h（x）对应的二阶矩为：

接着把式（10）代入到式（15）中，即可估计出超参数a与b的值。

3 基于混合加权贝叶斯的验证方法

在软件可靠性测试过程中，用n个测试用例进行遍历测试，共出现了r次失效。再根据混合贝叶斯的先验分布，结合式（1）和式（11），可以推导出失效概率的后验分布，即：

根据实际情况，设定软件可靠性测试中最大失效的次数r，失效概率为p0，置信度为c。应用式（16），求出满足式（17）的最小整数值，也就是基于混合加权贝叶斯可靠性验证测试方案的测试用例数量n。

4 案例分析

本文通过一个实测项目结果用于证明基于混合加权贝叶斯方法在软件可靠性验证测试的方法中有效地降低工作量，减少测试用例的数量。首先收集软件可靠性测试过程中最后10组数据作为估计先验信息的历史数据，每一组出现的失效次数如表1所示。

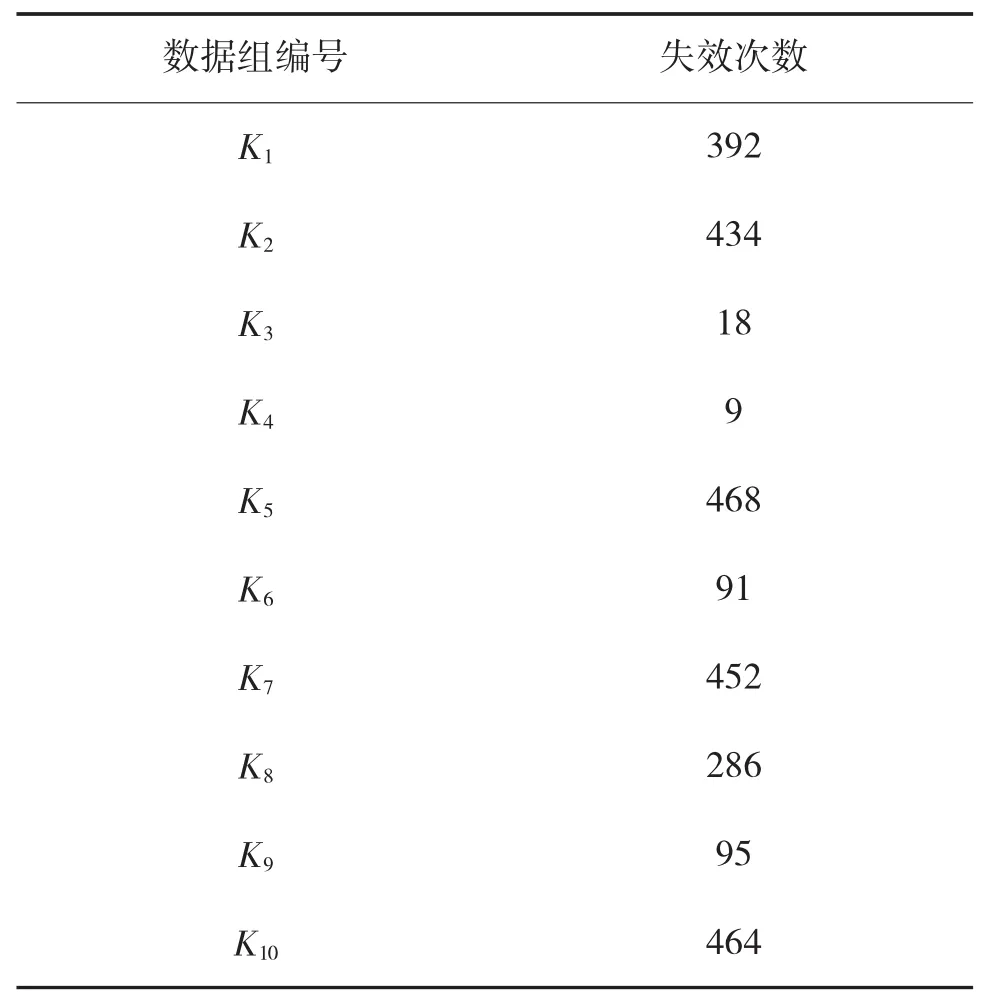
表1 先验信息失效数据

由式（15）可以算出在不同混合加权权重下的先验分布的超参数的估计值，如表2所示。

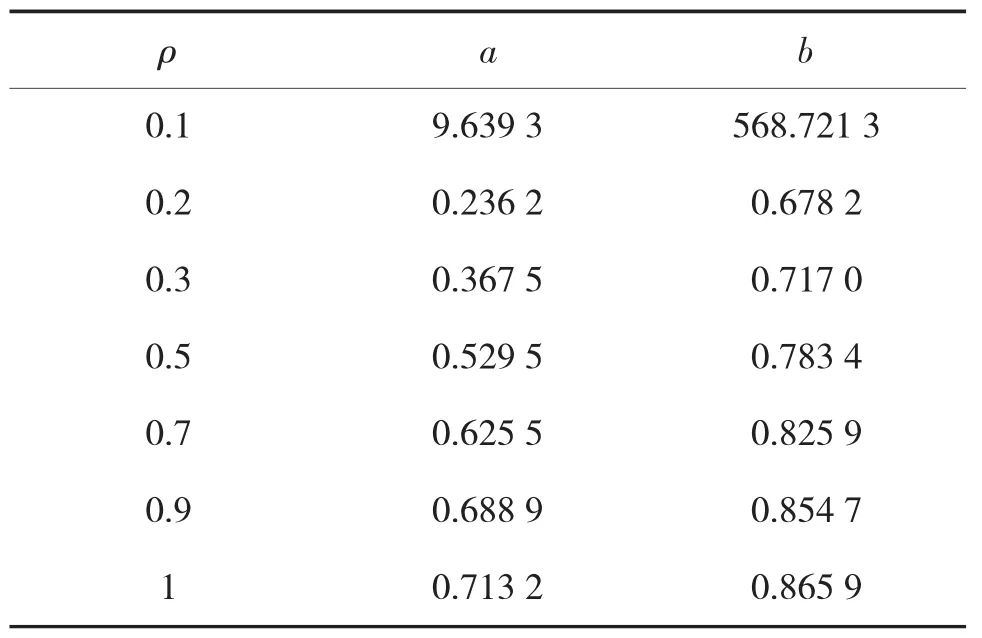
表2 不同混合加权权重下的超参数估计值

特别指出，表2中并未包含ρ=0时，超参数的估计情况，那是因为当ρ=0时，此时为无先验信息的分布，并且该分布为在区间［0，1］上的均匀分布，同时满足 Beta（1，1）=U（0，1）。也就说明此时 a、b 的取值都为1。

给定测试方案的指标（p0，c）=（0.001，0.99），即为在置信度为0，99，失效概率为0.001。同时规定最大允许失效次数为5的条件下，通过历史信息，结合式（17）求得在不同失效个数下，不同权重测试方案所需要的测试用例数量，如表3所示。

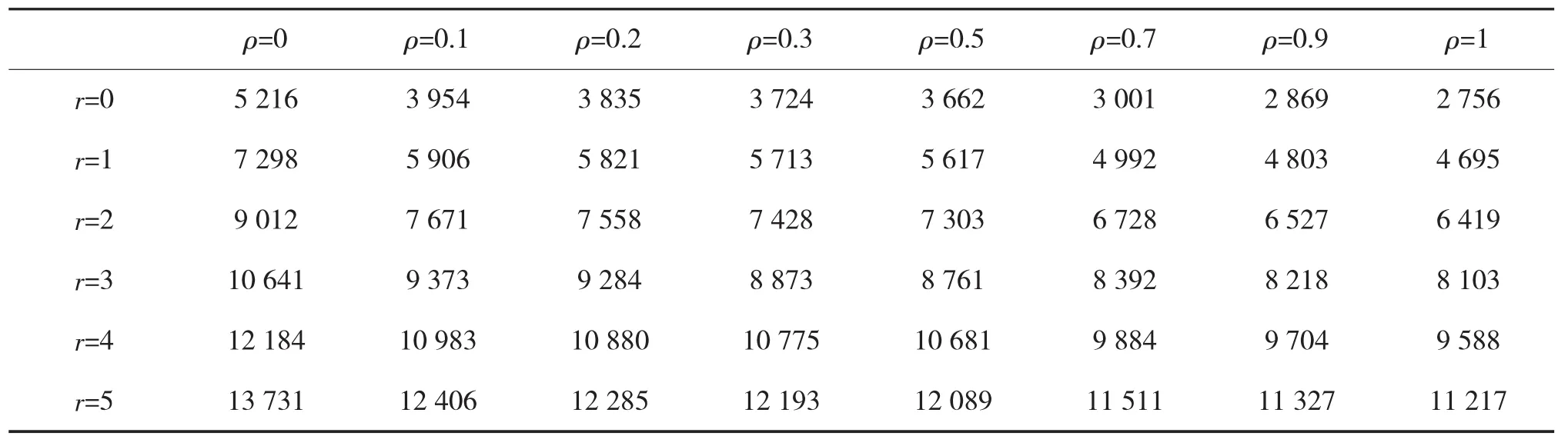
表3 基于混合加权贝叶斯验证方法所需测试用例数量

根据表3，可以得到以下2个相关结论：

1）当高版本软件在低版本的基础上做出的改变越多，那么混合加权权重的值就越小，这就造成软件可靠性验证测试的测试用例数量陡然增加；反之，高版本软件在原有软件的基础上只做出少许改变，则混合加权权重的值就越大，对于测试方案所需要的测试用例数量来说，增加的测试用例数量也就没有那么明显。特别指出当ρ≤0.5时，软件可靠性验证测试方案的测试用例数会大幅度增加，因此，本文推断存在当高版本软件在原软件基础之上做出至少一半的改动时，就会给验证测试带来巨大的工作量，增加测试成本。

2）当ρ=0时，说明此时是在无先验信息条件下，测试方案对于验证测试所需要的工作量是最大的。当ρ=0.1时，可以发现较ρ=0的条件下的所需测试用例数减少了许多。这是因为当ρ>0时，说明是在有历史数据，先验信息的情况下，可以显著地降低验证测试的工作量。贝叶斯方法的测试方案比起无先验信息的测试方案分别在失效数r=0，1，2，3，4，5 时，测试用例最少分别减少了 1 262 个、1 392个、1 341个、1 268个、1 201个、1 325个（ρ=0.1时），最多减少了2 460个、2 603个、2 593个、2 538个、2 596个、2 514个（ρ=1时）。

5 结论

本文首先提出基于贝叶斯方法的软件可靠性验证测试方案，并同时给出针对超参数求解的详细推导过程。接着提出混合加权权重，该权重能够更加真实地反映软件在更新换代过程中的各种变化信息。然后依据超参数的求解过程，给出了混合加权情况下的超参数估计的具体方法。最后给出了提高软件可靠性验证测试效率的方法。通过案例分析，该方法比起传统贝叶斯方法更客观地反映被测软件的可靠性，因此，该方法在实际运用过程中更加合理化。同时比起无先验信息的测试方案，在保证验证结果置信度不变的基础之上，能够显著地降低可靠性验证测试所需要的测试用例数量。但是该方法还需要投入到今后大量的验证测试实验中去检验，以此来不断完善该方法，以便后续更高效地应用到软件可靠性验证测试中。