缺失数据下基于直觉模糊的动态威胁评估*

孙 宁，冯 琦，高晓光，刘 超

（1.西北工业大学电子信息学院，西安 710129；2.中国飞行试验研究院，西安 710089）

0 引言

空战威胁评估是空战指挥决策的依据，也是战场信息融合的重要环节，合理有效的威胁评估结果对目标分配及火力分配阶段起重要作用，也是提高作战效能的关键。传统的威胁评估方法［1-2］只根据某一时刻点所收集到的目标威胁信息进行评估，同时需要威胁信息完善而精准，亦称静态威胁评估方法。随着空战节奏的加快、战机机动性变强，为适应空战动态性特点，需要依据多个时刻点威胁信息的动态评估方法。而动态评估方法对机载电子系统获取威胁信息的实时性要求非常高，即要求对这些信息迅速作出判断、处理和决策，这无疑增加了机载传感器收集目标数据信息的不确定性，甚至导致有些时刻数据的缺失，无法得到较为完整的实时威胁信息。

基于以上分析，本文提出一种基于直觉模糊集的动态空战威胁评估方法。为体现不同时间点威胁信息重要程度的不同，采用泊松分布法给时间序列赋权；为解决某些时刻点的数据缺失问题，采用诱导有序加权平均（IOWA）算子［4］的空值估计算法实现缺失数据的补齐；为体现决策者的主观意愿和数据信息的客观性，采用主、客观赋权方法相结合来确定目标属性的权重；最后将TOPSIS方法［5］运用到直觉模糊集中，通过直觉模糊TOPSIS方法建立动态空战多目标威胁评估的数学模型。不仅有效解决了缺失数据下传统的评估方法难以处理的问题，也反映了整个空战态势的动态变化过程。

1 目标属性的直觉模糊集描述方法

1.1 直觉模糊集

式中，uA（x）和 vA（x）为 A 的隶属度函数和非隶属度函数。对于论域X上的直觉模糊集A，称为A中元素x的犹豫度。

1.2 目标属性矩阵

影响目标威胁程度的因素有很多，本文中选取空战能力因子、角度威胁因子、距离威胁因子和速度威胁因子［2］作为空战威胁评估目标属性。

设在空战过程中遭遇m架敌机，每架敌机具有n个属性，即目标集为，属性集为。

1.2.1 定性属性

对于空战能力因子通过语言变量值对目标空战能力进行描述，对应的直觉模糊集如表1所示。

表1 空战能力语言变量值与直觉模糊集对应关系

1.2.2 定量属性

实际空战中，目标速度越大，则速度威胁就越大；目标的角度和距离越小，角度和距离的威胁因子就越大。因此，速度威胁因子的隶属度与非隶属度计算公式为：

角度威胁因子和距离威胁因子的隶属度与非隶属度计算公式为；

2 基于IOWA算子的空值估计算法

目标威胁信息的不确定甚至缺失无疑会增加威胁评估的难度，甚至导致重大的错误决策。待缺失数据补齐后再进行威胁评估是一种合理的解决方案。常用的缺失数据补齐算法有：Mean Completer（MC）估算法［6］、Combinatorial Completer（CC）估算法［7］、K-means Clustering（KMC）估算法［8］、EM 估算法［9］等。MC估算法和CC估算法效率较低，数据量大时，这两类算法代价太大；KMC估算法分类数不易确定，且易陷入局部最优；EM算法需要知道数据满足的分布，显然空战动态信息不可能时时确定数据分布类型。

采用IOWA算子的空值估计算法既考虑到了对象之间的相关性，又考虑了属性之间的相关性，并且可以根据不同背景调整权重向量，将其运用到直觉模糊理论中，可很好地补齐目标缺失数据。

现给出如下假设：

设某一空战初始决策数据信息表S0，目标集为，属性集为。在属性ai上都有取值的对象集为NAi0，在属性ai的相关属性aj上都有取值的对象集为RAi0，含有空值的属性集为MA0，经过r次迭代得到信息系统为Sr，在属性ai上都有取值的对象集为NAir，在属性ai的相关属性上都有取值的对象集为RAir，含有空值的属性集为MAr，具体算法如下：

步骤1首先计算不完备信息系统的MAr、NAir、RAir；

步骤2计算各个属性间的相关性；

步骤3估算MAr中属性ai的空值，具体规则如下：

若在第r次迭代中ai的相关属性的取值没有发生变化，即的个数没有变化，则，其中，FIOWA为IOWA算子的聚合值；否则；

步骤4如果Sr已经为完备的信息系，则停止；否则令r=r+1，转至步骤1。

经过多次迭代之后得到的最终完备信息集Sr即为完备空战决策信息表。

3 基于直觉模糊集动态空战威胁评估

3.1 动态空战多目标属性权重的确定

对空战信息决策数据表补齐之后，运用直觉模糊熵权法确定目标属性的客观权重，并结合主观权重确定目标属性权重；采用泊松分布法确定空战时间序列权重；通过属性权重和时间序列权重来衡量不同目标属性和不同时间序列点的重要程度，具体步骤如下。

步骤1确定完整的目标属性动态直觉模糊决策矩阵

步骤2计算tk时刻目标属性直觉模糊熵

步骤3根据熵最小化原理建立目标属性权重的非线性规划模型

确定目标属性的客观权重后，并根据专家给出的目标属性主观权重sωj（tk），通过式（10）进行计算目标属性的权重ωj（tk），且αp表示主观权重的系数，αs表示客观权重的系数，满足。

3.2 动态空战多目标威胁排序步骤

采用TOPSIS方法的思想进行动态空战目标威胁评估排序，选取最新p个空战态势时间点，通过泊松分布法计算出时间序列权重的基础上，采用动态直觉模糊评估方法对空战多目标威胁评估解算，算法步骤如下：

步骤1根据已知的决策信息数据表，确定其各时间序列点的决策矩阵Q（tk），不计缺失数据；并根据计算的Q（tk）矩阵，构造填补矩阵：

步骤2采用IOWA算子的空值估计算法填补缺失数据；

步骤3确定目标属性的直觉模糊决策矩阵，见式（4）；结合专家给出的目标属性主观权重，通过式（7）确定各时间序列点目标属性权重；

步骤4计算tk时间序列点的加权直觉模糊决策矩阵 R（tk）及其正、负理想解；

步骤5计算tk时刻各目标xi到正、负理想解和的欧氏距离及相对贴近度ρi（tk），从而构造动态决策矩阵H；

步骤7确定加权动态决策矩阵K的正、负理想解K+、K-，计算各目标xi与动态决策矩阵的正、负理想解K+和K-的欧氏距离；

步骤8计算各目标威胁度Ci，并根据威胁度Ci的大小，对各目标进行威胁评估排序。

4 仿真及分析

某次空战中，我机遭遇3架敌机，敌我双方均在作战范围。取距离威胁因子参数k=0.7、l=0.2，角度威胁因子参数k=0.8、l=0.2，速度威胁因子参数e=0.7、c=0.3。我机机载设备所测信息如表2所示。

表2 目标各时刻属性信息

根据表1将空战能力语言变量值转换为直觉模糊集，根据式（2）～ 式（4）对距离、角度、速度定量属性进行直觉模糊化。

通过步骤1计算各时间序列点的决策矩阵Q（tk）（见表 3，t2、t3时刻计算方式与表 3 相同）。

根据空值估计算法进行填补缺失数据，对表3的填补信息见表4（此处只列出t1时刻），根据步骤3计算各时间序列点的目标属性权重 sω（tk）=（0.3，0.2，0.2）（见下页表 5），其中专家给出的主观权重；主、客观系数分别为0.4，0.6，再根据步骤4计算得到各时刻的加权直觉模糊矩阵（见表6）。

根据步骤4求R（tk）正负理想解，再由步骤5计算各目标xi与正理想解R+（tk）的相对贴近度ρi（tk），如表7所示。

根据步骤6，构造动态决策矩阵；

表3 t1时刻空战决策矩阵

表4 t1时刻目标属性的直觉模糊决策矩阵

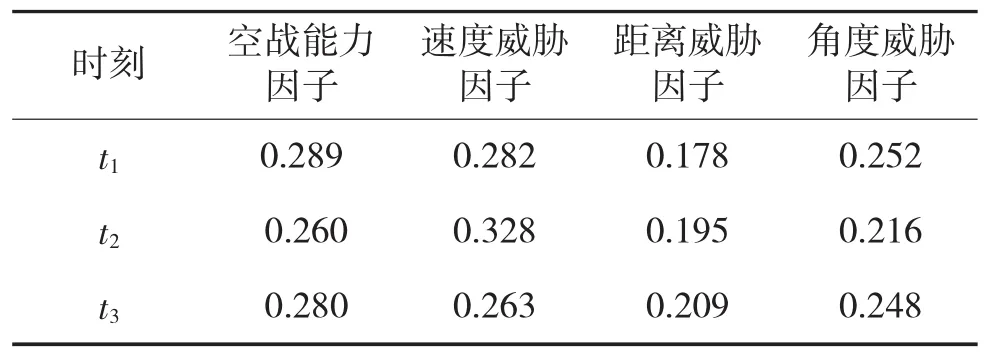
表5 各时间序列的目标属性权重

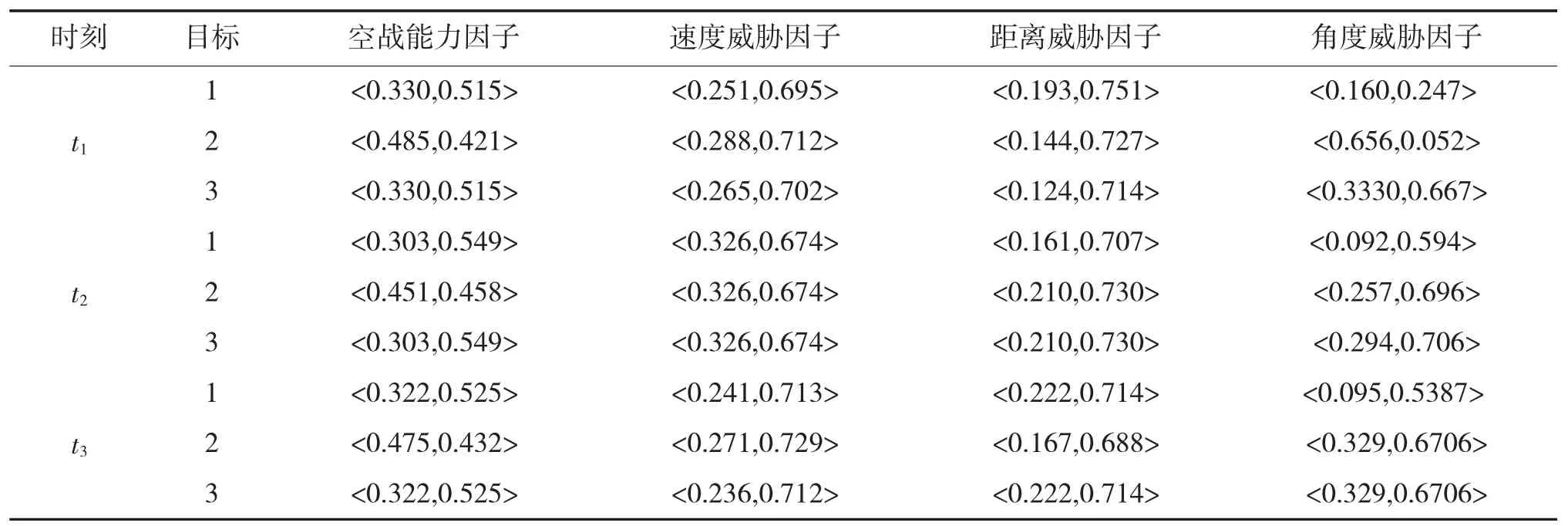
表6 各时刻加权直觉模糊决策矩阵

表7 各时间序列点各目标的相对贴近度

再由步骤7、步骤8依次计算可得各目标威胁度；

C=（0.506 1，0.536 9，0.529 0）

最终评估出的各目标威胁排序为：

目标2>目标3>目标1

在完备数据下，文献［10］在 t1、t2、t3时间序列点的目标威胁度分别为（0.607 7，0.630 8，0.621 3）、（0.627 0，0.627 8，0.623 6）、（0.616 6，0.649 3，0.627 5），综合各个时间序列点的威胁度值，可得威胁排序为：

目标2>目标3>目标1

与本文缺失数据下的威胁评估结果相一致，证明了该方法的合理性和有效性。

5 结论

针对现代空战环境下敌方威胁的多目标、动态性、不确定性等特点，提出了一种缺失数据下基于直觉模糊集的动态空战多目标威胁评估方法。将采用IOWA算子的空值估计算法思想运用到直觉模糊集理论中补齐缺失数据，并结合直觉模糊集相关理论对目标属性进行定性化与定量化的分析，运用直觉模糊集TOPSIS方法建立缺失数据下的动态空战威胁评估的数学模型，并通过仿真证明了该算法能够适应复杂、缺失数据场景下的空战威胁评估。