议高中物理力学解题中整体法的运用

周付豪

（山东省新泰市第一中学，山东新泰 271200）

1 整体法的基本概念

整体法指的是把多个受力的物体看作为一个整体，将他们相互之间产生的作用力看作为一个系统内整体的内在力，以及来对受力分析过程进行简化以及适当减少受力的分析对象。整体法是在高中物理学习中一种重要的解题思路、方法，与隔离法并列为高中物理力学研究的常用方法。由于力学的知识量庞大、知识难点众多因此需要借助整体法来抓住问题的主干思想，从而简化题目的难度，对其更好的提供帮助。

在运用整体法的时候，不能随便使用，应详细了解题意，明确其是否符合整体法的使用范围，再进行后续解题。

2 整体法在应用过程中的重要性分析

力学内容的篇幅较长，也是历年考试的重要考查点，虽然力学与生活息息相关，但是力是不可见的，很多学生在做题中不知道如何下手。所以在解题过程中，养成标记力点的习惯可以有效地降低遗漏的情况，可以使条理更加清晰，也便于自己进行后续整理。

整体法是将局部带入到整体的思维模式，主要作用可以将过程化难为简，将受力情况整体带入，避免出现受力点繁琐的情况也简化了解题思路，跳出题目给出的条框，从另一个角度看问题解决问题省略掉了很多繁琐的过程，极大程度上提高了学生的解题效率。很多学生要么不能正确分析受力情况，不明白如何下手解决，或者就是干扰项过多导致太过于繁琐，步骤越多越容易出错。而在学习过程中整体法的优点可以有以下几点概括。

（1）有效简化解题难度，提高解题效率。

（2）扩展物理问题，提高自身综合解题思路。

（3）从多方面分析问题，提高对物理教学内容的理解。

在解题过程中运用整体法，可以灵活地解决问题，在学习物理力学的过程中培养学生的整体性思维能力，从整体看待问题，不要太过于局限性。

3 整体法在解决高中物理实际问题时的具体应用分析

下面我们将通过相关的例题讲解，来更直观的展示整体法在高中物理力学问题的解题过程中的实际用处。

例一：将质量为M的斜面体水平放置于一粗糙表面上，斜面为光滑斜面，倾斜角为θ。现将一块质量为m的木块放置在斜面上，随着木块下滑的加速，试求在木块的下滑过程中，斜面体承受所承受的静摩擦力与支持力各为多少？

这种问题在物理学习过程中很常见，面对此类题目的时候，应该先对题目进行认真的审题之后再进行解题，题目给出斜面为光滑斜面，说明木块在滑动的过程中，可以暂且不考虑摩擦阻力，仅考虑重力作用，也给出斜面体角度为θ，设木块下滑加速度为a，a=gsinθ，公式中，g为重力加速度，所指出的加速度方面与斜面相平行，方向向下。

在解决这种问题的时候，如果逐个分析受力点会过于复杂化，使解题过程变得过于繁琐。可以通过整体法来对其进行解析，将木块与斜面看作一个整体，不去考虑其他的各种支持力与压力的存在，只考虑题中要求算出的摩擦力与地面的支持力，更简洁的完成整套题。

通过上述分析，可以得出算题步骤，求取斜面所受的摩擦力时，通过斜面受到的合力与木块的加速度，并结合牛顿的第二定律F=ma以及三角函数的关系式，可得出以下结论：Fx=macosθ=mgsinθcosθ， 简化后整理可得：f=magsin^2θ/2。

F=(M+m)g-N=masinθ=mgsin^2θ， 再简化后整理可得：N=（M+m）g-mgsin^2θ。

由此可见，整体法可以为解题过程很有效地提供更加简洁化的思路，从而提高学生的解题效率，以及学生的整体思维能力，但是之前也说过了，整体法并不是所有的题目都受用的，在实际应用过程中，不仅要掌握整体法的过程还应该对整体法的约束性更加了解，避免出现滥用的情况。

例：如图所示，将带＋q电荷量、质量为m的小球a与电荷量为-q的小球b，通过绝缘线将两个球球相连，并用绝缘线悬挂于房顶。房间内有强度为E、方向向左的电场，在这种情况之下，小球的状态为（）。

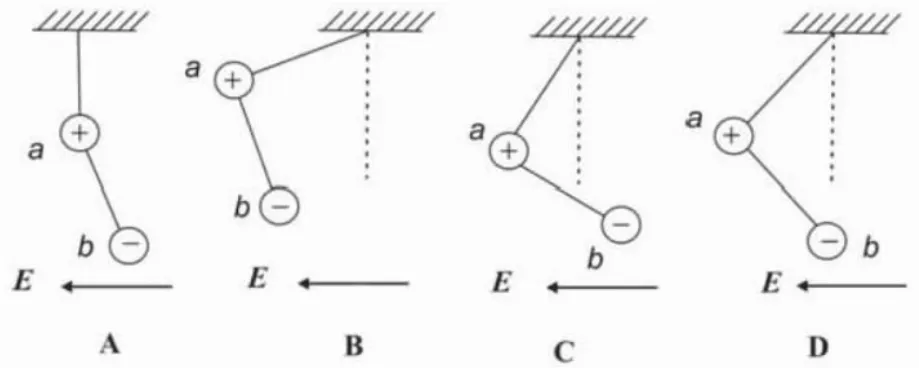
由题目可知，两个小球自身的所带电量是不相同的，如果采用整体法，将这两个小球看做一个整体，单方面的去进行受力分析就会直接的选择A项。但是题目给出两个小球的所携带电量的差异，电量不相同的前提之下，看成一个整体在进行受力分析时，左右电场的力是不能达成平衡的，也就是不可能为0，所以在排除A项之后，就是剩下的三个选项的区别就在于夹角大小的问题，将a球的细线与垂直方向的夹角设为α，这个时候再利用整体法来进行解题，把α与β看成一个整体，即为tanα=Eq/2mg,再回过来研究b球，将b球的细线与竖直方向的夹角设为β，即为tanβ=Eq/mg,所以有α＜β。即小球b与竖直方向大于小球a与竖直线间的夹角。所以这道题目选择C。

由上面两道题可以看出来，当整体水平稳定且一致，并且各物体系统内相互不涉及的情况之下，可以选择使用整体法来进行解题，但若整体状态不稳定、各物体之间的相互作用不清楚的时候也可使用整体法，不过什么时候，哪个步骤使用需要结合题目给出的条件，以及解题过程中的条件，谨慎使用，再进行后续步骤。

4 结语

综上所述，整体法的正确使用确实会为物理力学的解题带来很多便利之处，省去了极为繁琐的步骤的同时也减少了做题的出错率。不过更紧要的是需要仔细地对题目进行阅读，以达到理解的程度。在选择时使用整体法，将多元化的思维方式进行整合，使相互联系、相互制约、相互依赖的多个组成融合为一个整体。恰当地使用整体法可以有效地提升学生的做题思路，培养学生整体性思维模式，提高学生对物理学的积极性。